by Mary Hrovat

In the shapeless but often suggestive scatter of stars across a dark night sky, humans have picked out patterns and woven countless tales around them, giving the brighter stars names for their place in these stories. The star names we use today can be fascinating but also baffling—which is not surprising, considering that they’ve evolved over centuries in various languages.
Most of the traditional star names known to Western science have Arabic, Greek, or Latin roots. Some of these names have fairly straightforward meanings, although the connections are not always obvious. Orange-red Antares, for example, is named for its resemblance to Mars (the name can be translated as rival of Mars). Regulus means little king; the star has long been associated with royalty, and it’s in the constellation Leo, the lion (king of the beasts). Spica is the brightest star in the constellation Virgo (the maiden); its name is derived from a Latin term for an ear of wheat, because of the constellation’s identification with a Greco-Roman goddess of agriculture. It has been identified with many other female deities over time.
There’s also a star in Virgo named Vindemiatrix, which translates from the Latin as grape gatherer, because in classical times, when it was named, the Sun was in Virgo during the grape harvest. A star in Lyra (the lyre) is named Sulaphat, which is derived from an Arabic word for tortoise. It puzzled me to learn this; the reason is that lyres were often made from tortoise shells. The name of Arcturus, in the constellation Boötes (the herdsman), is derived from a Greek term meaning guardian of the bear, for several possible reasons involving myths about bears. Read more »

 Sughra Raza. Self Portrait in Early Summer, May 2024.
Sughra Raza. Self Portrait in Early Summer, May 2024.


 In 1762, Jean-Jacques Rousseau prophetically declared that “we badly need someone to teach us the art of learning with difficulty.” Two hundred and fifty years later, Rousseau’s words seem clairvoyant in their relevancy to schooling in the United States. Education has come to the forefront of the array of issues emerging in the post-Covid era. The abandonment of the alphabet soup of standardized tests, student reliance on Chat GPT, and rampant grade inflation all point to a wider problem. And though some politicians see the Ten Commandments as the solution to classroom troubles, universal progress toward a real solution seems far away. Not that some don’t try.
In 1762, Jean-Jacques Rousseau prophetically declared that “we badly need someone to teach us the art of learning with difficulty.” Two hundred and fifty years later, Rousseau’s words seem clairvoyant in their relevancy to schooling in the United States. Education has come to the forefront of the array of issues emerging in the post-Covid era. The abandonment of the alphabet soup of standardized tests, student reliance on Chat GPT, and rampant grade inflation all point to a wider problem. And though some politicians see the Ten Commandments as the solution to classroom troubles, universal progress toward a real solution seems far away. Not that some don’t try.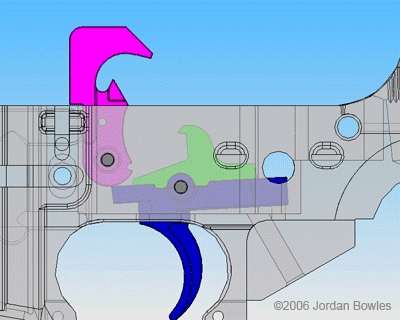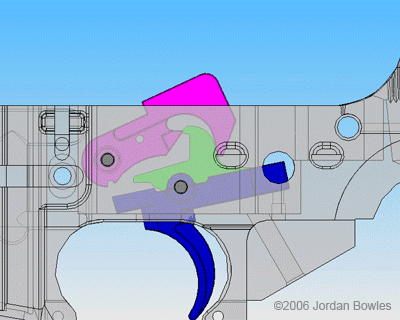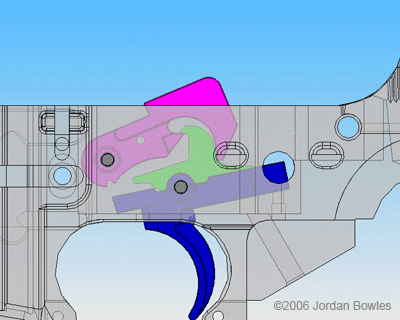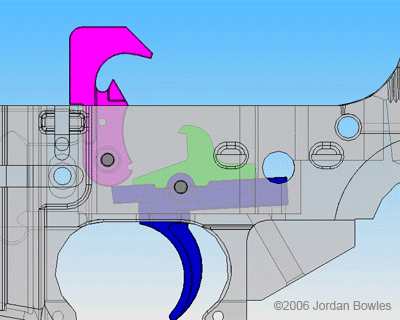



 Sanford Biggers. Transition, 2018.
Sanford Biggers. Transition, 2018. Have you ever read a book that you thought you were going to write? A book that captures something you’ve experienced and wanted to put into words, only to realize that someone else has already done it? The Apartment by Greg Baxter is that book for me.
Have you ever read a book that you thought you were going to write? A book that captures something you’ve experienced and wanted to put into words, only to realize that someone else has already done it? The Apartment by Greg Baxter is that book for me.


