by Jonathan Kujawa

Four years ago was peak COVID-19. I was thinking about moving furniture, which led to this essay here at 3QD. The topic was the problem of moving a sofa down a hallway with a 90° corner:

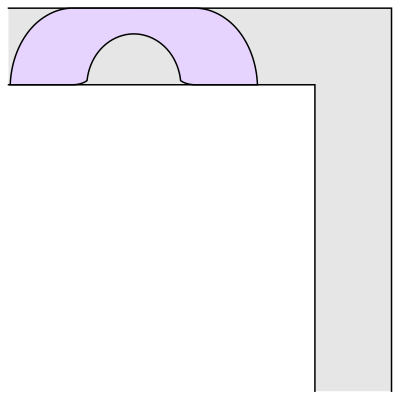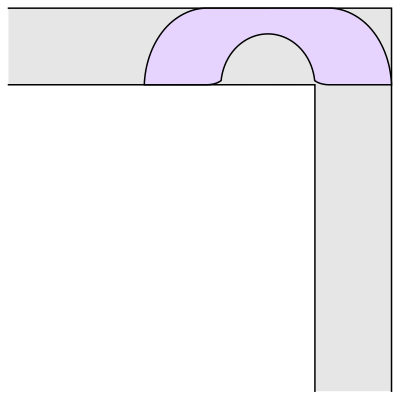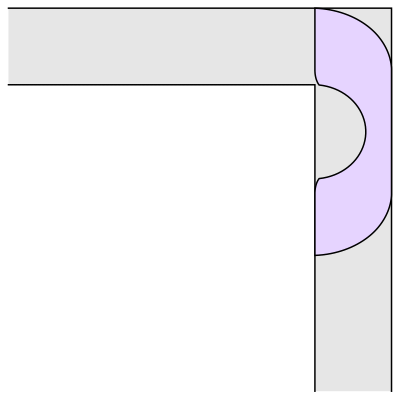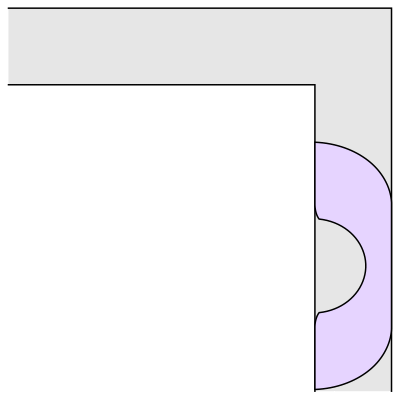
The problem is to find the “couch” of largest possible area that could be smoothly pushed down the hallway, around the corner, and then onwards. Leo Moser first asked this question in 1966 [1]. The image above is the couch found by Joseph Gerver in 1992. Gerver’s couch has an area of approximately 2.2195 square meters (where the hallway is exactly 1 meter wide).

As we talked about in that essay four years ago, Gerver used some clever math to find the shape of his couch. If you look very closely, you’ll notice that the corners are clipped off, and the inner semi-circle isn’t exactly a semi-circle. Without those tweaks, you have Hammersley’s couch from 1968, which has an area of π/2 + 2/π ≈ 2.2074 square meters. Several decades of time and Gerver’s hard work got us a whopping 0.0121 square meters.

Of course there was no guarantee that Gerver’s couch was the biggest possible. Dr. Gerver’s approach made no promises that it gave the best possible, after all. A little more convincing is the fact that in 30 years we haven’t been able to do any better. But mathematics is a game of centuries and millennia — a few decades is small potatoes. In 2018, Yoav Kallus and Dan Romik proved that the couch could be no larger than 2.37 square meters. But the gap in size between Gerver’s couch and the Kallus-Romik upper bound is an order of magnitude larger than that between the couches of Gerver and Hammersley.

I’m not an expert in this area, but if you asked me a month ago, I would have said it could be many years before we’d resolve Moser’s couch question. Indeed, this could easily be out of reach forever. Many easy-to-state math questions are practically unsolvable. One could make infinitely many tweaks to Gerver’s couch as possible improvements. Or, you could do some entirely different shape, maybe something fractally and totally unexpected.

Part of the problem is that there is no single formula that gives you the area of all possible couches. If you had such a formula, you could try to maximize its output like you learned to do in your Calculus class. But if different shapes have different area formulas, there is no effective way to tackle them all at once.

This is no doubt my own human biases, but I find it a big bummer that Hammersley’s couch with an area given by a beautiful formula using pi is not the maximum. Once you show me that tweaks can give you bigger couches with ugly areas like Gerver’s, my hope for a definitive answer pretty quickly disappears.

So I was gobsmacked to see two interesting papers about Moser’s couch problem in the last few weeks. Read more »

by Paul Braterman

Tim LaHaye’s career shows a direct line of descent within creationist thinking, from Reagan-era anti-Communism, through a more diffuse blanket opposition to humanist thinking, to American exceptionalism and the impulses that would later express themselves in 21^st-century Christian Nationalism.

LaHaye gives us a bridge between traditional morality, anti-Communism and Reaganism, and present-day Christian Conservatism, with humanism having taken the place of Communism. His claim that evil humanists had successfully conspired to take over the American power structure is echoed in today’s denunciation of the “deep state,” the end-of-the world thinking of his highly successful Left Behind novels underlies much of the religion-linked opposition to action on climate change, and his rejection as satanic of every idea that he regards as unbiblical now surfaces as anti-wokeism, along with opposition to examining America’s racist past and to the teaching of evolution.

Add to this his lamenting a morally superior past, his claim that American exceptionalism is biblical, along with capitalism, and his appeal to moral patriotic Americans (he repeatedly links those adjectives in his writing) to take back the country from the forces of evil, and we have a direct link to the doctrines of evangelical Trumpism. His claims that the US constitution is Bible-based, that the US “was founded on a basic consensus of Christian principles – more so than any nation in history,” and that the division of powers was inspired by a biblical awareness of the fallen nature of man, fall short of more recent assertions that the constitution itself was divinely inspired, but nonetheless point the way to the explicit Christian Nationalism now about to assume power.

LaHaye graduated in 1950 from Bob Jones University, then as now strictly six-day creationist and socially conservative, and later became pastor of Scott Memorial Baptist Church (a.k.a. Shadow Mountain), in the suburbs of San Diego. Here he served for 25 years, developing the church into a megachurch, while embarking with his wife on a broadcasting career, offering family advice from their socially conservative Christian perspective. In the 1960s he committed himself to anti-communism, joining the John Birch Society. He was also powerfully influenced, as were many other creationists in his generation, by the philosopher Francis Schaeffer, who regarded faith as absolute, Genesis 1 – 11 as foundational to our knowledge of space and time, and all secular thinking that ignored this foundation as misguided. Read more »

by Ed Simon

The twentieth-century Russian critic Mikhail Bakhtin’s concept of the “chronotope” is among the more enigmatic concepts in literary theory, a discipline not defined by a deficit of them. In his 1937 essay “Forms of Time in and of the Chronotope in the Novel,” later published in his seminal collection The Dialogic Imagination, Bakhtin writes of his eponymous neologism that it involves the “intrinsic connectedness of temporal and spatial relationships that are artistically expressed in literature,” consciously drawing from Einstein’s discovery of space-time in a manner that’s metaphorical, but as the critic makes clear, “not entirely.”

What Bakhtin is getting at, in a manner that may seem esoteric but is estimably useful, is that in a given work of literature, space and time are not separatable, but inextricably connected, and that furthermore a particular relationship between those two qualities – that is a particular chronotope – is what defines specific literary genres. Within a given chronotope, “spatial and temporal indicators are fused into one carefully thought out, concrete whole,” writes Bakhtin, “Time… thickens, takes on flesh, becomes artistically visible; likewise, space becomes charged and responsive to the movements of time, plot and history.”

This year I tried to read as many examples of Bakhtin’s favored form of the novel as I could, and as always I didn’t go into my casual reading with a preordained theme in mind, but perhaps because of the exigencies of our current historical moment, many of the works on my list this year were obsessed with time, with thickness and fleshiness, and how that temporality connects to space. Novels took place in the past, present, and future, in alternate histories and as kaleidoscopic nesting narratives, but throughout those that impressed upon me the most urgency there was a distinct sense of the chronotope, of how fiction is a form of time travel. Read more »

by Tim Sommers

Where you are, death is not. Where death is, you are not. What is it that you fear? –Epicurus

I knew I was in trouble as soon as I saw them. They were driving one of those huge pickups with four back wheels instead of two – what I now know is called a “dually” – and they kept drifting to the side of the road, hitting the rumble strip, and then jerking back into their lane.

It was early June, Old Mine Road just east of Litchfield, Illinois, late on a Friday. I was working as a courier out of St. Louis and I had just completed my last run of the week, intravenous medication for a little girl on a farm, one of those runs that makes you feel okay about what you do, and I was heading back to St. Louis.

It was a clear evening so I could see these guys from way off, drifting then jerking, drifting then jerking. The problem, my problem it turns out, was that this was a two-lane road with a sixty-mile-an-hour speed limit, no shoulder, and the roadbed was raised about four feet or so above soybean fields on either side. Furthermore, we were coming up on a stretch of road hemmed in on both sides by guardrails. I actually considered driving off the road to avoid them. I pictured my conversation with my insurance agent not going well, though.

I slowed a little and drove between the guardrails. They drifted again and hit the nub end of the guardrail head-on. The back of their truck rose into the air and all four back wheels came off and spread out across the highway like hellfire missiles. I sped up a little and managed to drive under a tire coming straight at my windshield, then I hugged the guardrail as tightly as I could, but the truck was upside down now sliding across the pavement on its roof, sparks flying, and I was out of room.

(A policeman who interviewed me a few hours later, even before it was clear whether I would live or not, insisted the truck was not upside down. “People don’t remember things after trauma like that.” I said, “Why are you talking to me then?”)

Then it hit me.

Every pane of glass in the car exploded at once, my airbag deployed, and the car went through the guard rail becoming airborne and knocking a four-by-four post into the air so that it spun in front of the windshield like a helicopter rotor. As soon as I saw it, I thought, “That’s going to come through the windshield and hit me in the face.” Then it came through the windshield and hit me in the face. Read more »

by Varun Gauri

I suppose proud Indians are all alike, but every American-born, confused desi is confused in their own way.

The Ohio hills reminded me of the snow-capped Himalayas. Not that I’d seen the Himalayas. I had seen a documentary about the heroism of Sir Edmund Hillary and Sherpa Tenzing Norgay, the dynamic duo who first scaled the Everest summit (it was about Hillary’s heroism, mostly). Then a storm dumped over a foot of snow on Cleveland in January 1978, on top of the two or three feet already on the ground, and 80-mile-per-hour winds kicked up six- and seven-foot snow drifts along my newspaper route. I completed my deliveries, nonetheless, returning home, cold and frost-bitten, by 8 am. Obviously, Sir Edmund and Sherpa Tenzing wouldn’t have been deterred, either.

Another childhood hero was my mail order guru, Paramahansa Yogananda. I fell for him because, unlike the other mystical outfits I wrote to, his Self-Realization Fellowship accepted thirteen-year-olds. Also, Guri-ji and I had the same birthday. I started meditating on a metal folding chair covered with a white blanket, in my bedroom closet, because the Fellowship recommended insulating yourself from worldly currents. I continued to be a committed, avid disciple throughout my teenage years, even maintaining my practice at a high school summer program at Cornell University. My roommate Marc, from Dallas, was startled when, opening our dorm-room closet to grab a pair of his shoes, he found me seated on a blanketed chair, palms upturned on my knees. Marc and I later had a productive conversation about the cultural differences between Texas and Ohio.

At home, behind my bed, I mounted a glimmering handloom tapestry from rural Rajasthan. For a costume party cum talent show, I had dressed up in a saffron loincloth, with a trident staff and an alms bowl for props (plus some random forehead markings). I watched the Gandhi biopic three times, learned the basic cricket rules, read the Bhagavad Gita, fasted on fruit and nuts on Tuesdays, and ate pungent okra-in-chapati sandwiches at lunch in the school cafeteria.

I was on Team India. To be a fan is to celebrate your team’s wins as your own, and I felt honored that my country had apparently invented the number zero. Indians had built glorious temples, palaces, and ancient cities with impressive feats of engineering. “We” made major contributions to logic, philosophy, linguistics, and religion. Gandhi was the most significant figure of the 20^th century. Yoga was taking off everywhere. These were vicarious victories, as when your team receives multiple All-Star selections. Read more »

Walked by a small truck with a bit of snow and ice on its windscreen, and this reflection of a tree.

Enjoying the content on 3QD? Help keep us going by donating now.

by Brooks Riley

Enjoying the content on 3QD? Help keep us going by donating now.

by Nils Peterson

Santa, A Better Understanding

The Christmas song we all know has got it all wrong. “Better watch out, Better not cry, Better not pout, I’m telling you why, Santa Claus is coming to town.” This turns his gifts into a payoff. You do this and you’ll get that. It’s salary. But a gift isn’t salary. A gift is like grace, something you are given, not something you have earned or deserve. That’s where the real Santa comes in. He wants to give you something because you’re part of creation and you’re you. Indeed, the creation is one of his gifts.

CFO’s have taken over Christmas and tried to make a gift part of their accounting department. Their carrot and stick: if you don’t act right you won’t get gifts. The sense is that if you aren’t deserving, deserving meaning acting the way they think you should act, you won’t get anything, or, maybe, a lump of coal in your stocking while sister gets an orange. But Santa is better than that. The world is better than that.

Christmas Mysteries

Christmas morning. I wake early
to a strange noise from below,
and, in my footed pajamas, holding
on to the railing, I creep down the
shadowy stairs leading from the
chauffeur’s flat to the workroom
below. Of all things, there’s my
father bending over an electric train
whizzing round and round an oval
track nailed to a piece of plywood.
He doesn’t see me, but I watch him
caught as he is in the mystery of train
lights, ruby and white, circling in
the half-darkness. For awhile I don’t
make a sound, but watch him,
wondering about his strange smile.

All these years later, I tiptoe down
the stairs again, now understanding
the poverty of his childhood
and the jobless years of the Depression,
and I watch him and imagine him thinking –
I am able
to give to my children,
for Christmas,
this wonder.

P.S. The song, though it doesn’t know it, has one line we need to appreciate – “So be good for goodness sake.” Think about it. N

A Wish for the New Year

the year is a road
that turns on its way
where we are seems clear
and maybe next day
but then in its going
it bends out of sight
we follow its flowing
with all our unknowing – NP

“Ye shall have a song … and gladness of heart.”

The thought comes from Isaiah, “Ye shall have a song, as in the night when a holy solemnity is kept; and gladness of heart, as when one goeth with a pipe to come into the mountains of the Lord.”

So not only a song, but a particular kind of song – an “as in the night when a holy solemnity is kept” kind of song, not only gladness, but a particular kind of gladness – an “as when one goeth with a pipe” kind of gladness. And if you “goeth” you must be heading somewhere. The text says, “to come into the mountains of the Lord.” Wherever you find your “mountains of the Lord,” you’d want go there carried by the joy of your own music.

I first met this verse more than 70 years ago singing Randall Thompson’s Peaceable Kingdom with my old college choir. I can close my eyes and sing it again with my friends, auld lang syne indeed. And remembering further, here’s the text of almost the penultimate song of that piece, also from Isaiah, “The paper reeds by the brooks, by the mouth of the brooks, and everything sown by the brooks, shall wither, be driven away, and be no more.” It too is a marvelous in its dark, descending chords and thoughts. Wonderful music to sing, but “Ye shall have a song and gladness of heart” answers the darkness with a fine antiphonal eight-part chorale full of joy and gladness, gladness of heart. Isn’t that the best gladness? “Gladness of heart.”

My New Year’s Wish for Us All, “Ye shall have a song … and gladness of heart,” No, I should say “We shall have a song…and gladness of heart.”

A New Year’s Question. Coleman Barks in his book The Scrapwood Man asks “I would like to know what you have escaped, how you slipped free from some compulsion or inherited condition. What moved your story along?”

“What moved your story along?” A great question to ask at the beginning of a new year and to think about now and again as the year winds on its way.

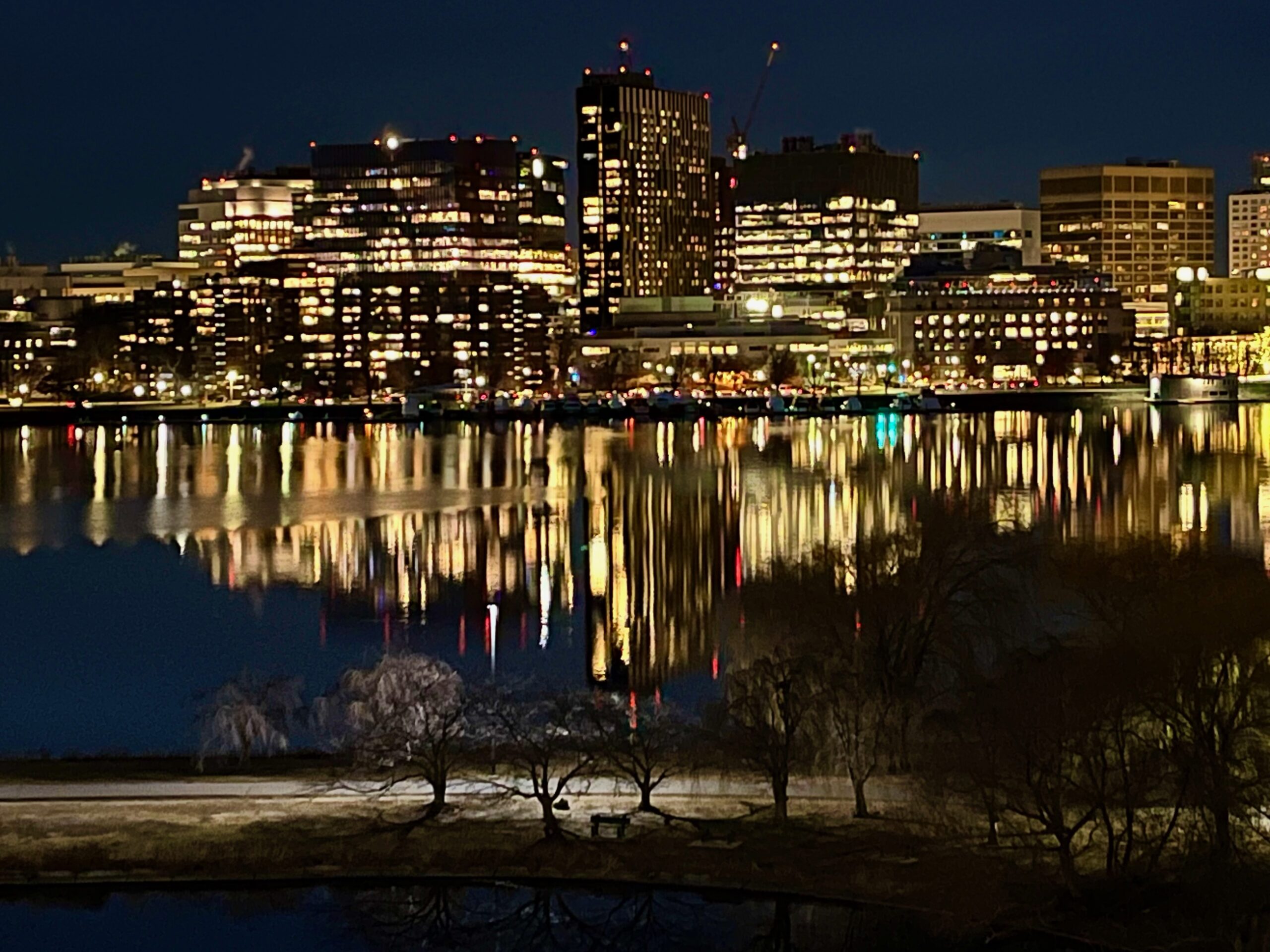Sughra Raza. Cambridge In The Charles, December, 2024.

Digital photograph.

Enjoying the content on 3QD? Help keep us going by donating now.

by Azadeh Amirsadri

I will be in Strasbourg, France during Christmas this year, spending time with my 96 year old father who talks about his mother, my mother, and his cousins, all gone now, but seemingly alive to him.  Strasbourg, as beautiful a city as it is, has always been a bittersweet place for me, from my childhood when I went to kindergarten there until now. Good and bad memories merge in a city known for its gothic cathedral, Christmas market, Rhine Valley wine, and specialty cuisine.

I lived in Strasbourg from the age of six to nine, and that was the first time I experienced Christmas. There was a woman, Mademoiselle Simone, who worked in my  younger sister’s preschool that my parents had befriended. She would visit us in our home or she would have us over at her parents’ house, where they showed us a porcelain cup that had a bullet hole in it from the second world war, or maybe the cup is something I created in my mind. One year, she took us to the beautiful Cathedral of Notre Dame in Strasbourg for Christmas Eve. I don’t remember my parents being there with us, because we had that no-parents-around energy and we felt special to be there with her. I remember a lot of people inside and outside the huge cathedral, and worrying about getting lost in that crowd as she told us to hold hands. I also remember the lights, candles and music, and sweet Mademoiselle Simone who gave us each chocolate and an orange.

We went back to Iran when I was nine years old, and I secretly liked Christmas and envied anyone who was lucky enough to be in a family that celebrated it. I had two Christian friends in school, both Assyrians, who put up Christmas trees at their house. I would go over and admire their green trees with silver garlands, red ornaments, and a star or angel on top. A few pop-up stores sold fresh trees and tall red statues of Santa Claus, or Baba Noel as we called it. It all looked so magical to me and I envied my friends’ holiday that was special to them only. I also loved Nowruz, the Iranian New Year, but everyone got to celebrate it which made it not as special as Christmas in my preteen mind. Read more »

If you talk about it, it’s not Tao
If you name it, it’s something else
What can’t be named is eternal
Naming splits the eternal to smithereens
………………… —per Lao Tzu, poet, 6th Century BC
_____________________________________

Lao Tzu’s Lament

At first I think, I’ve got it!
Then I think, oh no, that’s not it.
I think, it’s more like a flaming arrow
shot into the marrow
of the bony part of everything,
………. but some summer nights
………. it’s hanging overhead so bright

Then right there I lose it,
let geometry and time confuse it,
then it’s silent, it won’t sing a thing,
………. but some summer nights
………. it’s croaking from a pond so right

Then again, I lose it,
let theology and time confuse it,
then it’s silent and won’t sing a thing

………. I’m thinking I’ve been here before
………. feet two inches off the floor,
………. thinking, is this something true?

Sometimes I think I’ve lost it,
though I never could exhaust it
because it’s lower than low is,
and wider than wide is,
deeper than deep is,
higher than high is,
….……. but some fresh spring days
……….. it’s cuttin’ through the fog and the haze

I’m thinking I’ve been here before,
feet two inches off the floor, thinking

is this something true?

Jim Culleny, 7/15/15
Song rendition here: https://soundcloud.com/jim-culleny/lao-tzus-lament

Enjoying the content on 3QD? Help keep us going by donating now.

by Mike Bendzela

During the twelve years I was a volunteer Emergency Medical Technician-Basic in my little town, I arrived onto scenes with patients suffering varying degrees of distress. I would first assess them, then help stabilize and package them for transport to the hospital; and if I was lucky, I would be assigned to drive the ambulance. It wasn’t that I minded assisting paramedics in the back with “bagging” (ventilating) critical patients or performing chest compressions on them; it was just that when the rig was rocking Code 3 on the way to the hospital, I was in danger of throwing up all over the floor in back. The medical term for this is kinetosis.

In those years I got to witness a fascinating phenomenon in a few patients who had suffered blunt force trauma to the head. Some patients who had not been rendered unconscious, and who were not so severely injured as to be completely incapacitated, existed, for a brief time, in a little window of reprieve–a period of grace, as it were.

Following trauma, a patient’s sympathetic nervous system fires up; the body is flooded with hormones such as adrenaline, and the capacity to feel pain diminishes. Most non-essential bodily functions are temporarily suspended, but the mind exists in a state of both intense excitation and preternatural calm. Perhaps this is a survival mechanism, evolution’s way of allowing an animal to keep its wits about itself long enough to crawl out of further harm’s way.

Our crew was called along with the sheriff to the scene of an adult male who had been bludgeoned with a baseball bat in bed by his wife, to whom he had served divorce papers. She then shot herself in the stomach with a revolver and called 9-1-1, claiming an intruder had attacked them. (Much of the background of this call came to us only weeks later.)

By the time we arrived, the wife-assailant was being treated by another crew, and our patient was sitting up on the edge of his bed, bloodied but conscious. He sat there quietly, leaning one elbow on his knee, the other arm cocked on his hip, and he looked at us with his head tipped to one side, as if listening to some music in the background. Read more »

by Mindy Clegg

Since the 2024 election, liberals, progressives, and the left has been wringing our collective hands over why Trump won yet again. Was it the racism, the misogyny, or the economy stupid? Was there some fraud happening behind the scenes? Was the Democratic party “too woke” or not “woke enough”? Did the Democrats ignore the common clay of the new west in favor of “they/them”? Did they lose the propaganda war? Was it people not voting or was it people voting, but against them? Do we blame white men, white women, Black men, Latinx voters or those who did not vote at all? Endlessly, on and on. Partisans of each explanation insist that they have the only real answer to the question of why Trump. But I would say that rather than singling out one reason as the answer, there are grains of truth in each.

Yes, people are struggling, even as the economy has been doing well. Yes, people did not vote for the obviously more qualified Black/South Asian woman because of misogyny and racism. Yes, the democratic party can be out of touch. Yes and more. History tells us that rarely is a single answer satisfactory in explaining events like this. But another I have not really seen is what role does nihilism play in the recent election. We know that trust in our shared institutions are at an all-time low across political divisions. While the roots of that are in the failures of those institutions, culture—especially culture lacking in political specificity but that positions itself as outside the mainstream—drove a commodified version of rebellion against our institutions. You can especially see this with the rise of “alternative” culture in the 1980s and 1990s. As such, Generation X took away a specifically nihilistic message that often provided no strong political sentiment. Many white Gen Xers seemed to have carried that worldview into the politics today, preferring a bomb thrower to political problem solver. That bomb thrower was seen as being more authentic, despite his obvious history of lying. Read more »

by Daniel Shotkin

This week, electors from across the country will cast their votes for the next president of the United States. Only now, more than a month after Election Day, will Uncle Sam officially wave goodbye to election season. That seasonal bout of incessant campaign mail and debate fever has found its way off the front pages, replaced by a national rumination over one question: How did we get here?

The overarching answer is that it depends on who you ask. The self-assured economist will tell you that Donald Trump’s election is simply the result of widespread dissatisfaction with inflation—“it’s the economy, stupid.” The zealous Middle East correspondent will point to Kamala Harris’ support of Israel’s actions in Gaza. The MAGA Evangelical will tell you Trump’s win was the direct result of divine intervention. As a poll worker, I have a slightly different take on the election. Instead of focusing on the results, I think we can learn more about the state of America in 2024 from Election Day itself.

To preface, I am not the most typical poll worker. As a high school senior, I signed up to work the polls through a program my school offered with the local town. Eight hours of light work with my friends for $200 was a great deal, especially since we would skip school. But the gravity of this particular gig hit full force during the mandatory four-hour training in our cafeteria—our instructor informed us that “our nation and democracy depend on you.” Quite a lot to ask of forty-odd chattering high school students.

By midday on November 5th, I walked to my assigned polling station unsure of what to expect. I had heard stories of election workers being threatened in battleground states, though I was skeptical of that happening in suburban New Jersey. Our instructor had also warned us to expect “challengers”—party officials inspecting voting procedure—watching our every move. After months of end-all, be-all election coverage, the only thing I felt sure of was that this election, more than any other, would be exceptional. My suspicions were confirmed as the polling station came into view. Read more »

by Mary Hrovat

It sounds like a parlor trick or gimmick, to walk 2,024 miles in 2024—trivial but harmless. It’s not like hiking the Appalachian or Pacific Crest Trail or climbing the highest peak on each continent, or running a marathon. But it is similar to a marathon in that the number involved is an arbitrary product of history that can somehow be useful for guiding a person’s efforts.

The idea came from a friend. Early in 2020, I mentioned that I’d walked 1,929 miles in 2019, and he suggested that maybe I could walk 2,020 miles in 2020. Adding just under 100 miles, which is less than 2 miles a week, certainly seemed well within my capacity. I sold my car in 2018 and have many reasons to go for a walk. However, I didn’t manage 2,020 miles in 2020, and I couldn’t increase my mileage significantly in subsequent years either, until now. As of this writing (December 14), I’ve walked 2,079 miles. I passed my target a week ago, on a Saturday morning when I walked a couple of loops in my neighborhood to catch some rare December sun and get my day off to a good start.

∞

The years of thinking about my goal but not achieving it had clarified for me the seasonal patterns in my walking: I tend to walk less in summer, when the heat makes it uncomfortable to be outside, and sometimes less in winter if it’s icy or extremely cold. I walk less when I’m held immobile by depression. I usually feel better when I walk, but sometimes I get so far down that it’s hard to leave the house. That’s part of what happened to me in 2020.

In 2020–2023, I noticed that I kept on track toward a number of miles that matched the year fairly well up until about May. After that, I slowly got so far behind that it became impossible to catch up. This year, I thought I’d keep a spreadsheet so that I’d be more aware of how I was doing. I set up one that showed my running total, by week and by month, and how far off I was from my target for each week and month in the year. Read more »

Water flowing over rocks in the river Eisack in Franzensfeste, South Tyrol.

Enjoying the content on 3QD? Help keep us going by donating now.

by Rachel Robison-Greene

I’ll never forget the moment when it dawned on me that I had arrived at middle age. I caught a glimpse of myself in the mirror. Nothing much had changed—my eyes were the same distance apart. My nose was in the same place. My grey hairs were still mostly hidden in my ample mane. What was suddenly different was how I interpreted my self.

I poured through my selfies on my iPhone with the intensity of Narcissus gazing at his image in a pool. Had I, just now, interpreted myself correctly for the first time in years? Had I somehow misunderstood myself until now in ways I should have found humiliating? Who is my “self” and who gets to determine who has it right?

It’s common to convey this general line of inquiry as a set of persistence questions. What is it, if it is anything at all, that allows a thing or a person to remain the same thing or person through time and change? Is a ship the same if its planks are replaced and what has become of the marble when it is carved into a statue—that kind of stuff. Less abstractly but more painfully, it is an existential question: how can I keep my grasp on sanity when the locus of my frame of reference and the source of my motivation shifts like sand? In youth, our sense of self is awkward and underdeveloped but also vibrant and life affirming. Part of the difficulty of aging is the recognition that the self is mortal, contingent, and unstable.

Consider popular expressions involving the self: “I wasn’t myself today,” “Control yourself,” “Keep it to yourself,” “know yourself.” These expressions don’t exhort us to be sure to persist through time and change; they press us to be cognizant of something else, something more fundamentally personal. Our selves matter to us in a way that they don’t—and can’t—matter to rocks, plants, or snails. Doorknobs aren’t concerned with whether the version of themselves they’re projecting to others is one with which they will be comfortable when they go to bed at night.

Philosopher and neuroscientist Patricia Churchland argues that developing a sense of self was evolutionarily advantageous for humans. A creature that could recognize itself could understand itself as having a welfare—things could go well or poorly for it from its own point of view. Read more »

by Steve Szilagyi

The Naked Gun trilogy was a series of three film comedies released between 1988 and 1994. They were directed by David Zucker, who founded a new school of parody with his breakthrough movie, Airplane! (1980). Part of Zucker’s genius was casting grim-visaged actors from serious films and letting them loose in a perfectly silly universe. Leslie Nielsen, Lloyd Bridges, Kareem Abdul-Jabbar—he made some brilliant casting choices. He also made one grotesque error: O.J. Simpson.

Long ago, I interviewed Simpson for a publicity job and came away thinking that he was the greatest guy in the world. When the Naked Gun films came out, I laughed my head off. Simpson was in all three of them. He wasn’t much of an actor, but I thought he was a great sport to let Zucker use him as a slapstick stooge—just what I would expect from a super guy like Simpson.

Then came the murders of Nicole Brown and Ronald Goldman. After learning the details of that crime, I could never watch a Naked Gun film again. How could I? How could anyone laugh freely at a film that has the face of an atrocious killer in every shot?

Confronting Convergence.  Something like this happened to me on a recent visit to the Buffalo AKG Art Museum. Among the masterpieces in the museum’s collection is Jackson Pollock’s Convergence (1952), one of his classic drip paintings. My usual practice (and probably yours) when viewing a Pollock is to stand back for a few minutes to take it all in, then move in close and mentally merge with Pollock’s universe of speckles and swirls.

This is what I started to do with Convergence. But I couldn’t take that last step. Something was blocking me, and I knew exactly what it was: my recent reading of historian Henry Adams’ book Tom and Jack: The Intertwined Lives of Thomas Hart Benton and Jackson Pollock.

Adams’ book is a splendid dual biography, full of insights and revelations. What came back to me, however, as I stood in the Buffalo museum, was Adams’ account of August 11, 1956, the last day of Pollock’s life, and the painter’s role in the death of an innocent young woman. Read more »

by Brooks Riley

Enjoying the content on 3QD? Help keep us going by donating now.