by Jonathan Kujawa
“Odd,” agreed Reg. “I’ve certainly never come across any irreversible mathematics involving sofas. Could be a new field. Have you spoken to any spatial geometricians?” —Douglas Adams, “Dirk Gently’s Holistic Detective Agency”

It turns out mathematicians are well-adapted to working from home in the covid-19 pandemic. We don’t need research labs or access to original texts for our research, and teaching math over video chat is infinitely easier than art, music, literature, foreign languages, or practically any other subject. That said, mathematicians get cabin fever, too.
Recently, Anne and I have been talking about rearranging our offices here at home. In the past, they doubled as guest bedrooms and storage for exercise equipment and homeless plants. Which is fine if you’re using them for weekend afternoons and the occasional work-from-home day. But it’s six months in and time for our house to better match the present and foreseeable future.
Our first idea was to replace a guest bed in one office with a couch. Setting aside the difficulty of choosing a new couch sight unseen during a pandemic, there was the more practical problem of choosing one which could actually fit into our house.
Not long after we graduated from college, my childhood friend Troy spent months choosing a new sofa as part of a program to adultify his clothes, furniture, and life in general. He finally found the perfect one. After waiting weeks for it to be delivered from the manufacturer, it arrived but didn’t fit up the stairs of his apartment building. The delivery guys twisted, turned, lifted, shoved, and wrestled, but had no luck [1]. Sadly, it had to be returned and Troy was left despondent. Twenty plus years later, I’m pretty sure he would still defend that sofa as the finest, most comfortable couch ever made.
In our case, the house is ~70 years old (historic by Oklahoma standards), with narrow stairs, a tight turn at the top, and an even narrower doorway into the bedroom/office. After researching our options, and remembering Troy’s travails, we decided to go with a comfortable sitting chair for the time being. The couch is on the back-burner until the pandemic subsides and we better know what our long-term plans will be.
I’ve taken advantage of the lull in furniture moving to remind myself of the Sofa Moving Problem. In 1966 Leo Moser posed the following problem:
What is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width one?
That is, if you have a hallway of a fixed width, what is the largest sofa you can get around a ninety-degree corner? For example, if you have a square block that just fits in the hallway, you can slide it into the corner, then slide it down the other hallway. The block will necessarily have dimensions 1 x 1 and so have area 1. It’s not hard to see you can do better. For example, a semicircle of radius 1 will also go around the corner:
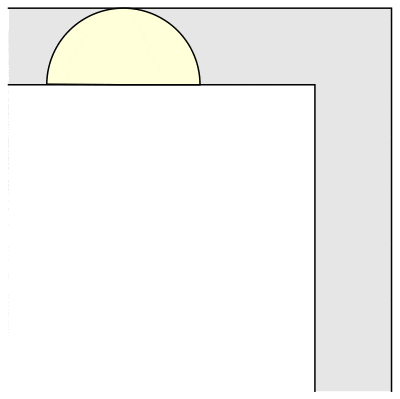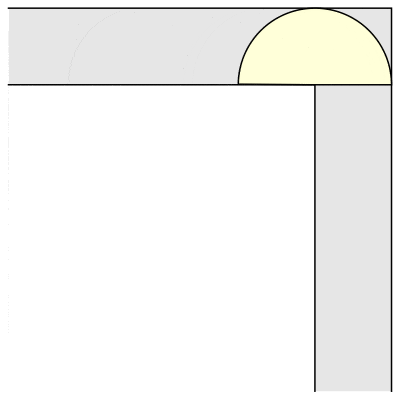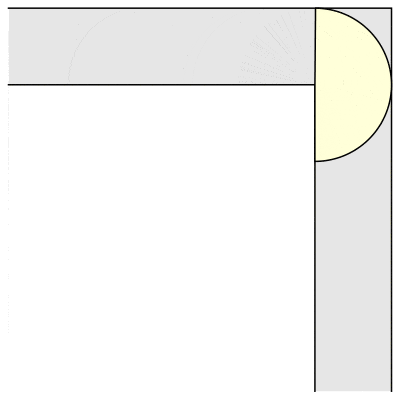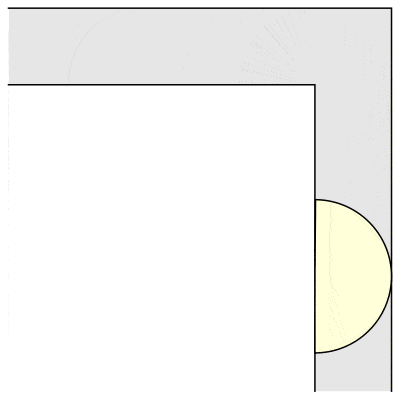
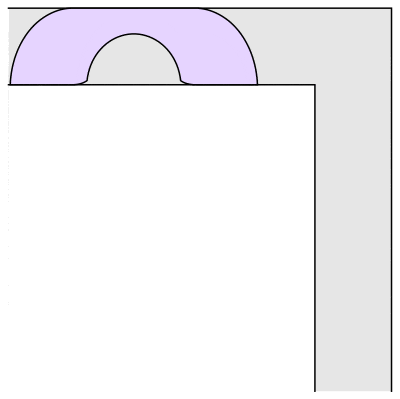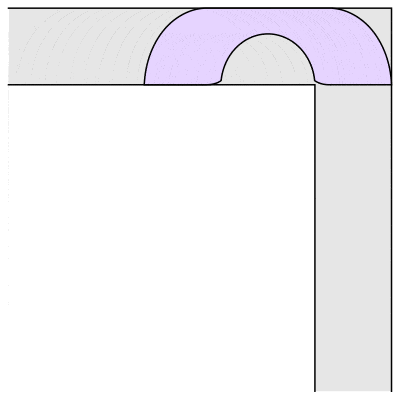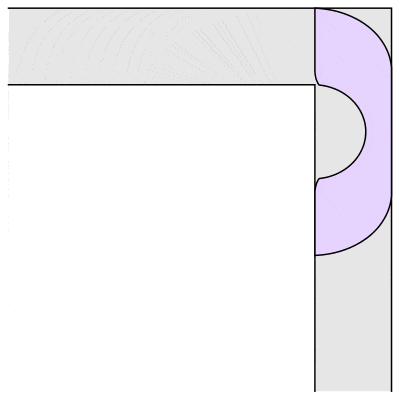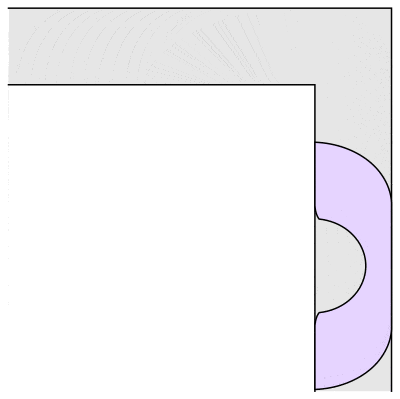
In fact, I lied just then. If you look closely at the animation of Hammersley’s sofa, you will see the corners have been rounded off. This innovation came from Joseph Gerver in 1992. Garver discovered that if you make Hammersley’s sofa, but with 18 different curves fitted together just so, then you could make it slightly larger and still fit around the corner. Gerver’s sofa as depicted above has area ≈ 2.22 square units.
Gerver found his sofa by assuming the sofa was made by a number of curve segments fitted together and expressed how the area would change if you made slight changes to the path of the sofa as it goes around the corner. This leads to a system of differential equations which can be solved to find the shape of the curve segments which give maximum area.
Gerver’s method doesn’t guarantee you’ve found the maximum area overall. For one, maybe there is some crazy shaped, fractal sofa which isn’t made up of nice curve segments. For another, Gerver’s approach assumes you can find an optimum by making small perturbations. It could be that the optimum is an isolated peak surrounded by much worse options. I’m not an expert, but it seems Gerver’s method might not find that solution.
That said, Gerver’s couch is still the best known. It remains an open problem to do better.
On the other side, you can ask for upper limits to what is possible. In 2018, Yoav Kallus and Dan Romik proved that the largest possible sofa which can fit around the corner is 2.37 square units. Their results show that Gerver’s sofa is awfully close to the best possible (or miles away, depending on your perspective!).
In fact, Kallus and Romik did even better. They designed a computer-based computational method and proved the longer you allow their SofaBounds program to run, the better your upper bound. Moreover, those shrinking bounds get arbitrarily close to the size of the optimal sofa [3]. If you implement their program and let it run long enough, you could break the world’s best estimate of the optimal sofa size.
Of course, mathematicians are never satisfied. John Conway and others asked for the maximum area of a sofa which has to navigate both right-handed and left-handed ninety-degree turns. Dan Romik used methods similar to Gerver’s and found the following peanut-shaped couch:
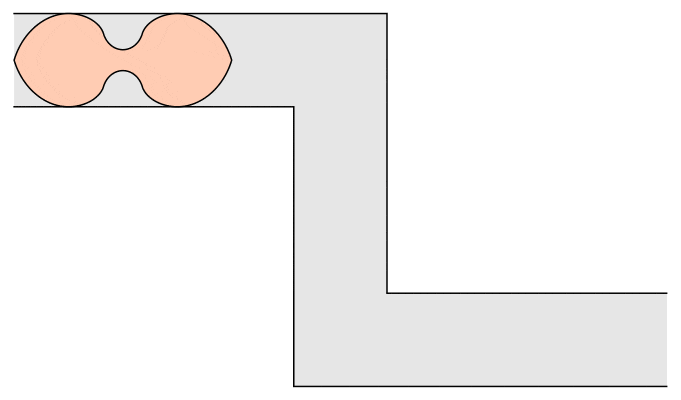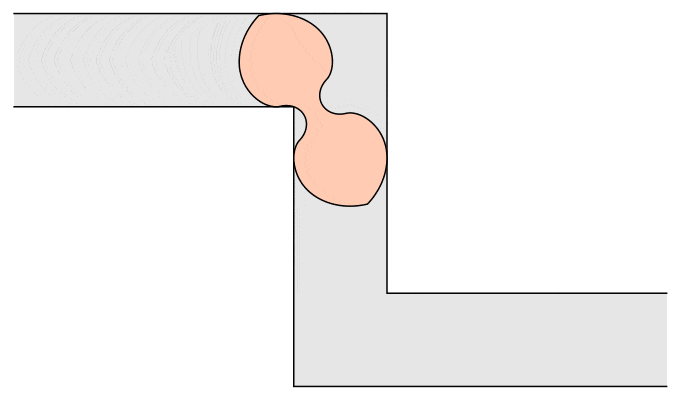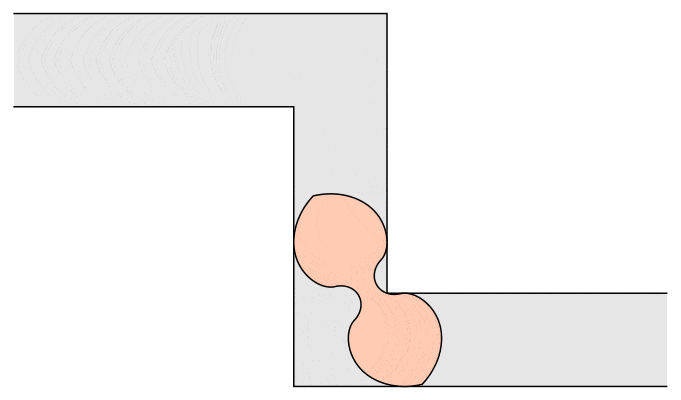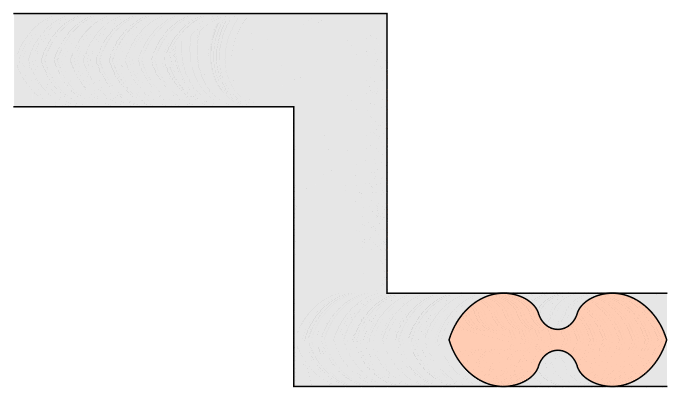
Of course, if a sofa can’t make it around one corner, it certainly can’t go around two, so the Kallus-Romik bound of 2.37 square units applies here as well.
It seems intuitively clear that the extra symmetry forced on you by the two corners will force you to use a skinnier sofa in this case. But Kallus-Romik left it as an open question to develop an ambidextrous version of their SofaBounds software. An enterprising computationally minded person should be able to get new and better bounds for the two-corner sofa moving problem.
Instead of trying to maximize the size of an object you are moving through a fixed-size region, you could instead ask about fixing the size of an object and minimize the size of the region around it. In 1917 Soichi Kakeya posed the Kakeya Needle Problem [4]:
If you have a needle of length one, what is the minimum area you need to be able to rotate it 360 degrees?
Obviously, you can do it using a circle of diameter one. Since this has area π/4 ≈ 0.79, the question becomes one of doing better. Anybody who has done a three-point turn to get their car turned around in a narrow roadway knows that with a little back-and-forth, you can get by with much less. For example:
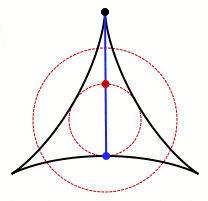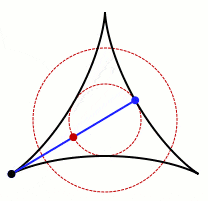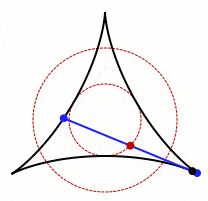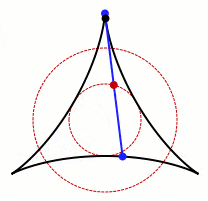
Amazingly, Besicovitch and others proved that you can find a region of arbitrarily small area which works! No matter how little area you allow, I can construct a region whose area is smaller and yet the needle can be rotated around while staying in the region!
This naturally leads one to wonder if it’s possible to rotate a needle around a region that has area zero. We know of regions (dots, lines, finite collections of dots and lines) which have area zero. It is awfully tempting to suppose that if we can rotate a needle using regions of arbitrarily small area, then there must be one with no area at all which still works.
Surprisingly, I learned from a blog post by Terry Tao that this impossible [5]. No matter how tiny, you need at least a smidge of area in order to rotate the needle. I also learned from Tao that the question of rotating a needle in three-dimensional and higher-dimensional spaces is still not entirely sorted out.
Lots of interesting questions to think about while we stay homebound.
Let’s think the unthinkable, let’s do the undoable. Let us prepare to grapple with the ineffable itself, and see if we may not eff it after all.
― Douglas Adams, Dirk Gently’s Holistic Detective Agency
[2] Image from Dan Romik’s webpage.
[3] If you’d like to read about their method, you can find their paper here.
[4] This is a mathematician’s needle: it has length, but no width. It is a separate, and probably harder, problem if you require me to also consider the width of the needle as a factor.
[5] See here.
