by Jonathan Kujawa
Four years ago was peak COVID-19. I was thinking about moving furniture, which led to this essay here at 3QD. The topic was the problem of moving a sofa down a hallway with a 90° corner:
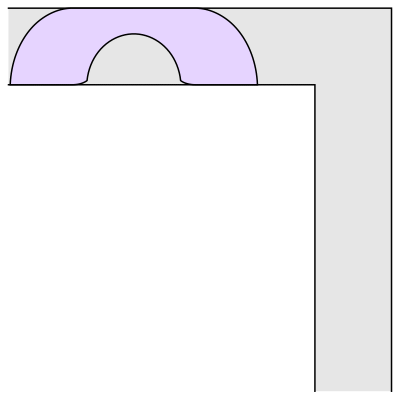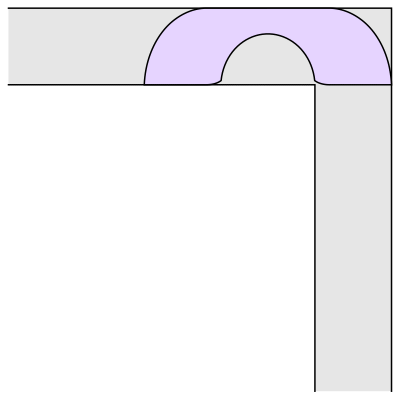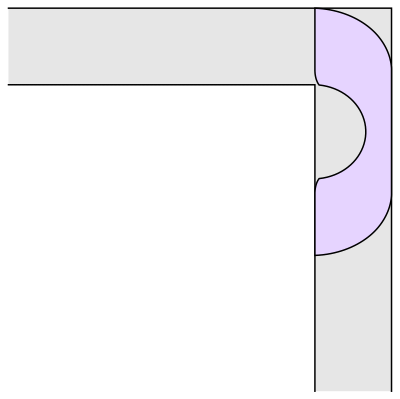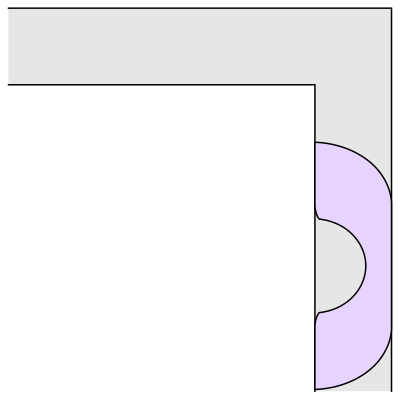
The problem is to find the “couch” of largest possible area that could be smoothly pushed down the hallway, around the corner, and then onwards. Leo Moser first asked this question in 1966 [1]. The image above is the couch found by Joseph Gerver in 1992. Gerver’s couch has an area of approximately 2.2195 square meters (where the hallway is exactly 1 meter wide).
As we talked about in that essay four years ago, Gerver used some clever math to find the shape of his couch. If you look very closely, you’ll notice that the corners are clipped off, and the inner semi-circle isn’t exactly a semi-circle. Without those tweaks, you have Hammersley’s couch from 1968, which has an area of π/2 + 2/π ≈ 2.2074 square meters. Several decades of time and Gerver’s hard work got us a whopping 0.0121 square meters.
 Of course there was no guarantee that Gerver’s couch was the biggest possible. Dr. Gerver’s approach made no promises that it gave the best possible, after all. A little more convincing is the fact that in 30 years we haven’t been able to do any better. But mathematics is a game of centuries and millennia — a few decades is small potatoes. In 2018, Yoav Kallus and Dan Romik proved that the couch could be no larger than 2.37 square meters. But the gap in size between Gerver’s couch and the Kallus-Romik upper bound is an order of magnitude larger than that between the couches of Gerver and Hammersley.
Of course there was no guarantee that Gerver’s couch was the biggest possible. Dr. Gerver’s approach made no promises that it gave the best possible, after all. A little more convincing is the fact that in 30 years we haven’t been able to do any better. But mathematics is a game of centuries and millennia — a few decades is small potatoes. In 2018, Yoav Kallus and Dan Romik proved that the couch could be no larger than 2.37 square meters. But the gap in size between Gerver’s couch and the Kallus-Romik upper bound is an order of magnitude larger than that between the couches of Gerver and Hammersley.
I’m not an expert in this area, but if you asked me a month ago, I would have said it could be many years before we’d resolve Moser’s couch question. Indeed, this could easily be out of reach forever. Many easy-to-state math questions are practically unsolvable. One could make infinitely many tweaks to Gerver’s couch as possible improvements. Or, you could do some entirely different shape, maybe something fractally and totally unexpected.
Part of the problem is that there is no single formula that gives you the area of all possible couches. If you had such a formula, you could try to maximize its output like you learned to do in your Calculus class. But if different shapes have different area formulas, there is no effective way to tackle them all at once.
This is no doubt my own human biases, but I find it a big bummer that Hammersley’s couch with an area given by a beautiful formula using pi is not the maximum. Once you show me that tweaks can give you bigger couches with ugly areas like Gerver’s, my hope for a definitive answer pretty quickly disappears.
So I was gobsmacked to see two interesting papers about Moser’s couch problem in the last few weeks.
The first is this paper by Kuangdai Leng, Jia Bi, Jaehoon Cha, Samuel Pinilla, Jeyan Thiyagalingam. In it, they use machine learning to investigate the couch problem.
There is a growing body of evidence that AI is a valuable tool in the search for examples and counterexamples. I recently saw a talk by Geordie Williamson at the joint meeting of the Australian, New Zealand, and US mathematical societies where he made exactly this point. Problems are often unsolvable because the full space of possibilities is massively too large to search by brute force. But, AI techniques can be used to do a more clever search that focuses on the places with the highest chance of success.
The paper by Leng-Bi-Cha-Pinilla-Thiyangalingam uses AI to attack both sides of the sofa problem. First, they use neural networks to search the universe of all possible couches that are able to travel down the hallway. The goal is to use the AI to find one with a large area. If Gerver’s couch is not the largest possible, then the AI might find a bigger one through its clever searching. As it turns out, the AI kept tending towards Gerver’s couch. This doesn’t mean a larger one is impossible, but it does give weight to the claim that Gerver’s couch is the largest possible.
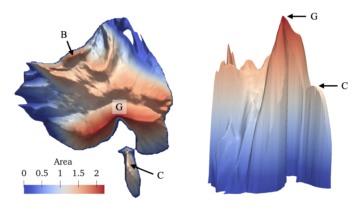
They also used neural network techniques to improve on the upper bound found by Kallus-Romik. In particular, they showed that these improved Kallus-Romik bounds appear to converge to the area of the Gerver couch:
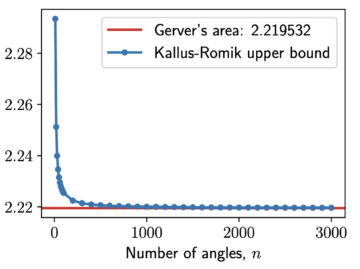
Both provide good evidence that Gerver’s couch is indeed the best possible. But evidence is not the same as a proof! In math, we want to know things with absolute certainty.
At the end of November, Jineon Baek, a mathematician from South Korea, dropped a bombshell on the ArXiv preprint server. They released a proof that the Gerver couch is indeed the best possible! Baek mentions that they used computer calculations in the early stages of working on this project, but the proof itself uses no computers, AI, or any of that high-tech stuff. It’s pure, uncut human mathematics. The general strategy is to show that a sofa that can move through the hallway must satisfy certain conditions and that Gerver’s sofa is the biggest sofa that satisfies those conditions and, hence, is the biggest possible. It is 120 pages of rather delicate computations.
It should be said that one should always be cautious with preprints. It is easy to make a mistake in 120 pages of math. Most are fixable, but some turn out to be fatal. I’m not an expert, and I can’t judge whether this paper will hold up. I will say that it passes the smell test of using the prior results and related mathematics in ways consistent with what I’d expect of a solution to the problem.
More importantly, Dan Romik is definitely an expert on the sofa problem, and Dr. Romik has confidently declared that Dr. Baek has solved the moving sofa problem. Presumably, he has read the paper in some detail and is confident it will stand up to scrutiny.
This is not the end of the story. John Conway asked about moving a sofa through a hallway with two 90° turns, and Dan Romik proposed the following peanut shape:
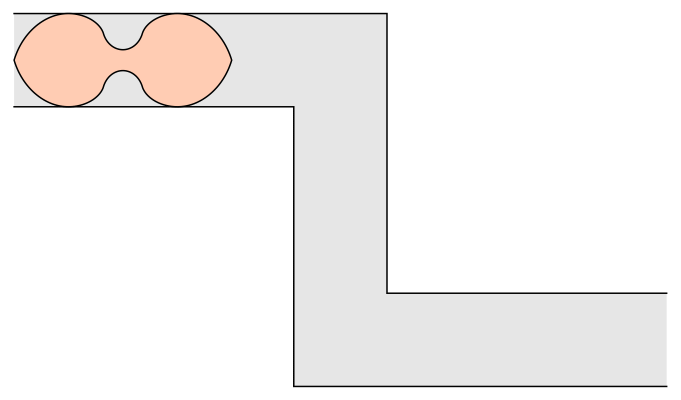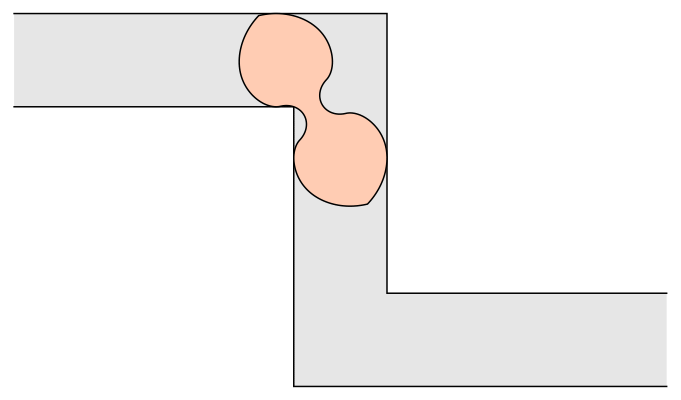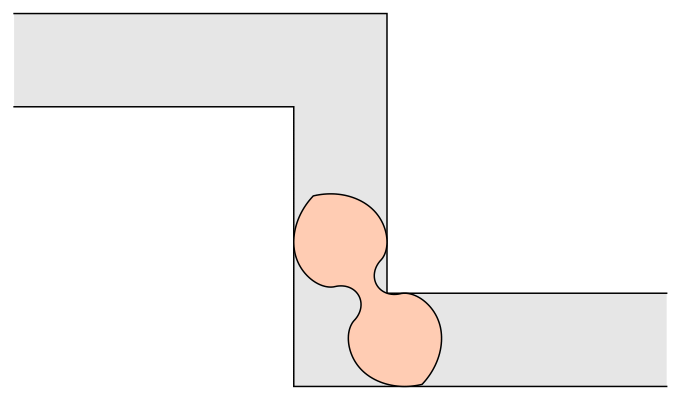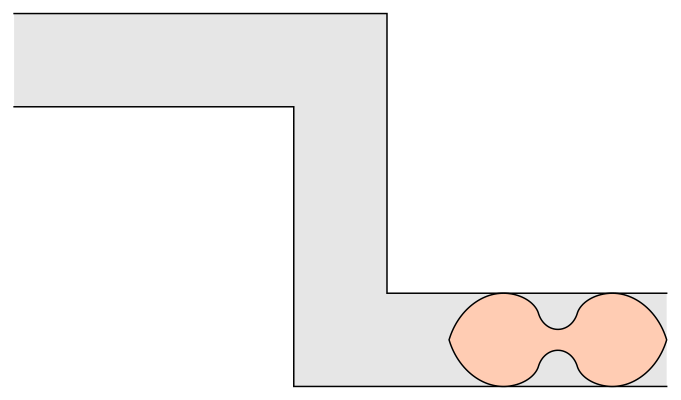
I would guess that Dr. Baek’s techniques should apply here as well, but that will need to be worked out.
A much harder problem is the 3D version of this problem. What if you wanted to move a 3D shape through an actual 3D hallway? Anyone who has moved furniture knows that you can do amazing things by twists, turns, and other clever maneuvers. Compared to the 2D problem, the universe of possible 3D couches and how they can move through a hallway is a vastly larger universe to search through.
As always, mo math, mo problems.
***
[1] Since couches go back to the Ancient Egyptians, if not further, I imagine some of the Pharoh’s servants asked the same question 3000 years before Dr. Moser.
***
Enjoying the content on 3QD? Help keep us going by donating now.
