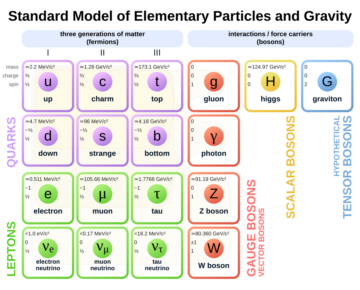
by Jochen Szangolies
In the previous two installments of this series ([1], [2]), I have been engaged in the project of communicating a bit of the intuition behind the abstract notions of physics (and the necessary mathematics). My guiding principle in this attempt (essay in the literal sense) has been a famous quote of Hungarian mathematician and polymath John von Neumann: “In mathematics you don’t understand things. You just get used to them.”
This is an initially surprising notion. Mathematics, it seems, is the domain of pure intellect, where great minds wrestle with arcane concepts to squeeze droplets of eternal truth from Platonic realms of pure form. How does this square with ‘just getting used to it’?
I think that the poles of this apparent dichotomy are not as far removed as it might seem. The traditional view seems to emphasize singular mental effort, while von Neumann intimates, rather, repeated exposure—training, or diligent practice. The first is the province of what Daniel Kahnemann calls ‘System 2’, the effortful, explicit, step-by-step mode of reasoning that is often implicitly meant simply by ‘thought’. We analyze novel concepts, break them down into their components, resolve them into a step-by-step, algorithmic sequence, much like taking apart a watch to find what makes it tick.
But practice targets a different, implicit and automatic mode of thought: that of ‘System 1’, the associative, fast and heuristic mode of cogitation at work when you perform activities that require little explicit thought. Take riding a bike: there is no hope to learn it purely via the System 2-mode—that is, you can’t read a book on bike-riding, hop on and be off on your merry way. You need, rather, to train—to try, fail, and try again, until you get it right; and once you do, you’ll find yourself at a loss explaining exactly how. But after you have learned to do it, it ceases to become an explicit effort, instead happening apparently ‘by itself’, without you having to attend to the precise sequence of motions that keep your feet cranking the pedals, your arms turning the handles, and your entire body holding the balance.
Practice imparts an understanding that can’t be achieved by direct instruction. Getting used to something is a way to understand it that bypasses and complements the step-by-step process of analytical reason, a way to appreciate it at an intuitive Gestalt level rather than from the bottom up in terms of its individual components.
This is of course well appreciated by working physicists and mathematicians. But both popular science writing and popular culture at large paint a radically different picture. Read more »