by Jochen Szangolies
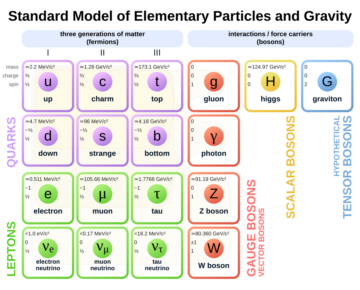
Modern physics in its full mathematical splendor introduces an array of unfamiliar concepts that daunt the initiate, and often even bewilder the pro (or is that just me?). A part of it is just that it’s a complex topic, and its objects of study are far removed from everyday experience: a quark or a black hole or a glueball is not something you’re likely to find on your desk. Well, maybe the latter, if you’ve been sloppy while crafting recently, but as so very often, physicists further confuse things by giving familiar names to unfamiliar concepts (spin, I’m looking your way).
But saying ‘it’s complicated’ is merely a fig leaf. Lots of things are complicated, and we manage to navigate them with ease. Many jobs involve reams of specialist knowledge, from plumbing to hedge-fond management, and even just navigating our webs of social relationships comes with considerable overhead. So what is it that makes physics special?
There is, of course, the already mentioned issue of the remoteness of its central concepts. Many of the complicated tasks we solve are so ingrained to us that we scarcely notice their complexity—the act of throwing a ball, or catching it out of thin air in flight, involves calculations that, in a realistic setting, stymied the efforts of robotics engineers for a long time. Likewise, the acquisition of language—even present-day Large Language Models (LLMs) still need to ‘read’ tens of trillions of words to acquire a degree of language fluency a human child can pick up just from what is spoken around them in their first couple of years. By comparison, an average reader would take something like 80.000 years of continuous reading time to ingest the text on which an LLM is trained!
These are tasks that, in some manner, are performed ‘natively’ by the human brain, without us noticing their complexity. Such tasks are sometimes classed as ‘System 1’-tasks in the dual-system psychology popularized by Daniel Kahnemann in his bestselling popular science book Thinking, Fast and Slow. In contrast, solving a mathematical equation or reasoning through a logic puzzle are step-by-step, explicit ‘System 2’-tasks you have to concentrate on—they’re not performed ‘by themselves’ the way catching a ball is.

But System 2-tasks can ‘migrate’ to System 1: think about how you used to have to reason through tying your shoelaces (‘the bunny runs around the tree…’), but now, it is an automatic task you don’t have to pay attention to. The reason for this is simple training: repeat something often enough, and it becomes part of your internal repertoire. (Indeed, this may be very much akin to ‘training’ in the neural network sense, an analogy I’ve explored previously.) This training is also what allows the plumber to navigate the complexities of their job with (greater) ease, and, crucially, what allows the physicist (or mathematician) to grapple with the abstract objects they encounter—as the polymath John von Neumann, widely held to be one of the greatest scientists and mathematicians of the 20th century, once remarked: “In mathematics you don’t understand things. You just get used to them.”
Thus, for some fluency in the abstracta of mathematics and physics, repeated exposure is key. If you meet something again and again, in different contexts, and apply it in different ways, you eventually get a handle at it—like tying your shoelaces, it becomes part of your repertoire.
But here, we reach a kind of impasse—there’s lots and lots of training you need to become a true expert at any given subject, which is infeasible for an interested observer to engage in. This leads to two problems: first of all, there are lots of people interested in physics—in what it has to say about our world, the discoveries made, the puzzles encountered. But the training these interested outsiders have access to is, by and large, really bad. Traditionally, it tends to fall into one of two groups—nontechnical and inaccurate, or accurate and impenetrable. The first one is the category of popular science books with unhelpful metaphors, such as rubber-mat spacetimes or famous physicists navigating conference crowds. The second are the dense missives of the physicists themselves, communicating ideas among one another, rife with jargon and symbols, and short on intuition and explanation.
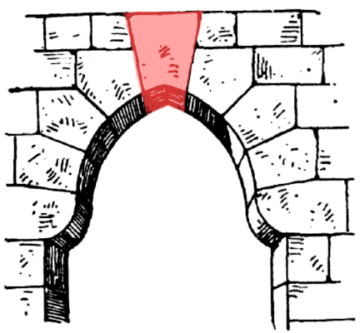
Within the second group, Ben Orlin from Math with Bad Drawings has recently put his finger on one particular issue with technical writing: it preserves only the ‘hard edges’ of thought, without presenting the actual work done to arrive at the final, pristine construction. A mathematical theorem as presented in the literature is something like a keystone arch: without any hint at the scaffolding used to erect it, its construction seems a mystery. How did the builders keep the stones from toppling over to insert the keystone giving it stability?
Compare this to the situation with plumbing. Most people simply aren’t that interested: your pipes leak, you call a pro to fix them. What arcane methods are used to do so simply aren’t a matter of concern. On the other hand, some do have an interest in enabling themselves to perform such fixes: these have a huge repertoire in DIY-books, YouTube-videos, ‘ELI5’-explainers and the like, focused on how to, you know, actually do stuff. These materials bridge the middle ground between high-level metaphor and professional, technical writing, and enable the DIYer to get started without having to immerse themselves in the full pro-level literature.
It is this middle ground where we find a mismatch between supply and demand in the literature on physics (and mathematics). However, in recent years, this situation has seen some improvement: perhaps starting with The Road to Reality by Nobel laureate Roger Penrose, a series of books has sought to explain the concepts of physics to the interested layperson without resorting to too many white lies. This has resulted in a corpus of works that can be used to bridge the gap: starting with fairly illustration-heavy works such as the aforementioned one by Penrose, eventually leading up to texts that don’t shy away from graduate-level mathematics, but presents it in a way that’s rich in example and intuition, like Anthony Zee’s Quantum Field Theory, as Simply as Possible.
While this is undoubtedly a welcome development, it doesn’t seem to have had much impact on short form science writing, so far. There, we still find mostly a division between classic ‘pop-sci’ level articles, and the terse, technical missives we physicists use to communicate among ourselves. One reason for this is that there is not much reward to writing such texts: the physicist typically has their plate full with writing the technical articles, not to mention grant proposals and project outlines, on top of actually doing the work they’re communicating; while most science journalists can’t be simultaneously expert enough in all the fields they need to cover to produce in-depth, but still approachable writing.
So we’re faced with a mismatch: a public with great interest in a topic in need of the ‘training data’ to build the internal models to navigate its complexities, and a lack of incentive to produce this data, in the form of sharing the intuitions that guide the technical work—the scaffolding to hold up the two halves of the arc before the keystone is placed.
With this (somewhat lengthy) preamble in mind, I want to share some of the background ideas behind a concept that’s become important to some of my recent ideas, which also gives me an opportunity to talk about a notion that’s hugely important in modern physics, but which has scarcely found its way into popular writing—the idea of a fibre bundle, and more concretely, the so-called Hopf fibration.
Decorating Space
Physics is, broadly speaking, the study of stuff moving through space (and time). (And sometimes, also how space and time reacts to stuff moving within it, but we’ll ignore that for the moment.) So if we think of space as the arena of where things happen, we need a way to represent what’s going on at each point of space. A structureless point particle will just trace out some curve through space: we can describe it just by the set of points it occupies at successive instances of time. But physically interesting objects generally have more structure than that: they have a certain spin, or a particular charge, for instance. Thus, we need a way to keep track of these additional data; but space alone gives us only the position. We need some way to augment our description.
That augmentation comes in the form of a fibre bundle. To build some intuition, think of space as an empty field, and then sow some wheat: at each point, a wheat stalk grows. Viewed from far away, this turns the initially two-dimensional plot of land into a three-dimensional block, whose thickness is given by the wheat ‘fibres’. The two-dimensional ‘base’ is still used to give the position of a particle, but now, we have an extra degree of freedom along the length of the stalk—the fibre—to use for our description.

Now, this sort of bundle is still too simple for our purposes. One reason is that it’s a so-called trivial bundle: the fibre is attached to the base everywhere in the same way. If you know one ‘patch’ of the field, you know all there is to know. But in physics, there are often also global notions that aren’t obvious from such a local perspective. Roughly speaking, this is needed to account for the fact that if you change the parameters of a system in such a way that at the end, they return to their original values (you take a ‘loop’ through some abstract parameter space), not everything is equal: there might be a ‘memory’ of this trip in the change of some quantity.
An example of this can be given as follows: extend your arm forwards, palm open, thumb pointing up, as if you were very stiffly aiming to shake hands with someone. Then rotate the arm by ninety degrees up, so that your extended fingers point straight at the ceiling. Now rotate it to the side, so that it lies on the axis of your shoulders; your thumb now points backwards. Then bring it back to the front: your arm now points in the same direction as before, but your thumb has been rotated by ninety degrees. Another everyday example is the way a cat manages to right itself in falling: if its feet point up at the start, and it has zero angular momentum, it will perform a series of internal twists that leads it through a rotation of 180°, even though it has no angular momentum at any point throughout the fall, since that’s a conserved quantity. (Please don’t drop any cats by way of experimental confirmation. They’re abused enough in physics as is.)
We can model this behavior in the following way. Take a not-too-wide strip of paper, and mark a point at some random place (but not exactly in the center of its height). Then draw a line through the point so that it stays at a constant ‘height’.

Then, glue the edges of the strip together, so that it forms a cylinder. We can interpret this cylinder as a fibration: the base space, a circle, has a line segment attached to every point.

We can view this as transporting a point around the base circle, while keeping its image in the fiber at constant height. Once we come back to the original point, nothing has changed: its image returns to the same point. (Think of wheat stalks planted in a circle.)
But now cut the strip apart vertically through the marked point, give one of the ends a twist of 180°, and glue them back together. The resulting shape is the famous Möbius strip, a non-orientable surface, meaning that it has no front- and back-side (you can trace along the entire surface without lifting your finger).

Now, the point will no longer return to its original spot: the prescription of ‘walking along the circle at a constant height of the fiber’ suddenly ends up at a different place, because the fiber itself twists around the base space. (In mathematical terms, just so you’ve heard the jargon, this illustrates the anholonomy of the Möbius strip.) This is just as with the cat: after taking a journey through ‘shape space’, returning back to its original shape, it has acquired an overall rotation.
Thus, it is only by introducing this twist that we can capture phenomena where the global structure of the total space introduces relevant changes. Note, though, that locally, the Möbius strip is still a circle with line segments ‘glued’ to each point—which illustrates that the phenomenon is a truly global one and not visible on the purely local level. This is what makes the Möbius strip a simple example of a nontrivial fiber bundle, in which the ‘local’ structure of a point and its attached fiber doesn’t suffice to tell the whole story.
Wheels Within Wheels
In physics, fiber bundles come into their own in the description of elementary particles and the forces between them by means of so-called gauge theories. I will not go further into detail here, except as to note that, implicitly, we have already made acquaintance with this notion: in my discussion of how electric forces emerge from interference effects, the phase degree of freedom attached to an electron can be viewed as a fiber consisting of a circle attached to the base space giving its path. Then, the fact that one can sometimes move an electron along a loop back to its origin and acquire a difference in phase (a so-called Berry phase) is testament to the nontriviality of the entire bundle.

One bundle of particular interest is the so-called Hopf fibration, after German mathematician Heinz Hopf, who discovered it in 1931. Its fiber, as in the description of the electron above, is just the circle, S1 in mathematics. Its base space is the sphere in three dimensions, S2—that is, the two-dimensional surface of a ball in three dimensions. Thus, an entire S1 is attached to every point of S2, but again, in a nontrivial way—the fibers twist around one another. Moreover, the entire space—base and fiber—yield the four-dimensional sphere, S3, i.e. the set of all points in four dimensions a constant distance (the radius) from the origin. Thus, we can decompose the four-dimensional sphere into a base consisting of the three-dimensional sphere with a circle as fiber in a nontrivial way, just as we can decompose the Möbius band in terms of a circle as the base space, and a line segment as fiber.
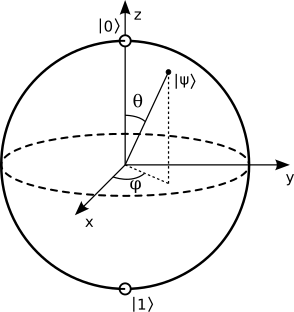
The Hopf fibration was one of the first examples of a nontrivial fiber bundle. It turns out to have interesting connections to physics: for one, it gives the state space of a single qubit, the most simple quantum mechanical system. But what I find more intriguing is that there are just two straightforward generalizations of this construction: the description of the eight-dimensional sphere S7 as an S3-bundle over an S4-base, and the description of the 16-dimensional sphere S15 as an S7-bundle over an S8-base. Beyond these, no further spheres are describable in terms of such a fibration.
Moreover, each of these can also be interpreted in terms of quantum mechanics: as a system of two and three qubits, respectively. This might seem surprising, at first—two parameters are enough to describe a single qubit as a point on S2, so what do the extra coordinates needed to parametrize S15 amount to? As it turns out, these keep track of the entanglement between the qubits in a systematic manner. Additionally, as a final teaser, once we ‘fix’ which coordinates describe the qubits, and which describe the entanglement, that ‘fixing’ has a natural symmetry given by the group SU(3) × SU(2) × U(1)—the same symmetry defining the forces of the Standard Model of elementary particles (in essentially the same manner as we have previously seen the group U(1) alone—that is, the group of rotations through a circle—give rise to the electromagnetic force).
Is that a coincidence, or something that, like the matching shape of the continental outlines of Africa and South America, hints at some deeper connection? I have argued that it might well be the latter. But digging into this somewhat further will have to wait for another time.
