by Jochen Szangolies
In the previous two installments of this series ([1], [2]), I have been engaged in the project of communicating a bit of the intuition behind the abstract notions of physics (and the necessary mathematics). My guiding principle in this attempt (essay in the literal sense) has been a famous quote of Hungarian mathematician and polymath John von Neumann: “In mathematics you don’t understand things. You just get used to them.”
This is an initially surprising notion. Mathematics, it seems, is the domain of pure intellect, where great minds wrestle with arcane concepts to squeeze droplets of eternal truth from Platonic realms of pure form. How does this square with ‘just getting used to it’?
I think that the poles of this apparent dichotomy are not as far removed as it might seem. The traditional view seems to emphasize singular mental effort, while von Neumann intimates, rather, repeated exposure—training, or diligent practice. The first is the province of what Daniel Kahnemann calls ‘System 2’, the effortful, explicit, step-by-step mode of reasoning that is often implicitly meant simply by ‘thought’. We analyze novel concepts, break them down into their components, resolve them into a step-by-step, algorithmic sequence, much like taking apart a watch to find what makes it tick.
But practice targets a different, implicit and automatic mode of thought: that of ‘System 1’, the associative, fast and heuristic mode of cogitation at work when you perform activities that require little explicit thought. Take riding a bike: there is no hope to learn it purely via the System 2-mode—that is, you can’t read a book on bike-riding, hop on and be off on your merry way. You need, rather, to train—to try, fail, and try again, until you get it right; and once you do, you’ll find yourself at a loss explaining exactly how. But after you have learned to do it, it ceases to become an explicit effort, instead happening apparently ‘by itself’, without you having to attend to the precise sequence of motions that keep your feet cranking the pedals, your arms turning the handles, and your entire body holding the balance.
Practice imparts an understanding that can’t be achieved by direct instruction. Getting used to something is a way to understand it that bypasses and complements the step-by-step process of analytical reason, a way to appreciate it at an intuitive Gestalt level rather than from the bottom up in terms of its individual components.
This is of course well appreciated by working physicists and mathematicians. But both popular science writing and popular culture at large paint a radically different picture. Take this exchange from Marvel’s The Avengers:
Maria Hill: When did you become an expert in thermonuclear astrophysics?
Tony Stark: Last night. The packet. Selvig’s notes, the extraction theory papers. Am I the only one who did the reading?
The intimation here is that Stark, due to his brilliance, needed only to ‘do the reading’ in order to acquire an expert-level grasp. And that’s by and large the popular perception of understanding something: if you’re smart enough, all you need is to ‘do the reading’. But that’s just not right. You need to do the doing as well.
This mistaken perception is exacerbated both by most popular science writing, which substitutes misleading metaphor in place of in-depth Gestalt understanding, and by the dense, symbol-ridden papers and books scientists write to communicate among themselves, which preserve only the ‘hard edges’ of thought while hiding the scaffolding used to erect these austere theoretical structures. Of course, this seems to make proper science communication prohibitively difficult: non-experts really can’t feasibly ‘do the doing’ necessary. There just aren’t enough hours in the day. But is there a middle way?
I think there is: rather than exhibiting only the finished product, the hard-edged architectures of intricate theory, communicate something of the scaffolding itself. That is, try and formulate the intuitions behind the research, the gut feelings, false starts and blind avenues, the promising leads that ended up extraneous diversions, and so on. Give an account of the journey, rather than just the destination. At least some part of what training and repeat exposure builds up in the practitioner is a set of robust heuristics that may be used to investigate promising leads and ideas, forge footpaths later to be reinforced with rigor.
The simplest chess algorithms compute all possible moves explicitly to a certain depth, then select the ‘best’ one. This is the ‘doing the reading’-way of understanding: knowing nothing but the rules of chess, in principle, a sufficient intellect could calculate the best move in every situation. Human minds don’t work like that. Rather, having played sufficiently many matches, the game is appreciated at the level of tactics and strategy—relieve pressure on the flank, open routes into the opponent’s ranks, and so on. All of these can eventually be turned into explicit series of moves, but that may not be the best way to communicate them. Rather, it may be better to focus on the intuitions themselves, to give a justification of a given move without having to go all the way down through the tree of possibilities. Such heuristics form an ‘intermediate’ level between the explicit, but indigestible System 2-description and a System 1-appreciation that needs long hours of practice.
Hence, my essay of transmitting some of the guiding metaphors of my own research on here.
A Hopf, A Skip, And A (Quantum) Jump
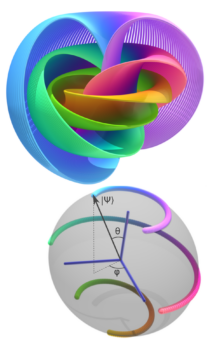
The first column in this series introduced the notion of the Hopf fibration, a particular way to view a sphere in four dimensions in terms of the ordinary sphere in three dimensions with a circle ‘pasted onto’ every point on the surface. A fibration, in general, is a way to add ‘extra data’ to a space—in fundamental physics, fibre bundles are, for instance, used to model particles that have ‘internal’ properties beyond just their position in space. A field of wheat, or a hair brush, is an often-used example of such a bundle: a ‘stalk’ placed at every point of the ‘base’ space.
Such fibre bundles aren’t very interesting, however—the fibre is attached to the base in the same way each time, so if you know the space at one point, you know all there is to know. More interesting (‘nontrivial’) fibre bundles are obtained when you let the fibres ‘twist around’ in a way such that the global properties are no longer obvious from just the local structure.

An example of such an interesting bundle is the Möbius-strip, which can be created by gluing a strip of paper top to bottom. If you now take a point at a fixed ‘height’ above the base (say, the lower edge of the original strip), and take it once around, it won’t end up in the same place again: even though you take a prescription that’s the same at every individual point, you eventually accrue a stark difference to the original setting. The same thing can be illustrated by transporting an arrow along arcs of a sphere, keeping the orientation at every point fixed: when you reach the origin again, the arrow will have accumulated a rotation. The lesson of this is: local data don’t always fix global phenomena!
In the second column, we then took a look at how the Hopf fibration can be used to represent the state of the most elementary quantum system, the qubit. A qubit is characterized by always assuming one of two possible states upon measurement, thus making it the quantum analogue of the classical bit; and like the classical bit, it can be seen as an abstraction of different physical systems—photon polarizations, electron spins, electric currents in superconducting junctions, and so on. Our main lesson there was how the geometry of this space introduces the possibility of quantum interference: the sphere in three dimensions (of radius 1) is defined by x2 + y2 + z2 = 1, but since squares of negative numbers (or even complex ones) are always positive, that means that various components can ‘cancel out’, with thus individually allowed options becoming forbidden when taken together.
However, in the Hopf fibration, this sphere only yields the base space. What about the fibre? To any point on the surface of the sphere, a circle is attached, in such a way that these circles ‘twist’ around one another—indeed, any two circles are connected, forming a so-called Hopf link. This ‘circle’, in quantum mechanics, is the phase of the system, and it is what determines interference phenomena: a relative difference in phase reinforces or cancels out the probability of a particular option obtaining. In the discussion of the previous column, we saw this in how the component of the system taking the ‘lower’ path through an interference experiment acquires a relative minus sign (a phase rotation of 180°), leading to destructive interference. More pictorially, we can think of the phase as a little ‘clock hand’ rotating along with the movement of a system.
Twice The Fun
Looking at single qubits on their own misses one of the most surprising phenomena of the quantum world: quantum entanglement. Even though, in general, the quantum formalism does not assign definite values to all possible quantities, instead only producing probability assignments, it may make definite predictions regarding the correlation of such quantities: for instance, it may be up to (equal) chance whether you find the value ‘0’ or ‘1’ for your qubit, but then, the value of a distant qubit may be absolutely fixed to be opposite yours. Moreover, you might measure your qubit in different ways—say, measure a spin along different directions—while still finding the distant qubit perfectly anticorrelated.
However, when we straightforwardly extend our above description to two qubits, no such phenomena seem apparent. What we seem to get is simply two copies of the Bloch sphere, with each describing a quantum state entirely independently of one another. But this is too naive.
Two qubits can be found in the possible states [0,0], [0,1], [1,0] and [1,1]. Recall the convention that the brackets ‘[.]’ simply signal a quantum object, with whatever noted in between just providing a ‘name’ or ‘label’ for a particular state—so we have simply chosen to label each possible state by the values we find for each qubit. But according to the laws of quantum mechanics, a general state is then any particular sum of all of these possibilities, e.g.
a∙[0,0] + b∙[0,1] + c∙[1,0] + d∙[1,1].
Each of the factors a–d now gives, when squared, the probability of finding the respective configurations; thus, their squares must sum to one (something must always happen). Recalling now that each of these coefficients is a complex number, and hence, equal to two real numbers, we have a set of eight numbers whose squares sum to one. This is the defining equation for a single, seven-dimensional sphere, rather than two two-dimensional ones. (That is, two copies of the ordinary sphere in three dimensions; recall that a sphere in n dimensions is an n – 1 dimensional object, e.g. the sphere in two dimensions, the circle, is a one-dimensional curve.)
What does this mean? Again, we can use the notion of a fibre bundle to shed some light on the issue. Just like the three-dimensional sphere (the sphere in four dimensional space) can be considered as a two-dimensional sphere with a circle fiber, the seven-dimensional sphere can be considered as a four-dimensional sphere, each point of which has a three-dimensional sphere attached: this is the second Hopf fibration. Just as the circles twist around each other in the first one, so do the three-spheres here—although visualization is somewhat more challenging.
Now, what does this have to do with entanglement? Well, recall that a single qubit state is given by a three-dimensional sphere. So, we can, in fact, consider the fibre of the second Hopf fibration to give the state of one of the two qubits. That state then changes based on the point of the base space where it is attached—the non-triviality of the fibre bundle ensures that we can’t associate a single, global state to each point of the base space. Thus, different points of the base space are associated with different states for one of the qubits—a phenomenon already reminiscent of the notion of entanglement.
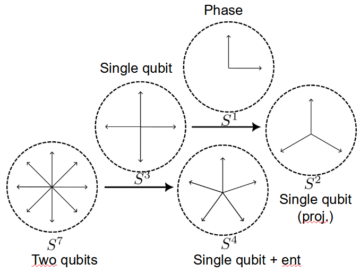
But what does the point in the base space represent? A natural guess would be the state of the other qubit: then, that state would dictate the state of the qubit in the fibre, as their entanglement would have us expect. But the base space is a four-dimensional sphere, thus each point is given by five parameters (again, consider how each point on the circle is given by an x– and a y-coordinate). But a full description of a single qubit state only needs three parameters!
The puzzle is resolved by noting that any given non-entangled state actually lives in a two-dimensional sphere within the base space (just as how a point with z = 0 lives in a circle in the x-y plane). Moreover, the entire construction in this case just yields two copies of the Bloch sphere—that is, two independent sets of parameters. Thus, the base space of the second Hopf fibration keeps track both of the state of the second qubit, and of how it is entangled to the first—and fixing that then yields the state of the first qubit, too.
The reason this is necessary is that qubits can be entangled in different ways—not only can their values upon measurements be opposite or equal, entanglement also comes in different strengths. Indeed, the two ‘extra’ coordinates quantify the strength of the entanglement between the two qubits!
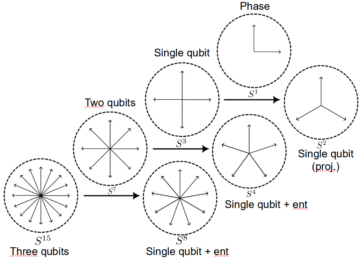
Where the first Hopf fibration gave us insight into the notion of quantum interference, the second Hopf fibration allows us to keep track of the way two qubits may be entangled. Does the story end here? Well, not quite: there is a third Hopf fibration, which can be used to describe the entanglement of three qubits. We find much the same picture: the base space contains the state of one single qubit, plus additional parameters quantifying the entanglement with the other two qubits, which live in the fibre.
Much more could be said about this intriguing construction. However, my aim here was neither to give a detailed account, nor to be content with shallow metaphor: rather, I want to present a slice of how I tend to think about these notions, in the hope that communicating this sort of working heuristic helps lay the tracks for the sort of understanding only available via repeat exposure. Thus, don’t fret if not everything is completely clear on a first read-through. But perhaps, a little bit of intuition might stick with you—with your own System 1-heuristics. And maybe, a little more might stick next time. And then eventually, things might actually start to make sense.
