by Ashutosh Jogalekar
Physicists writing books for the public have faced a longstanding challenge. Either they can write purely popular accounts that explain physics through metaphors and pop culture analogies but then risk oversimplifying key concepts, or they can get into a great deal of technical detail and risk making the book opaque to most readers without specialized training. All scientists face this challenge, but for physicists it’s particularly acute because of the mathematical nature of their field. Especially if you want to explain the two towering achievements of physics, quantum mechanics and general relativity, you can’t really get away from the math. It seems that physicists are stuck between a rock and a hard place: include math and, as the popular belief goes, every equation risks cutting their readership by half or, exclude math and deprive readers of a deeper understanding. The big question for a physicist who wants to communicate the great ideas of physics to a lay audience without entirely skipping the technical detail thus is, is there a middle ground?
Over the last decade or so there have been a few books that have in fact tried to tread this middle ground. Perhaps the most ambitious was Roger Penrose’s “The Road to Reality” which tried to encompass, in more than 800 pages, almost everything about mathematics and physics. Then there’s the “Theoretical Minimum” series by Leonard Susskind and his colleagues which, in three volumes (and an upcoming fourth one on general relativity) tries to lay down the key principles of all of physics. But both Penrose and Susskind’s volumes, as rewarding as they are, require a substantial time commitment on the part of the reader, and both at one point become comprehensible only to specialists.
If you are trying to find a short treatment of the key ideas of physics that is genuinely accessible to pretty much anyone with a high school math background, you would be hard-pressed to do better than Sean Carroll’s upcoming “The Biggest Ideas in the Universe”. Since I have known him a bit on social media for a while, I will refer to Sean by his first name. “The Biggest Ideas in the Universe” is based on a series of lectures that Sean gave during the pandemic. The current volume is the first in a set of three and deals with “space, time and motion”. In short, it aims to present all the math and physics you need to know for understanding Einstein’s special and general theories of relativity.
Needless to say, this is a very ambitious goal. Special relativity needs relatively simple math – it’s the physical picture that’s mind-bending and challenging to comprehend. But general relativity needs an understanding of differential geometry and tensor calculus, two subjects which, unless you are a graduate student in physics (and even then not always) you are unlikely to encounter. Even Einstein needed a couple of years to bring himself up to speed on this math. Sean’s book won’t fully substitute for a deep understanding of differential geometry and tensor calculus, but it will certainly help you gain an appreciation of these areas that surpasses a purely popular account like Brian Greene’s “The Elegant Universe” or Stephen Hawking’s “A Brief History of Time”. In short, if you have a high school background and get to the end of this book with diligence, Einstein’s field equation relating the geometry of spacetime curvature to the distribution of matter in spacetime will no longer look like Latin and (literally) Greek to you.
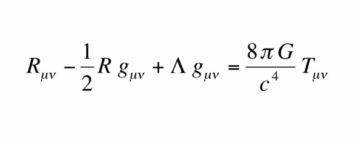
Sean’s two big strengths are an easy, informal manner of exposition and a gift for focusing on the physics and not letting the reader get lost in the weeds. The book has nine chapters: Conservation, Change, Dynamics, Space, Time, Spacetime, Geometry, Gravity and Black Holes. There is an elegant logical progression in these chapters. The discussion starts with a general look at the philosophy of physics, at symmetry and conservation laws, at models (the “spherical cows” of physics) and theories. It makes the cogent point that for all its perceived difficulty, physics is often simpler than biology or chemistry because you can actually strip away many of the complications of reality and still get a working model to which you can then gradually add those complications.
The next few chapters deal with the basic mathematical apparatus needed to understand physics: calculus. I mentioned before that the book assumes only a knowledge of high school math, but I will say that if you have already studied derivatives and integrals in college or graduate school, this material will come to you more intuitively. After a discussion of the basics of calculus as a tool to understand change, the book moves on to exploring some of the basic ideas of classical physics, including force, velocity, momentum and acceleration (relativity is a classical theory, so one can get away with studying quantum mechanics). Some of the simpler systems of classical mechanics including oscillators are discussed. In the world of classical mechanics, all you need to know are the starting positions and velocities of particles composing a system, and then you can predict the state of the system at any future point. This vision of classical mechanics was the vision of a deterministic cosmos, one that was shattered by the discovery of quantum mechanics.
One of the strengths of the book is that it introduces both Lagrangian and Hamiltonian mechanics at a comprehensible level. Lagrangian mechanics manifests itself in the principle of least action, which Richard Feynman once called a turning point in his career as a physicist. There is a quantity called the action in physics, which is the difference of the kinetic and the potential energy (defined as the Lagrangian) integrated over time. It turns out that nature often behaves in such a way that this action is minimized. In optics the principle is known as Fermat’s principle of least time, and Feynman himself used it very effectively to formulate a new theory of quantum electrodynamics. When you read about it for the first time, the principle of least action seems a bit magical – how does nature know what the path of minimum action for a process is? – and Sean conveys this power and sense of wonder well. I’ve always thought that even freshman or sophomore students could be introduced to the power of Lagrangian mechanics through the principle of least action, and the discussion in the book would be a simple way to do it.
The same goes for Hamiltonian mechanics which the book discusses in the chapters titled ‘Dynamics’ and ‘Space’; this is also where partial derivatives need to be introduced. In Hamiltonian mechanics, the basic twin properties of position and velocity are replaced by position and momentum. A common question for those encountering Hamiltonian mechanics for the first time is: why replace velocity with momentum when one can easily get the momentum by multiplying the mass by the velocity? There is a subtle, non-obvious reason why it makes sense to regard the momentum and not the velocity as more fundamental. Sean explains it well (in a nutshell, momentum is more generalizable than velocities and Hamilton’s equations are more general than Newton’s and can be used in more complex situations), but I do think that this is one of those points which can only be appreciated in the context of more advanced topics like quantum theory and statistical mechanics. Nevertheless, I am glad the book explains it: along with Lagrangian mechanics, I do think that Hamiltonian mechanics can be explained at least in a rudimentary manner in simple language the way it’s done here.
The next few chapters are where the book really starts gathering steam, since the treatment of calculus and basic concepts of physics sets you up to start appreciating some of the subtleties of time. To understand what is called the ‘arrow of time’, you need to understand not just Newtonian mechanics but also thermodynamics. The book spends some time on exploring the key concept of entropy which is intimately entangled with past and future; for a fuller treatment I will recommend Sean’s own earlier book, “From Eternity to Here”. One of the wondrous things about Newton’s laws is how they are reversible at a microscopic level: if you try to reverse the breaking of a teacup as it falls to the floor, there is nothing in Newtonian mechanics that prevents it. It’s the macroscopic improbability of the process, related to entropy, that prevents it.
At this point, the book has set us up for the denouement: the chapters on spacetime, geometry and gravity. This part of the book is frankly a tour-de-force; I vividly remember reading it and finishing the book on a flight and appreciating how accessible and masterful the discussion was. Throughout the focus is on the physics, and Sean also dispels some commonly held myths about relativity during the process. Special relativity arises from just two postulates: first, that the laws of physics are the same in all inertial frames of motion (frames without acceleration) and second, that the speed of light is constant. The first principle was known since Galileo, but the second one was enshrined into physics by Einstein and was revolutionary: it led to an overthrow of the Newtonian concept of absolute time. Other physicists like Hendrik Lorentz and Henri Poincare came close to doing this, but neither had the unparalleled insight into physical pictures and fearlessness that Einstein exemplified. After Einstein came up with his theory in the miracle year of 1905, Hermann Minkowski postulated the existence of a four-dimensional spacetime, dissolving the previous boundaries between space and time that had been held since antiquity.
One of the more bizarre aspects of relativity that strikes readers right at the beginning is how the geometry of spacetime can be counterintuitive. For instance, the shortest distance between two points in ordinary space is a straight line, but it turns out that in spacetime, this straight line corresponds to the longest time. This explains the s0-called twin paradox (which, as Sean emphasizes, is only a paradox if you aren’t steeped in the new view of the world that relativity conjures up). A twin who goes somewhere far to a different galaxy may seem like she’s following a longer path in space, but she’s also following the shorter path with reference to time. Another common misconception that’s cleared up: clocks don’t actually tick slower in their reference frame for the far away twin. Along with the time dilation associated with the twin paradox and length contraction, this chapter also introduces the idea of the Minkowski metric which is a version of the Pythagorean theorem of spacetime, with a crucial difference: there’s a minus sign that gets applied to the time term, which accounts for the aforementioned phenomenon of longest distance corresponding to shortest time. The chapter on spacetime also contains a simple derivation of Einstein’s famous formula relating mass and energy.
The metric is, in fact, the central mathematical object in relativity. It allows us to define distances (characterized by “line elements”) in spacetime and thereby to determine the geometry of spacetime. Hints that he would somehow have to know more about the geometry of spacetime came to Einstein when he came up with his famous principle of equivalence which says that in small regions of spacetime, the effects of gravity are indistinguishable from the effects of acceleration. What is the best way to describe the effects of acceleration in the geometry of our universe? It is at this point that Einstein had a genuine breakthrough (as if he hadn’t had enough breakthroughs before). He realized that in order to extend relativity to accelerated frames and gravity, he would have to consider spacetime not as flat but as curved. With help from his friend Marcel Grosmann, Einstein was thus led to the study of differential or Riemannian geometry, which is essentially the study of geometry of curved surfaces. On curved surfaces, the usual axioms of Euclidean geometry, such as the well-known postulate that the sum of the three angles of a triangle is 180 degrees, do not hold.
The chapter on geometry in the book deals with a few concepts from Riemannian geometry, although a fuller understanding would need greater study of specialized books (see Needham below). Nonetheless, the basic ideas are not impossible to understand. Differential geometry has an august history. It originated with efforts by the great mathematician Carl Friedrich Gauss to describe the intrinsic curvature of surfaces. A key concept is the manifold: as Sean explains, just like the effects of gravity are indistinguishable from acceleration in small regions of spacetime, the effects of curvature can be neglected and the principles of Euclidean geometry applied in small spaces. A manifold is a curved surface which is nonetheless ‘locally Euclidean’. It enables a way for us to ‘do geometry’ on curved surfaces. A particularly marvelous notion here which the book explains clearly is that of parallel transport, which is a way of moving vectors and distances around a curved surface on a manifold. The concept of a parallel manifold leads to the Riemann curvature tensor which is again a mathematical tool for describing the curvature of surfaces at every point. Tensors are discussed rather briefly in the book, but they were the other big mathematical innovation that Einstein needed along with differential geometry, especially in describing the matter distribution in a region of space (the so-called energy-momentum tensor).
The discussion of curvature, surfaces and the Riemannian curvature tensor sets the book up for discussing the crown jewels of relativity, the Einstein field equations. Here’s where Sean does a good job teaching the reader how physicists think. Enrico Fermi was famous for first working out the physical picture, setting down the relevant parameters and thinking about their proportionalities before plunging into solving the equations. Einstein was similar. He now had all the tools at his disposal: the metric tensor that describes the geometry of spacetime, and the energy-momentum tensor that describes the matter distribution. More specifically, he needed what is called the Ricci tensor instead of the Riemann curvature tensor. Once he had all these tools in hand, Einstein “merely” had to find the right equation relating the geometry on one side of the equation (the R and the g in the equation above) to the matter distribution on the other side (the T above), all while respecting the basic postulates of relativity. Sean shows how basic considerations of symmetry and mathematics (especially related to the indices in which these objects are expressed) allowed Einstein to finally find his famed field equations.
In the last chapter, the book discusses the application of general relativity to practical problems, including the precession of Mercury’s orbit (when Einstein could calculate the correct value, he reported feeling that “something had snapped” inside him), the expansion of the universe and black holes. We are shown how Karl Schwarzschild calculated the metric for a spherically symmetric body in a vacuum and how this describes black holes and the singularities in them. The book ends with a discussion of some of the key properties of black holes like the area theorem. Black holes were the biggest and most fascinating prediction of Einstein’s theory, and yet he never believed in them.
“The Biggest Ideas in the Universe” is a great introduction to relativity for those who always wanted to learn physics but who don’t want to completely skip the math and are willing to spend some time thinking about what equations mean. And although not a textbook, I could see it being excellent additional reading material for high school graduates who are entering college and who might be aching to learn something about the most exciting parts of physics without having to spend three or four years going into the details of inclined planes and electromagnetic theory; in fact I think it would prime the mental pump for these students and inspire them to study these topics further. In general the book succeeds remarkably well, although you may want to supplement some of the hairier ideas about the mathematics of general relativity with other reading (I provide a short personal list of volumes I have found useful at the bottom). Ultimately there’s no substitute for serious study over a longer period of time if you really want to understand the technical details of advanced physics, but as it stands, “The Biggest Ideas in the Universe” exemplifies Einstein’s quote that everything should be made as simple as possible, but no simpler. I’ll look forward to the next volume which is an account of quantum field theory.
Further reading: Here are a few volumes on relativity and especially its mathematics that I have found/continue to find helpful. Generally speaking, to understand relativity (including tensor calculus and differential geometry) one needs a decent background in vector analysis, calculus and differential equations and some linear algebra. Physics background includes basic classical mechanics and electromagnetism. But as Sean’s book shows, you can certainly understand many of the ideas semi-qualitatively without such formal background if you put in the time.
- Tristan Needham: Visual Differential Geometry – A gorgeous treatment of differential geometry that starts from scratch and really emphasizes the “geometry” in “differential geometry”. One of the pleasures of studying relativity is that it’s a fairly visual subject.
- Daniel Fleisch: A Student’s Guide to Vectors and Tensors – A clear account of vector analysis that starts with simple concepts and leads to tensors. There’s a particularly good discussion of covariant and contravariant vectors in here.
- Charles Misner, Kip Thorne, John Wheeler: Gravitation – Not a book but an encyclopedic door stopper of ideas from general relativity. “MTW” as it became known is kind of a multimedia extravaganza from the 70s, full of colorful pictures and cartoons. You dip into this book the way you dip into a plate of appetizers; it’s not really a textbook that you work through. Some basic ideas are explored with vivid analogies (for instance, the authors compare the challenge of measuring the curvature of spacetime to the challenge of measuring the curvature of an iceberg with a small rope tack from a boat).
- A. Zee: Einstein Gravity in a Nutshell – A very entertaining, idiosyncratic and informative treatment of relativity using fictitious dialogues between characters, historical stories and jokes which I have just started reading. Among other things, it provides an excellent account of metrics and how to calculate them.
- Edwin Taylor and John Wheeler: Spacetime Physics – Great introduction to special relativity.
- James Callahan: The Geometry of Spacetime – A good joint introduction to special and general relativity.
- George Joos: Theoretical Physics – An excellent general treatment of all kinds of basic physics topics and their underlying math.