by Jonathan Kujawa

The humble 2. It’s not big, like the Brobdingnagian numbers. It’s not nothing, like zero. It’s not the first something, like one. It’s hard to imagine much can be said about the unremarkable two.
Of course, Covid gave us a newfound appreciation for the power of exponential doubling. If you know of a novel disease and have 3 cases yesterday, 6 cases today, and are told to expect 12 cases tomorrow, it is quite something to predict close to zero new cases by April. But I’m just a simple mathematician who finds pulling random numbers from my rear end uncomfortable.
A happier, if apocryphal, tale is about the invention of chess. The story goes back to at least the 11th century: a clever courtier invents chess and presents it to their king. The king so loves the new game that he offers to give the courtier whatever they request. The courtier says that they’d like one piece of wheat for the first square of the chessboard, another two pieces for the second square, another four pieces for the third square, another 8 pieces for the fourth square, and so on for the 64 squares of an 8 x 8 chessboard.

18,446,744,073,709,551,615
grains of wheat for the courtier. That seems like a lot to count and you might rather weigh it out. Even then, it’ll be some work. After all, we’re talking about something like 18,446,744,000 metric tons.
A riddle loved and hated by students when they first learn about the prime numbers is: “What is the oddest prime?”. Sure to generate groans, the answer, of course, is two. Why the oddest? Being the only even prime makes two the black sheep among the primes.
On a questionably more serious note, the largest prime numbers are found using powers of two. As we talked about here at 3QD, last October the Great Internet Mersenne Prime Search announced that
2136279841-1
is the largest prime number known to humankind. It has 41,024,320 digits. Printing it out would take an 8,000 page book if you wanted to carry it around with you.

Given the massive amount of computational power needed to verify the above was a prime number, I can only marvel at Norman De Forest’s tour-de-force: “The Square Root of 4 to a Million Places“. Given that this calculation was done on the limited technology available at the time, it is no surprise the author offers a cautionary preface:
What follows are the first 1 million digits of the square root of 4. Actually, slightly more than 1 million digits are given here. These digits were computed by Norman De Forest using a custom utility and a command with a lot of dollar signs in the command line. They were computed during his copious spare time on a standard IBM PC over the course of about 6 minutes and 40 seconds. We do NOT guarantee the accuracy of these digits. Although these digits have been checked once we encourage others to check them as well. Please report any errors to “Norman L. De Forest” <[email protected]>.
— Norman L. De Forest
Mr. De Forest gives us another gift by providing a webpage from the early days of the internet. An era when the internet still had the simple naivete of a young technology full of promise. When you could share your interest in Tom Swiftes, and your virtual nemesis could be the Kellogg Corporation.
Speaking of square roots, the square root of two is a significant turning point in the history of mathematics. In the sixth century BCE the Pythagoreans of Ancient Greece discovered that √2 cannot be written as the ratio of two natural numbers. It was the first example of a number that undoubtedly exists in the real world and can’t be written as such a fraction. We know it exists because the Pythagorean theorem tells us it is the very real length of the diagonal in a square which has side length one.

For more on the math of this, see [3]. In what is surely another apocryphal story, the Pythagoreans supposedly tossed Hippasus to his death over the side of a ship for his discovery of this abomination.
Of course, you can’t put the genie back in the bottle. Once you know that the world contains non-fractions, you have to be dead inside not to be curious about what other numerical wonders lie out there. And, indeed, as we discussed here at 3QD, there are more real numbers than our minds can possibly comprehend.
“Square root of 2 is not equal to a/b,” noted Tom irrationally.
I recently learned of the following nifty puzzle:
Given exactly four instances of the digit 2 and some target natural number, use any mathematical operations to generate the target number with these 2s, using no other digits.
To avoid too much craziness, let’s agree that “mathematical operations” means the sort of operations we all see in high school. Things like addition, exponentiation, logarithms, trig functions, and the like. This is neither a riddle nor a trick.
For example,
1 = (2+2)(2-2),
2 = 2*(2)(2-2),
3 = 2+(2)(2-2),
4 = 2*2*(2/2),…
It’s fun to noodle on this puzzle during tedious work meetings. Pick a handy number, say 2025 or the largest known prime number, and try to write it using precisely four twos.
For years, this was a fun little challenge to throw at your friendly neighborhood mathematician to get them out of your hair. In the 1920s, the physicist Paul Dirac put his big brain on the problem and came up with a solution for all natural numbers. Namely, given a natural number n, you can always express it using logarithms and square roots via
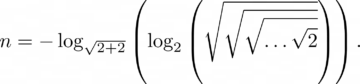
Here you should use exactly n square roots. For example,
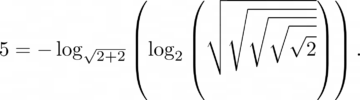
If you’d like to see how Dirac came up with this formula, check out this great blog post by Eli Bendersky. It was here that I first learned of Dirac’s technique.
A question that immediately comes to mind is if two is somehow special here. Can you do this with, say fours? The four fours puzzle, too, is an old problem that goes back to at least the 1800s. If you look at the Wikipedia link, you’ll find that you can solve it using a very Dirac-ish kind of solution. This suggests that maybe you can write any natural number using four copies of your favorite number between 1 and 9, whatever it might be.
As you might guess, there is a long history of people working on this and related problems. For similar topics, I recommend this Numberphile video. In it, Matt Parker talks about the work of Inder J. Taneja, a mathematician who is absolutely mad about these sorts of numerological puzzles.
It turns out that two holds more than a few surprises, after all!
[1] “I mean, it’s one banana, Michael. What could it cost? Ten dollars?”
[2] Image borrowed from Wikipedia.
[3] A natural number is a number from among 1,2,3,4,5,6,…. Until √2 came along, it was widely assumed that every number could be written as a fraction using these numbers (e.g., 1/2, 18/5, 11/3). One of the most powerful things about mathematics is our ability to prove that something is impossible. How? By imagining that it could be possible and then reasoning our way to something that can’t possibly be true. If our logic is sound, then the only escape is that we must have been wrong in supposing the thing was possible in the first place.
Here, suppose √2 = a/b for some natural numbers a and b. We can simplify by first canceling and eliminating as many 2’s from the a and b as we can. That leaves us with √2 = c/d, where one of c and d is an odd number. But then (√2)d = c and, squaring both sides, 2d² = c². Since 2 divides evenly into the left side, it must divide evenly into the right-hand side and, hence, must divide evenly into c. That means c is an even number and looks like c = 2k. But then we can substitute and do the algebra to get 2d² = (2k)² = 4k². Dividing by 2 gives us that d² = 2k². Once again, we can say that since 2 divides the right-hand side evenly, that means it evenly divides d. So, d is also an even number.
Wait! We reasoned our way to knowing that both c and d are even. But we already know one of them is odd. Since a natural number cannot be both even and odd, we must have gone wrong somewhere. Our logic is sound, so we must have been mistaken when we supposed we could write √2 as the ratio of two natural numbers.
***
Enjoying the content on 3QD? Help keep us going by donating now.
