by Jonathan Kujawa
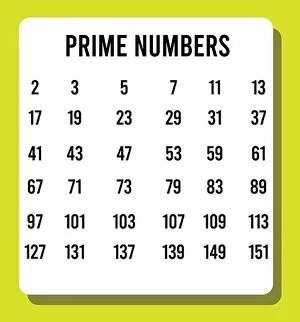 Prime numbers are the atoms of arithmetic. Just as a water molecule can be broken into two hydrogen and one oxygen atoms, 12 can be broken into two 2s and a 3. Indeed, the defining feature of a prime number is that it cannot be factored into a nontrivial product of two smaller numbers. Two primes that are easy to remember are
Prime numbers are the atoms of arithmetic. Just as a water molecule can be broken into two hydrogen and one oxygen atoms, 12 can be broken into two 2s and a 3. Indeed, the defining feature of a prime number is that it cannot be factored into a nontrivial product of two smaller numbers. Two primes that are easy to remember are
12345678910987654321
and
131211109876543212345678910111213.
Prime numbers are not only fundamental in mathematics, they are a key ingredient in the cryptography that secures your bank account, email, and everything else online. We can quickly and easily multiply numbers to get things like
1619890232090123459992473430408218409867740110001373,
but it is incredibly slow and difficult to factor a number like this into its constituent primes. The primes give us a mathematical lock that is easy to close and impossible to open unless you know how it was made.

Sadly, once again, the earthly rewards of mathematics elude us. For the purposes of cryptography, pseudoprime numbers are close enough. These non-prime numbers act like prime numbers in all the important ways for cryptography, and they are much easier to find.
Nevertheless, in math and computer science circles there was a flurry of excitement this week at the discovery of a new prime. Last week, the Great Internet Mersenne Prime Search announced that
2136279841 – 1 = 881694 … 86871551
is a prime number. The … is a yada yada of an awfully large number of digits. This new prime has 41,024,320 digits. That’s 16 million more digits than the second-largest known prime.
By comparison, AES-256 encryption is widely considered to be very secure, and it uses a key that is approximately 78 digits long. This prime is way too large to be of practical use. The goal is simply to find new prime numbers.
Why? George Mallory climbed Everest for the same reason: “because it’s there.” Unlike, say, the creators of livermorium, you don’t get to name a new prime number. But how can you not want to be one of the rare few who finds a new mathematical atom?
The goal of the Great Internet Mersenne Prime Search is to look for prime numbers of the form 2n – 1. A prime number of this kind is called a Mersenne Prime. We’ve long known that numbers like 2² – 1 = 3, 2³ – 1 = 7, 25 – 1 = 31, and more are prime numbers.

We believe that there are infinitely many Mersenne Primes. However, that remains an open question. Many numbers of the form 2n – 1 turn out to be non-prime. The one announced last week is only the fifty-second Mersenne prime we’ve found. If you’d like to join the search, the Great Internet Mersenne Prime Search provides downloadable software. There is even a modest cash prize for finding the next Mersenne prime!
This makes it seem like finding prime numbers comes down to mostly random luck. Indeed, a heuristic due to Cramér says that you can gain valuable insights into the prime numbers by treating them as if they are randomly distributed.
A famous open conjecture is that there are infinitely many twin primes. Two primes are “twins” if they are neighbors on the number line [2]. For example, 11 and 13 are twin primes. If the prime numbers were very regular, then you would expect there to be large gaps from one prime to the next. If the prime numbers are sprinkled at random, then some are going to end up clumped together. Cramér made a precise conjecture on the gaps between primes using this idea. While it seems that his conjecture is not quite right, the available data continues to support the heuristic that the primes are distributed randomly among all numbers.
Plot Twist! The prime numbers are completely determined. Here is a rule with the 26 input variables a through z:
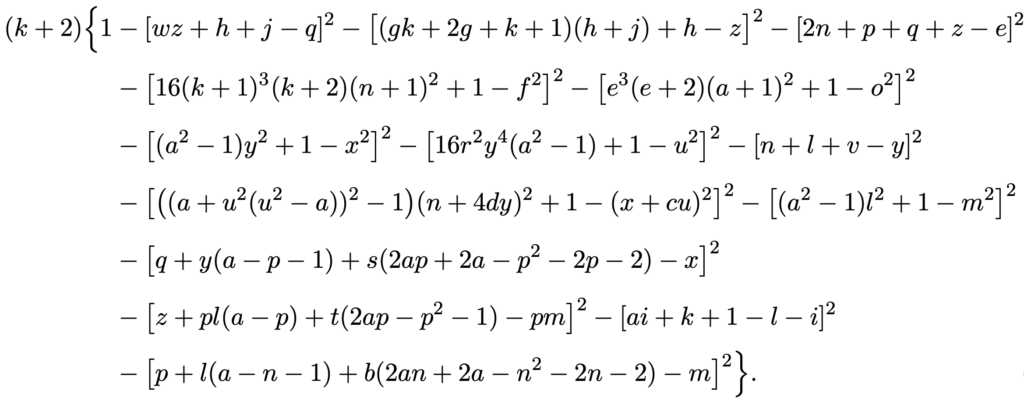
The result of Jones and company is part of a much larger story. We call a collection of counting numbers recursively enumerable if there is an algorithm that can print them out (possibly running without stopping if the collection is infinite).
 The Sieve of Eratosthenes from 2,500 years ago is an algorithm that generates the prime numbers. That makes the collection of prime numbers recursively enumerable. Thanks to the Lucas-Lehmer test, the Mersenne primes are also recursively enumerable.
The Sieve of Eratosthenes from 2,500 years ago is an algorithm that generates the prime numbers. That makes the collection of prime numbers recursively enumerable. Thanks to the Lucas-Lehmer test, the Mersenne primes are also recursively enumerable.
In 1970, Matiyasevich proved that if you give me a recursively enumerable collection of numbers, then there is a polynomial whose outputs are precisely that collection of numbers. Jones and collaborators found one of those polynomials for the collection of prime numbers. In separate work, Jones also found a polynomial that gives you exactly the Mersenne primes as the outputs:
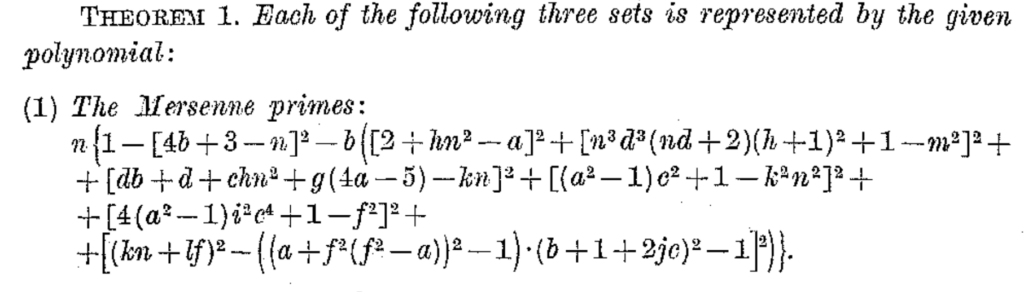
Jones gave us an explicit formula that computes the Mersenne prime numbers for us. Amazingly, we still can’t say if the Mersenne prime found last week is the last one, or if there are 1,000 more, or infinitely more. Sometimes, having an explicit description is still not enough to answer even simple questions.

Thinking about Mersenne primes reminded me of the 2048 game. It turns out to be the 10th anniversary. The creator released a new and improved online version that you can play. It’s as addictive as it ever was!
[0] The mathematician Richard Schwartz has devised a method for representing numbers as combinations of monsters. This image is borrowed from his website. His books are also great!
[1] Image borrowed from here.
[2] Remember that even numbers can’t be prime. The closest prime numbers can be on the number line is two apart.
[3] Image borrowed from the paper “What Can and Cannot Be Done with Diophantine Problems” by Yu. V. Matiyasevich.
[4] In fact, there is a whole collection of such polynomials. For example, Matiyasevich showed that you can find a polynomial that has only 10 input variables.
[5] Image borrowed from Jones’s paper.
Enjoying the content on 3QD? Help keep us going by donating now.
