by Jochen Szangolies

The ubiquity of a phenomenon sometimes causes its mystery to grow stale. Consider the strange lines along which a magnet orients iron filings in its vicinity: what we take in stride would, if experienced afresh, seem like the purest magic. Indeed, humble iron is probably the closest we get to genuine sci-fi ‘unobtainium’. Not only can the right treatment increase its durability by a multiple, enabling technologies unthinkable without it, but if you take a rod of iron, and hit it hard with a hammer, it suddenly acquires the ability to attract other bits of iron—as if the imparted force is transformed and stored in a mysterious field surrounding it. Moreover, if you then take that empowered core, and pass it through loops of very thinly wrought iron, you find that you can suddenly draw tiny bolts of lightning from the wire—or use the energy to power a light, or a motor, or, indeed, our civilization.
So, what is it that imbues iron with these near-magical capabilities? What yields it the power to attract or repel? Or, in the immortal words of the Insane Clown Posse, fucking magnets, how do they work?
Pace Violent J and Shaggy 2 Dope, the answer to this question is well known—in that particular sense of ‘well known’ that physicists use when they mean ‘don’t worry about it, the math says it works’. But even among physicists, the answer isn’t usually spelled out all that clearly—which is a bit of a shame: as we will see, it’s a cardinal example of how quantum mechanics, far from being just a ‘theory of the small’, is directly responsible for many everyday phenomena. Ultimately, the key to the question ‘why do magnets attract things’ lies in the phenomenon of quantum interference—though we’ll have to plot a bit of a roundabout course to get there.
Full Force Physics
Often, when talk turns to the quantum origins of forces, people start talking about the exchange of so-called virtual particles, which are exchanged between, say, two electrons. The analogy is that of two ice-skaters on the ice rink that throw a ball back and forth between them: with each throw, both attain a little bit of momentum in the opposite direction (recall Newton’s third law), and thus, move away from one another.
This seems fine, at first glance. Only, besides repulsive, force can also be attractive, leading to the skaters having to attain ‘negative’ momentum towards one another, exchanging particles of negative mass. Sometimes, it’s said that this is OK, because the particles involved aren’t real, but virtual; but then, it’s not really clear what the analogy actually provides us with, as far as an explanation is concerned. Moreover, virtual particles are themselves a troublesome concept: they really only occur as terms in an expansion series approximating the full physical phenomenon, and so are perhaps more of a mathematical bookkeeping device. So let’s just forget I ever mentioned them.
Instead, let’s go back to that perennial favorite of introductory quantum mechanics: the famed double-slit experiment. To recap, the double-slit experiment was designed to answer the question of whether light is a wave or a particle, to which the answer turned out to be ‘yes’. In fact, that’s the answer for everything!
What the experiment tests for is the phenomenon of interference: if troughs and peaks of waves impact one another, they cancel out; while all particles can do is pile up. So, a stream of particles directed at an aperture with two slits would be expected to produce merely the image of the two slits at a detector behind—two narrow bright bands. While a wave propagating through such a device would, due to differences in the path length from each of the slits to a given point on the screen, yield alternating dark and bright patches—an interference pattern.
Now, the mystery of the double-slit experiment is usually said to reside in the way quantum objects show both characteristics—while, say, individual electrons impact the screen one by one, each producing a nice, discrete dot, on the whole, the resulting pattern for sufficiently many produces the characteristic alternating pattern of interference. But for our purposes, it’s really just the interference we’ll be interested in.
So, why do the electrons interfere? Mathematically, the description of quantum objects involves somewhat unfamiliar quantities, the complex numbers. Complex numbers are produced by adding to the usual, ‘real’ numbers the so-called imaginary unit, ‘i’ for short, which has the property that i2 = -1. This, at first, is somewhat abstract, I grant. But there’s in fact a nicely intuitive way to make sense of these quantities that, curiously enough, will also turn out to be deeply related to the nature of the electromagnetic force: really, they’re nothing but rotations (in two dimensions).
To see this, consider that ordinary numbers can be thought of as stretchings: the number 3 is what you get if you take a unit-length stick and make it three times as long; ½ means contracting it to half its size; and so on. In this picture, the negative numbers then correspond to flips: taking 1 to -1 means flipping the rod over its left end. In combination, a negative number then is a flip and a stretch, so that ‘-π’, e.g., means to take your stick, flip it, and stretch it to roughly 3.14 times its size. Flipping an already-flipped stick returns it to its original orientation—hence, (-1)*(-1) = 1.
Now we see what the strange ‘i’ means: instead of flipping the stick fully, we just rotate it through 90°, so that it stands on its end. It’s now perpendicular to the usual number line—we have added a dimension to our numbers! Moreover, if we rotate it through another 90°, we have effectively flipped it—thus, i2 = i*i = -1. It turns out that this addition suffices to describe any combination of rotation and stretching in the plane. We can thus represent a complex number as a stick that has been rotated and stretched by a certain amount.
So far, we have only multiplied numbers, but we can also add them. What does an addition boil down to? Well, if you add two ordinary numbers, you can think of this as laying a stick the length of the first number end to end with one of the second. The same remains true with complex numbers, only now, the resulting stick may be shorter than either of the original ones. Hence, complex numbers can ‘reduce’, and even extinguish, one another—they don’t just pile up, like particles, but they can cancel out, like waves.
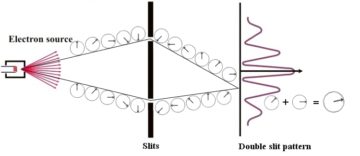
Indeed, we can describe interference by imagining a little rotating stick, like a clock hand, attached to every position along the trajectory of a particle. Wherever two trajectories meet, the result is the sum of both these little clock hands—which can cancel out, as well as reinforce each other. The brightness of the screen, it turns out, can be thought of as given by the size of the resulting stick (more accurately, the area of a given circle). Thus, to figure out whether we will see a bright or a dark band at a given spot on the screen, all we really need to do is count the number of rotations of the little clock hands along all the paths to get there.
Fearful Symmetry
Now consider what happens if we insert a device that somehow rotates the little stick—physicist speak of the ‘phase’—of everything that passes through. (Don’t worry how it does so.) If the phase is everywhere rotated by the same amount, that means that the relative orientation of the clock hands stays the same at any given point—but the relative orientation is what determines the length of the resulting stick, and with that, the brightness on the screen. Thus, the interference pattern is unchanged by such a global phase transformation—indeed, this transformation has no observable effect, at all: it is a symmetry of quantum mechanics.
Any operation that rotates the phase everywhere leaves observations invariant, just like a circle remains unchanged, no matter whether you turn it this way or that. Mathematicians call such a set of operations a group, and this particular one (for obvious reasons) the circle group; in physics, it is often referred to as ‘U(1)’, the group of unitary 1×1 matrices—that is, complex numbers of unit length.
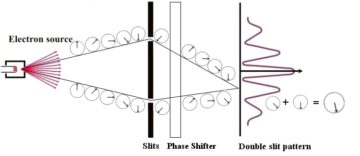
So, global rotations leave the interference pattern invariant. This is fine, as far as quantum mechanics goes, and our story could end here—but things become troublesome once we take into account that other pillar of 20th century physics, special relativity. There, ‘global’ notions are generally troublesome, because what ‘global’ means depends on the observer’s motion: the so-called ‘relativity of simultaneity’ means that observers in relative motion will disagree on what counts as ‘now’, as the present moment. Any transformation that acts everywhere simultaneously according to you will generally not do so for another observer. Hence, when incorporating relativity, we should really only look towards local notions as being physically meaningful.
Another, somewhat more technical, reason for considering local transformations is that they ensure local causality. There is a relationship between symmetries and conservation laws (think conservation of energy), first discovered by the German mathematician Emmy Noether, and consequently known as Noether’s Theorem. Essentially, any symmetry of a theory—such as the invariance under rotations we have discussed—entails that there is a quantity whose value does not change over time, i.e. is conserved. But for that to be true, it might be that this quantity—say, a particular amount of energy—vanishes here and reappears, instantaneously, on Mars. The total amount remains unchanged, but relativity sits uneasily with stuff going faster than light. A local symmetry, on the other hand, ensured that the corresponding conservation law is also local—that is, a conserved quantity, to pop up on Mars, first has to take the trouble of crossing all the space in between.
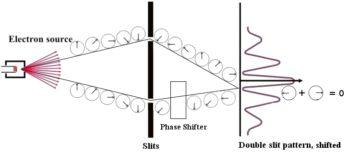
Hence, if we want to keep the phase symmetry of quantum mechanics, we better make it a local one. But here, we immediately run into trouble: once we transform the phase in the double-slit experiment only for a single path, the relative orientation of the little clock hands at the screen changes, and the interference pattern shifts. Quantum mechanics is not invariant under local phase transformations! But, as it turns out, there’s a clever trick we can do to keep this invariance—and that trick will lead us straight to electromagnetic forces.
Quantum’s Full Potential
But first, let us get back to the double-slit experiment. Let’s complicate matters somewhat: what happens if we add another slit to the setup? Well, to determine the brightness of any given spot at the screen, we now have to add up the contributions—putting the clock hands end to end—from three possible paths; no big deal. Likewise when adding a fourth slit, a fifth one, and so on.
Another complication we can introduce is to add another wall between the source and the screen, and put slits into that one, too: again, all we do is introduce more paths to sum, via every possible combination of slits. But suppose we carry this game through to its extreme, adding ever more walls with ever more slits: in the end, infinitely many walls with infinitely many slits just yield empty space again! That is, we can think of empty space as an infinity-slit experiment, with a slit at every point. But recall that to obtain the brightness at any given point, we have to sum over all possible slits to get there. Consequently, to obtain the ‘brightness’ at some point in space—the probability to find a given particle there—we likewise can sum over all possible paths to get there!
This is the germ of insight behind the so-called ‘path-integral formulation’ of quantum mechanics, due to Richard Feynman. Now, as noticed first by Paul Dirac, what determines the ‘clock rate’ of a quantum particle is the so-called action—a quantity of immense importance in classical mechanics. Indeed, almost all of classical physics can be recovered from the principle that all motion occurs along that path that minimizes the action—the aptly-named ‘least-action principle’.
In classical mechanics, this is something of a mystery: how does a system know in advance which path is the one that minimizes the action? But quantum mechanics now allows us to peek behind the curtain: suppose that the action for a path is small. Then, the action for the neighboring path won’t differ much. Consequently, the little clocks, along the paths, will have approximately the same orientation at the end points; thus, their sum will be large. On the other hand, for large action, neighboring paths will show higher variation in phase—the clocks will rotate faster. Hence, the difference in phases between neighboring paths will be large—and the resulting sum small. Again, interference is the answer: paths with small action tend to reinforce, while paths with large action cancel out. In the classical limit, then, the least-action path typically dominates.
But what is this mysterious action? For a simple case, such as a particle moving for some time with a certain amount of (kinetic) energy, it is just the energy times the time it has that energy. This means, for instance, that ‘wild’ paths, where a particle goes from A to B via some far-removed intermediary C, are disfavored: their action will be large, because to get there and back in time, the particle must move extremely fast, and thus, have a high kinetic energy, and a correspondingly large action.
While added kinetic energy increases the action, it can be decreased by introducing potential energy. Potential energy is the energy a system stores, e.g., due to its configuration—a ball, lifted up a certain way from the ground, has gravitational potential energy that is released—transformed into kinetic energy—when it is dropped. In such a process, the sum of kinetic and potential energy remains constant. Their difference then measures the ‘trade-off’ between the two; as potential energy depends on configuration, i.e. positions, and kinetic energy on velocity, this typically means motion—changing position with a certain speed.
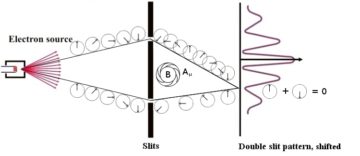
So, we can use potential energy to ‘re-balance’ the scales, to counteract the difference in action brought on by our local phase change. But what does this mean? In quantum mechanics, this is demonstrated by the Aharonov-Bohm effect, described in 1959 by Yakir Aharonov and David Bohm. If you place a long solenoid into the double-slit setup, even though the magnetic field (B) is zero outside of it, the interference pattern is shifted—because of the introduction of an electromagnetic potential (Aμ).
Thus, if we want to keep our local phase invariance, we can just add an appropriate electromagnetic potential, and recover the original interference pattern! In fact, it turns out that this is the unique solution to this problem: the requirement of local (U(1)-) phase invariance necessitates the introduction of an electromagnetic potential to compensate. Physicists, for historical reasons, refer to this procedure as a gauge transformation, with the resulting theory being a gauge theory.
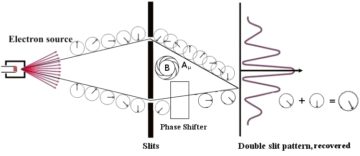
Consequently, from essentially just the requirement of local phase invariance and the phenomenon of quantum interference, we find we have to introduce a potential into the picture. But with a potential comes potential energy for everything that ‘feels’ that potential—in this case, every charged particle. But the introduction of potential energy, to keep the action minimal, means the introduction of kinetic energy to balance things out—which means, things start zooming around.
The quantum realm is something usually thought to be far removed from everyday experience, but once you start poking at things, you quickly find that you’ll have to drill down quite a bit to finally find explanations. But—and that’s the beauty of it—if you’re willing to stick with it, such explanations can often be found. So when next you ponder the mystery of the magnet, you now know that, ultimately, what you’re seeing is the result of the strange rules of quantum interference.
(Although… There is, actually, a little more to this. Magnets, specifically, also turn out to require a contribution from another theory that’s usually thought to be well-removed from everyday experience, consigned to the realm of the very fast—special relativity. But that’s a story for another time.)
