by Jochen Szangolies

Recently, the exponential growth of AI capabilities has been outpaced only by the exponential growth of breathless claims about their coming capabilities, with some arguing that performance on par with humans in every domain (artificial general intelligence or AGI) may only be seven months away, arriving by November of this year. My purpose in this article is to examine the plausibility of this claim, and, provided ‘AGI’ includes the ability to know what you’re talking about, find it wanting. I will do so by examining the work of British philosopher and logician Bertrand Russell—or more accurately, some objections raised against it.
Russell was a master of structure in more ways then one. His writing, the significance of which was recognized with the 1950 Nobel Prize in literature, is often a marvel of clarity and coherence; his magnum opus Principia Mathematica, co-written with his former teacher Alfred North Whitehead, sought to establish a firm foundation for mathematics in logic. But for our purposes, the most significant aspect of his work is his attempt to ground scientific knowledge in knowledge of structure—knowledge of relations between entities, as opposed to direct acquaintance with the entities themselves—and its failure as originally envisioned.
Structure, in everyday parlance, is a bit of an inexact term. A structure can be a building, a mechanism, a construct; it can refer to a particular aspect of something, like the structure of a painting or a piece of music; or it can refer to a set of rules governing a particular behavioral domain, like the structure of monastic life. We are interested in the logical notion of structure, where it refers to a particular collection of relations defined on a set of not further specified entities (its domain).
It is perhaps easiest to approach this notion by means of a couple of examples. Take the set of all your direct maternal ancestors: your mother, grandmother, great-grandmother, and so on. There is a relation that we might call ‘ancestrality’ that obtains between each two: your great-grandmother is ancestral to your grandmother, and your grandmother is ancestral to your mother. Furthermore, if Agatha is ancestral to Betty, then Betty can’t be ancestral to Agatha; and if Charlotte is ancestral to Dorothy, and Dorothy is ancestral to Eunice, then Charlotte is also ancestral to Eunice.
Now turn to your bookshelf. The books on it are of various thicknesses: Helgason’s Sixty Kilos of Sunshine is heftier than Williams’ Stoner, but both are dwarfed by Don Quixote. With a bit of thought, it becomes obvious that the thickness-relation between the books follows the same rules as the ancestrality-relation. Mathematicians formulate such rules in terms of axioms. If a, b, and c are arbitrary elements of either of the two sets, and we write suggestively < for the relation, then:
Nothing is ancestral to itself (not a < a)
Nothing is an ancestor of its own ancestor (if a < b, then not b < a)
The ancestor of an element’s ancestor is itself that element’s ancestor (if a < b and b < c then a < c)
For any two distinct elements, one must be the other’s ancestor (a < b or b < a if a and b are distinct)
The same rules work for the books on your shelf if we replace ‘is ancestral to’ with ‘is thicker than’. This means that the two sets have the same abstract structure (in this case, in mathematical terms, a strict total order). This is very useful: for suppose you’re engaged in a genealogy project, but are having trouble to keep the order of your ancestors straight. If you’re interested in n of your ancestors, all you have to do is take n books from your shelf, order them according to thickness, and fix a note to each spine corresponding to the name of one of your ancestors in order. Then, if you want to find out whether Mildred is an ancestor of Georgina, and the sticker labeled ‘Mildred’ is fixed to the back of One Hundred Years of Solitude while the one labeled ‘Georgina’ is taped to Kafka on the Shore, all you have to do is compare the thickness of the two books. A real time-saver!

This is the basis of scientific modeling. If you want to predict the behavior of one system, one way to do so is to take another system such that it instantiates the same structure, and map your observations on this model to the object under study, just as you mapped the books to your maternal ancestors. My favorite example is that of an orrery: because the little beads on wires are arranged in the same relative positions as the planets of the solar system, and because the gears that make it go implement the same ratios of movement, you can use the orrery to predict the motion of planets.
It is often useful to think about the instantiated structure in the abstract. Suppose we care only about three ancestors, respectively books. We may denote them, as before, a, b, and c; the entire collection is then the set {a, b, c}, the domain of the structure we are considering (the curly braces ‘{}’ here indicate nothing but a collection of various things, where what we can collect is left essentially open). We can then write somewhat more neutrally (a, b) for ‘a < b’, in order to not bias the interpretation of the relation we’re defining; this just means that ‘a is related to b’, in some not further specified way. For this, the parentheses ‘()’ denote an ordered collection, such that a is the first, and b is the second element of (a, b). In contrast, {a, b, c} has no ordering preference, so that it is the same object as {b, a, c} or {c, b, a}. Then, the relation can be fully defined by the set {(a, b), (b, c), (a, c)}; together with the domain {a, b, c}, it completely defines the structure we’re interested abstractly. This can be readily checked by testing it against the axioms above (exercise for the reader!).
Our abstract structure has two distinct concrete instantiations, in terms of books and ancestors. They might be, for example, {(Independent People, One Hundred Years of Solitude), (One Hundred Years of Solitude, Kafka on the Shore), (Independent People, Kafka on the Shore)} and {(Fiona, Mildred), (Mildred, Georgina), (Fiona, Georgina)}, over the domains (sets of elements) {Independent People, One Hundred Years of Solitude, Kafka on the Shore} and {Fiona, Mildred, Georgina}, respectively. These are then two different concrete structures, if the relation is interpreted as ‘is thicker than’ and ‘is ancestral to’, in turn. What this means is that there are multiple concrete structures that instantiate a given abstract structure: indeed, that’s ultimately what makes scientific modeling possible—by means of instantiating a system’s abstract structure in a model system, or by studying it abstractly, using mathematics (which lends itself to an interpretation of mathematics as the science that studies (possible) structures—but that only parenthetically).
The Paucity of Structure
Russell’s philosophical investigations were guided by what he called the problem of matter, which for him essentially meant the philosophical foundations of physics. He tackled the problem in a characteristically systematic—dare I say structured?—way. First, he set out to find a firm foundation for the language in which physical theory is written, namely, mathematics. The result of this investigation is the magisterial Principia Mathematica, which seeks to reduce mathematics uniquely to a logical foundation. Then, he sought to give an account of how we can come to have knowledge of the outside world. This resulted in his causal theory of perception. These set on firm foundations each, he went on to give a theory of the ontology of physics in terms of events and their connections, rather than, e.g., in terms of particles moving in space-time.
The project is as ambitious as it is sweeping in its reach, and is undertaken with Russell’s characteristic mix of precision, eloquence, and clarity. However, in its original form, it could never have worked: both of its preliminary investigations rest on foundations insufficient to bear the weight of their ambition. That’s not to say they were undertaken in vain: their failure, I think, has taught us something surprising about the world that might have been difficult to uncover otherwise, and it is perhaps only Russell’s penetrating logic that could have laid the underlying issues bare enough to uncover the crack in their foundations. Even today, it can still teach us new insights—such as, that Large Language Models (LLMs) have no way of knowing what they’re talking about.
In brief, what caused Russell’s project to stumble—twice—is that (abstract) structure underdetermines its domain. We’ve seen an example of this already: the abstract structure defined above does not determine whether it is instantiated in terms of books of varying thickness, or your maternal ancestral line. But of course, there was never really any reason to expect this structure to uniquely determine its domain.

But the question remains, can we do better? Can we find an abstract structure—a set of axioms, like 1.-4. above—that does single out a unique domain of applicability? This is what Russell and Whitehead attempted to do with the Principia Mathematica: find one single system that encompasses all of mathematics; one single set of axioms—an abstract structure—that would leave no questions open about its domain (what mathematical logicians call its ‘model’).
However, in 1931, the young logician Kurt Gödel proved his celebrated incompleteness theorems, the upshot of which is that every system of the type Russell advocated fails to establish some properties of its domain—that there are always multiple instantiations for any abstract structure, any set of axioms (of sufficient expressive strength). Just as 1.-4. fail to distinguish between books and ancestors, any attempt to fit mathematics within a single, strict structure always leaves enough ‘wriggle room’ to introduce different objects that still fulfill the structure’s strictures: certain questions about its domain are undecidable from the axioms. (A particular irony, here, is that the form of the argument used by Gödel—a so-called ‘diagonal proof’—closely parallels that of Russel’s paradox, which the latter had discovered lurking in the Foundations of Arithmetic of Gottlob Frege, who had himself tried to find a suitable foundation for mathematics.)
Virtually the same fate befell Russell’s causal theory of perception. Its central contention was that of the outside world, we only know the abstract structure; but as it turns out, such knowledge is a paltry thing indeed. Here, it was the mathematician Max Newman that pointed out the flaw in Russell’s formulations: if all we know about a domain is its abstract structure, then all we really know about that domain is the number of elements it contains (its cardinality). Why is that the case? Well, if I know that a particular structure exists, then I know that its domain exists. But I can create subsets of that domain at will—simply by defining appropriate groupings. But a collection of such subsets then is just another relation on that domain, and with that, defines another structure. So with the structure I am given, every structure on the domain exists. But every such structure already exists, if only the domain does. And as the elements of the domain are not further specified, the domain is entirely defined by the number of elements it contains.
Russell’s response to this criticism is what philosopher Stephen French has called a “classic Homer Simpson ‘Doh!’ moment”. A letter from Russell to Newman in response begins:
Many thanks for sending me the of-print of your article about me in Mind. I read it with great interest and some dismay. You make it entirely obvious that my statements to the effect that nothing is known about the physical world except its structure are either false or trivial, and I am somewhat ashamed at not having noticed the point for myself.
It should be noted here that it is the abstractness of structure that is at issue. If one allows instead acquaintance with (some) concrete structure, something like Russell’s view becomes more tenable (and there are some that interpret him as having put forward a theory of this sort, with Newman merely pointing out an ambiguity in Russell’s formulation). Philosophers often cash out abstract versus concrete structure in terms of extension versus intension. A relation is given in extension, if it is specified by means of enumerating all the elements that stand to each other in that relation; its intension is then what that relation is supposed to be—like listing all pairs of numbers such that one is smaller than the other as opposed to explaining the notion ‘smaller than’.
The Matter with LLMs
With the above, we are ready to assess the claims of LLM understanding—that, in some sense, LLMs know what they’re talking about, as opposed to being mere ‘stochastic parrots’ or ‘autocomplete on steroids’. The basic idea is that LLMs are in just the situation that all of us would be, if Russell’s theory of perception in its original form were apt—all they have access to is abstract structure, so, they can have virtually no knowledge of the domain.
LLMs are trained on a large corpus of texts. As such, all they have access to are words, or word-like entities including punctuation collectively called ‘tokens’, and the ways they are arranged. Now, some of these tokens denote things in the world, while the ways they are arranged amount to assertions about these—that is, relations over a certain domain given by the terms that refer to some concrete or abstract thing: a structure. A second layer of input is typically provided by human reinforcement—grading generated responses as regards their aptness.
The prototypical LLM task then is one of completing a partial relation—finding an element from the domain that fits in with the elements it has already been presented with (the prompt). In a vastly simplified way, suppose you are presented with a stack of books, ordered by thickness, and a stack of candidates to add to the pile: you would probably choose the next thickest book to complete the ‘prompt’. To do so, you need to have some abstract representation of the structure, that you take the stack to instantiate, and then complete with the appropriate token. This abstract representation, in the LLM, is essentially given by the weights defining its connectivity: it is those that ultimately implement the relation, having been set to their values by exposure to a large corpus of concrete instantiations of it (the texts they have been fed).
The question is, now: can just this act of relation-completion be indicative of understanding? Does knowing the abstract structure of language, in other words, suffice to glean the meaning of the terms present?
The prior considerations in this essay should make this seem dubious, but we can be more explicit. Adapting an example from Tim Button’s The Limits of Realism, suppose we have three sentences, ‘Ajax is a cat’, ‘Betty is a cat’, and ‘Chad is not a cat’. There, the denoting terms are ‘Ajax’, ‘Betty’, and ‘Chad’, making our domain {‘Ajax’, ‘Betty’, ‘Chad’}, together with a relation ‘…is a cat’ consisting of {(Ajax), (Betty)} (note that, in contrast to what we looked at before, this is a one-place relation—it is fulfilled by single elements, not pairs or multiples; but this doesn’t constitute a salient difference) [*].
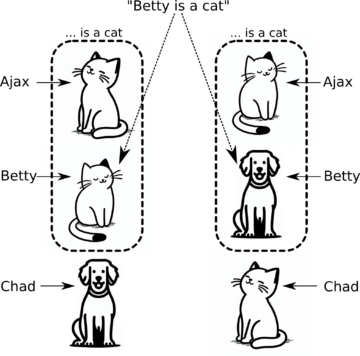
Now, when the LLM produces the utterance ‘Betty is a cat’, does it follow that it is speaking about Betty, who actually happens to be a cat? Well, no: the structure the LLM asserts has multiple different models, and there is no fact of the matter which of the models is the ‘right’ one. We can just ‘relabel’ the referents of the terms that are being used: we ‘cook up’ a new model, in which Betty is referred to be the name ‘Ajax’, Chad by the name ‘Betty’, and Ajax by the name ‘Chad’. Then, the relation ‘…is a cat’ is given by the set {(Betty), (Chad)}, and the sentence ‘Betty is a cat’ means that Chad is an element of this set—which is true. But Chad, of course, is not a cat—Ajax and Betty are. But the LLM is not talking about anything being a cat, as we understand it—it talks about a certain element fulfilling a given relation. In one model, that relation corresponds to sets of things that actually are cats, and the utterance names an element of that set—but in another, equivalent model, the relation does not map to cats, and what is asserted by the utterance may, while being just as true, not have anything to do with what we take its meaning to be.
Hence, there is no ultimate fact of the matter regarding what LLMs may mean—thus, if we take human utterances to generally have a definite (if maybe false) meaning, this human capability is beyond LLMs by virtue of their construction: the information they have access to, corresponding to mere abstract structure, is simply incapable of imparting them any nontrivial knowledge about the world.
[*] A point of clarification: I’m essentially granting the LLM, here, that it has figured out which tokens refer to elements of the domain, and which assert relations between these. Even this might be too much: essentially, any sentence can be thought of as a relation over tokens, and the LLM task being just to complete that particular relation. This doesn’t really map to anything in the world in particular, with the structure of language not necessarily reflecting the structure of the world; hence, I’m considerably simplifying the task the LLM faced in ‘understanding’ the world from the structure it has access to.
