by Jonathan Kujawa
A striking aspect of math is its ability to stimulate both our minds and our humanity. We saw this already in our discussion of Francis Su’s book, the Mathematics of Human Flourishing. As he explains more eloquently than I ever could, mathematics belongs with music, poetry, art, and nature in its ability to lift us up from the everyday mundane. Rather recently I learned of a perfect example I thought the readers of 3QD would appreciate. It’s a story that involves both neat mathematics and beautiful humanity.

The topic of the paper is continued fractions. As everyone knows, even if they’ve forgotten, we usually use write numbers using sums. For example, 327 is really shorthand for 300 + 20 + 7. And 0.327 is really shorthand for 3/10 + 2/100 + 7/1000. Of course, to capture all the numbers we are interested in using, we have to allow for infinite sums, even if that is sometimes a dangerous thing to do. For example, when we write
√2 = 1.41421356237…,
this is really a shorthand for
√2 = 1 + 4/10 + 1/100 + 4/1000 + 2/10000 + 1/1000000 + ….
But there is nothing sacrosanct about using repeated sums. We can also use repeated divisions. Once again you need to allow for infinitely many divisions to capture all the numbers we’d like to consider [1]. For example,
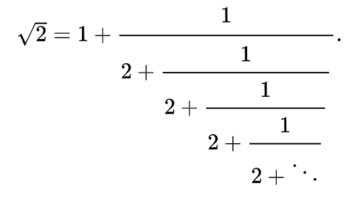
Like with sums, we’ve devised a more compact way of writing such continued fractions. Since we can always arrange so that the number above the division bar is a one, we can save ourselves work by only recording the number in front of the addition sign that appear at each level of the fraction. In this case, we would write [1, 2, 2, 2, 2, 2, …] for √2.
These mathematical gadgets have been of interest for centuries. They are often useful in both math and applications. You can use them for computing square roots, for example. Continued fractions also connect to dynamical systems and fractals by way of Minkowski’s Question Mark function. And, as we saw here on 3QD, John Conway showed us you can use them to determine when two knots are equivalent [2].
And, of course, they are interesting creatures in their own right! There are all sorts of fascinating questions you can ask about them.
For example, since a continued fraction usually goes on forever, you could wonder if two numbers eventually have the same continued fraction. That is, they may start out different, but if we wait long enough they have the sequence of numbers. For example, 1/√2 has continued fraction [0,1,2,2,2,2,…]. Even though √2 and 1/√2 aren’t the same numbers, they both have continued fractions which eventually agree (they’re both eventually a run of twos). For short, we call the tail what we get from a continued fraction by cutting off some of the numbers at the beginning [3].
It is a beautiful theorem by Serret which tells us when two continued fractions are eventually the same. Given four integers a,b,c,d and any number x, we can make a new number using the rule
![]()
Serret proved that the continued fraction for two numbers x and y have the same tail if and only if you can find four integers a,b,c,d which solve the above equation. Well, that’s a lie. Serret’s theorem also requires that the number ad-bc should equal one [4].
You can ask what happens if ad-bc is not equal to one. That brings us to the paper of Havens, Barbero, Cerruti, and Murru. They show that if x is a “nice” continued fraction and if ad-bc equals 2 or -2, and if you compute y by the above formula, then you can still predict the tail of y using the tail of x. Here a “nice” continued fraction means that it is either all evens, or all odds, or it alternates even, odd, even, odd, forever [5]. And you can take whatever you like for a,b,c,d, as long as the number ad-bc equals 2 or -2.
For example, x = (276 + √901)/25 has continued fraction [12, 4, 6, 2, 4, 6, 2, 4, 6, 2, …] and so is “nice”. The theorem of Havens, Barbero, Cerruti, and Murru predicts that the tail of y will be [… 8, 3, 4, 2, 12, 1, 8, 3, 4, 2, 12, 1, 8, 3, 4, 2, 12, …]. You could ask what happens if ad-bc equals, say, 3. This is certainly worth investigating, although the authors warn that their methods depend in strong ways on ad-bc equaling 2 or -2. You’ll need something extra to push further.

I promised at the beginning that this was a tale of both mathematics and humanity. So far, nothing we’ve seen suggests this story is any different than that of the dozens of research papers which appear every day. Until you search online and discover Christopher Havens’s mailing address is at the
Monroe Correctional Complex in Monroe, Washington. Christopher Havens is currently serving a 25-year sentence for murder.
Early on during his sentence, Mr. Havens spent a year in solitary confinement. He was desperate, of course, to stave off the loneliness and boredom of solitary. Somehow he stumbled across mathematics. Despite being a high school dropout who didn’t previously have much interest in math, its problem-solving and creative nature spoke to Mr. Havens. At first, he was self-taught. Later he connected with Umberto Cerruti and Luisella Caire, mathematicians in Italy, who gave direction to his studies. With their help, Mr. Havens discovered new results on continued fractions which, in turn, eventually led to the paper of this essay.
Mr. Havens plans to continue his studies, to serve his sentence, and to one day have a career and life in mathematics. Meanwhile, Mr. Havens started an organization, the Prison Math Project, to bring math to others in prison.

The Prison Math Project organizes in-person events and connects mathematical pen-pals. If you are interested in supporting these efforts, they welcome donors and volunteers.
While Christopher Havens committed a terrible crime that can never be undone, mathematics has put him on a new path.
What is justice? Is justice when we lock up a convicted killer and just have him serve out his time in misery where then he becomes a better criminal with the rest of the people who are living in their misery? Then they get out and they are not healed — they are still a danger to society. Wouldn’t it be better if we were able to become rehabilitated? And what if we wanted to be rehabilitated? We need to be able to have that opportunity to make those personal changes inside of us. And sometimes those personal changes, after all the scabs are peeled off, you eventually experience a couple of breaks in the clouds here and there. Mathematics has been that break in the clouds for me. — Christopher Havens
Last year the CBC had an interview with both Christopher Havens and Walker Blackwell, the co-founder of the Prison Math Project. I highly recommend taking the time to listen to it. The above quote is from that interview.
[1] One can drill down into the technicalities to make sure that doing so doesn’t rip the spacetime continuum. One can, but we won’t.
[2] Rest in Peace.
[3] A continued fraction actually has many tails since you can chop off the first number, or the first two numbers, or the first two hundred numbers, or… For our discussion, we’ll be a bit vague on how many numbers we chop off.
[4] If you happen to have taken linear algebra, you’ll recognize ad-bc as a determinant. That’s no accident! We are actually applying a matrix and the rule which calculates y is called a fractional linear transformation. There are close connections between linear algebra and number theory and geometry, with fractional linear transformations acting as the bridge between the three. It would take us too far afield, but it’s worth at least mentioning that the relevant geometry is the utterly strange hyperbolic geometry.
[5] Odd, even, odd, even, odd, even, forever is equally okay.
[6] Image borrowed from the Prison Math Project.
[7] Image borrowed from the CBC.
