by Jonathan Kujawa
According to Johns Hopkins University, as of this writing, 315,023 people worldwide have died from Covid-19. One of those 315,023 was the incomparable John H. Conway.

At the age of 82 and with health issues, Conway was well within what the CDC euphemistically describes as “people who are at higher risk”. It was perhaps not unexpected that someday soon he would no longer be with us, but it was a shock to the mathematical world, nonetheless. Conway’s mathematical powers, irreverent style, and forceful personality made him a well-known and seemingly permanent feature of the mathematical community for more than sixty years.
When I was a graduate student twenty or so years ago, John Conway came to my university to give a series of lectures. Like many math departments, we had an endowed fund to bring in eminent visitors who were well regarded as both researchers and speakers. In our case, the standard format was for two talks: one for undergraduates and one for the faculty. In truth, this more often ended up being one for graduate students and faculty, and one for specialists. Not surprisingly, many mathematicians aren’t the greatest at making their talks accessible.
As the OG mathemagician, Conway had no trouble being accessible, interesting, and entertaining. That said, I must confess that I have only the dimmest recollection of the talks themselves. But I do remember the talks for a quintessentially Conway reason.
At the time the department had an honorary T-shirt which was given to speakers as part of the introductory activities. Nearly every speaker made the same joke. Without fail they would chuckle and ask if they were to put the T-shirt on immediately. We would politely laugh as if we hadn’t heard the same joke told by the previous week’s speaker.
Conway being Conway, he skipped right to the punchline and beyond. Conway stripped off his shirt, strode barechested across the stage in front the entire math department, pulled the T-shirt on, and dove straight into the beginning of his first lecture.
Conway was known for his ability to turn play into serious mathematics, and serious mathematics into play. While his Ph.D. was in logic, Conway’s interests were wide-ranging and often focused on seemingly non-serious topics like games, knots, puzzles, geometry, and the like.
In honor of Conway’s passing, I thought it would be appropriate to share a few of my favorite Conway-isms. If you’d like to hear more, I recommend reading Martin Gardner’s essays about Conway’s work. Devoted 3QD readers will recall that Martin Gardner wrote a column in Scientific American about recreational math. Conway’s playful approach to mathematics made him and Gardner natural partners. Mathematics’ Butch Cassidy and the Sundance Kid (without the shootout at the end). In that 3QD essay I talked about the game of Sprouts. It was invented by Conway and popularized by Gardner in one of his columns. Sprouts is classic Conway: a seemingly silly game whose rules have been carefully crafted to unlock rich gameplay and rich mathematics.
Closer to my own areas of research, Conway made important contributions to the field of group theory. In mathematics, a “group” is a collection of symmetries for some object [1]. For example, a circle has infinitely many different possible rotations which leave it unchanged, while a square has only four such rotations. Since the symmetries of an object often tell you a great deal about the object, it is no surprise that group theory is widely used in math, physics, chemistry, and biology.
A simple group is a group which cannot be built from two smaller groups. They are the “atoms” of group theory. All groups are built from simple groups. In this metaphor, a group is a molecule and it is built up from its constituent simple groups [2]. It is a natural to want a complete classification of the simple groups. A periodic table, if you will.
Groups were first introduced by Galois in the 1830s in his study of the solvability of equations. We talked about his work here at 3QD, although I kept the group theory hidden in that essay. For more than a century, a periodic table of simple groups was a fool’s dream.
In the 1960s a series of breakthroughs in group theory suddenly made the classification a plausible goal. In 1972 Daniel Gorenstein gave a roadmap for how to achieve a complete periodic table for the simple groups. In the end, it turns out that there are three families of simple groups which each have infinitely many members and an additional 26 “sporadic” simple groups. The sporadic groups are anomalous and don’t seem to fit any particular pattern.
How do you go about classifying mathematical objects? You do it by proving that everything which could exist, does exist. That is, you come at it from two sides. You have to prove results which exclude all but a specific list of possibilities, and then you have to prove that those possibilities do, in fact, exist.
It is much like the recent discovery of the Higgs boson. Using reasoning you squeeze what is possible into an ever-smaller box. You squeeze until you describe it so well you are sure it must exist and, more importantly, you know where to look and how to find it. Then, with luck, you find it where the calculations said it would be.
Group theorists in the 1960s-1980s worked with maximum force on both sides of the classification. A series of results by many researchers ran to tens of thousands of pages of mathematics. Their calculations eliminated many potential simple groups and gave precise descriptions of the ones which remained. Coming from the other side, researchers tried to explicitly build these putative groups as the symmetries of some object (often a geometric object).
This is where Conway comes in. His powerful computational skills coupled with his strong geometry intuition gave him the ability to construct simple groups as the symmetries of geometric objects. This was a heady time. If you were clever and knew where to look, you could discover a new simple group. Like discovering a new element, doing so was a result for the ages.
Last year here at 3QD we ran across the Leech lattice. This is an ultra symmetric geometric object which lives in 24 dimensions. Because it has a ridiculously large number of symmetries, it is reasonable to hope that new simple groups might appear as the symmetries of the Leech lattice.
In 1968 Conway did exactly this! In fact, there are three simple groups which are symmetries of the Leech lattice and which weren’t known before. These three groups are now and forevermore known as the Conway groups, with the largest having 4,157,776,806,543,360,000 elements.

Let me mention one other important contribution by Conway to group theory. It is known as Monstrous Moonshine. The largest of the sporadic simple groups is known as the Monster. Building on a numerical observation of John McKay, Conway and Simon Norton conjectured that there should be a deep relationship between the Monster and the seemingly unconnected world of modular forms and number theory. When we discussed sphere packing here and here at 3QD, we saw there is a close interplay between the symmetries of a lattice and number theory. Monstrous Moonshine was one of the first hints at this deep connection.
While reading Siobhan Roberts’ entertaining biography of John Conway, “Genius at Play,” I learned of another delightful Conway invention [3]. It is a Turing complete programing language called FRACTRAN [4]. In FRACTRAN a program is a list of fractions and the program is run by starting with a single integer and following some simple rules.
For example, here is a list of fractions which constitute a program in FRACTRAN:
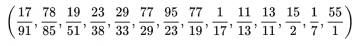
Here is the rule for how to run this program. Start with 2. Going from left to right, find the first fraction which becomes a whole number when multiplied by 2. In this case, it is 15/2. Multiplying by 2 yields 15. Taking 15, repeat the process. The first fraction which can be multiplied by 15 and yield a whole number is 55/1, which yields 825. Taking 825, repeat this process. The first fraction which can be multiplied by 825 and yield a whole number is 29/33, which yields 725. Continuing in this way we build up a list of numbers:
2, 15, 825, 725, ….
If you compute long enough, you will eventually hit numbers which are exactly powers of 2. For example, after 19 steps you’ll hit 2²=4. Grinding along, eventually you hit 2³, then 25, 27, 211, 213,…
If you have an eye for patterns, you might recognize the list 2, 3, 5, 11, 13, ….. Amazingly, Conway’s FRACTRAN program computes the prime numbers. Since FRACTRAN is Turing complete, it can calculate anything you like. With a list of just 40 fractions, Conway was able to write a FRACTRAN program that computes the digits of π!
I have to admit this is completely mysterious to me. How is it that such a short list of fractions and a simple set of rules can compute things as complicated as the primes and π? One of my summer projects is to learn the ins and outs of FRACTRAN.
FRACTRAN is the sort of simplicity, play, depth, and richness that Conway was known for. Conway showed us how complicated the world really is. Or maybe he showed us how simple the world really is? Or, maybe he showed us the world is both.
Let me end with one more Conway-ism. Morley’s Theorem states that, for any triangle, if for each angle you draw the pairs of straight lines which trisect the angle, then the points where these lines intersect always forms a triangle with three equal sides (aka an equilateral triangle). Conway gave a beautiful, elementary, geometric proof of Morley’s Theorem.

Conway also discovered a beautiful theorem about triangles which could have been from Euclid himself. See Colm Mulcahy’s webpage or Matt Baker’s blog for details and for links to Conway’s many other gems. Better yet, you can watch John Conway on Numberphile if you’d like to hear about his work from the master himself.
John Conway was a true original. He will be missed!
[1] If you happened to have learned of groups, you might recall them as having a rather abstract definition. If your professor was uninspired, symmetries may seem only distantly related to groups. But Cayley’s Theorem tells us every group is the symmetries of some object. Indeed, as a representation theorist, I would stand on any group theorist’s kitchen table and declare that symmetries are the proper way to think of any group.
[2] To be careful, I should say that I am only thinking of groups that have finitely many symmetries. Which means the rotations of the circle are out for this discussion. If you allow for infinitely many symmetries in your group, then the story gets more complicated.
[3] Roberts’ book is a quick and entertaining read. It’s highly recommended. It has a rather unusual style. It swings between contemporary conversations with Conway and discussions of history and of his mathematical works. Readers wanting a dispassionate, linear history may be disappointed, but those wanting a taste of the verve and creativity which was John Conway will be in for a treat. It reminds me of Feynman’s autobiographies. Which is about right. Conway seems to have been as much a self-mythologist as Feynman.
[4] Turing complete means that it is a programing language that allows you to run any possible algorithm and, indeed, any program at all. This means your web browser could, in principle, be programmed and run in FRACTRAN.
