by Jochen Szangolies
This is the fourth part of a series on dual-process psychology and its significance for our image of the world. Previous parts: 1) The Lobster and the Octopus, 2) The Dolphin and the Wasp, and 3) The Reindeer and the Ape
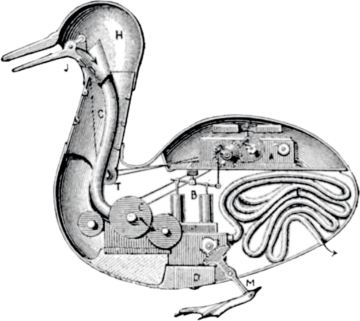
A (nowadays surely—or hopefully—outdated) view, associated with Descartes, represents animals as little more than physical automata (la bête machine), reacting to stimuli by means of mechanical responses. Devoid of soul or spirit, they are little more than threads of physical causation briefly made flesh.
It might perhaps be considered a sort of irony that the modern age has seen an attack on Descartes’ position from both ends: while coming to the gradual realization that animals just may have rich inner lives of their own, a position that sees human nature and experience to be entirely explicable within a mechanical paradigm, going back to La Mettrie’s 1747 extension of Descartes’ view to humans with L’Homme Machine, has likewise been gaining popularity.
This series, so far, can be seen as a sort of synkretistic take on the question: within us, there is both a rule-based, step-by-step, inferential process of conscious reasoning, as well as an automatic, fast, heuristic and unconscious process of immediate judgment. These are, in dual-process psychology, most often simply referred to as (in that order) ‘System 2’ and ‘System 1’.
In my more colorful (if perhaps not necessarily any more helpful) terminology, System 2 is the lobster: separated from the outside world by a hard shell, it is the Cartesian rational ego, the dualistic self, analyzing the world with its claws, taking it apart down to its smallest constituents.
System 1, on the other hand, is the octopus: more fluid, it takes the environment within itself, becomes part of it, is always ‘outside in the world’, never entirely separate from it, experiencing it by being within it, bearing its likeness. The octopus, then, is the nondual foundation upon which the lobster’s analytic capacities are ultimately founded: without it, the lobster would be fully isolated from the exterior within its shell, the Cartesian homunculus sitting in the darkness of our crania without so much as a window to look out of.
Philosophy in the Tension of Analysis and Intuition
In the 20th century, philosophy took the ‘linguistic turn’: inspired by the Positivist’s focus on empirical matters of fact as the sole source of truth—a program of which one of its leading proponents, A. J. Ayer, later claimed that its greatest defect was that nearly all of it was false—the philosophy of language turned to analyzing supposedly metaphysical problems instead as issues of imprecise or misused language.
In the broadest sense, it consists of a shift of focus: rather than considering the difficulties ‘to understand how things in the broadest possible sense of the term hang together in the broadest possible sense of the term’, in Wilfried Sellar’s phrasing, to be due to the things and their obstinate refusal to hang together in a sensible way, blame may be shifted instead to our means, or mode, of understanding—such that problems of our conceptualization of the world get mistakenly projected out into the world.
The hope was, then, to unmask many of the traditional problems of philosophy as ‘pseudo-problems’, which can be solved by a more careful application of sufficiently precise language—echoing the Leibnizian dream of finding a ‘characteristica universalis’, a universal formal language, by means of which any philosophical problem could be answered due to the action of a ‘calculus ratiocinator’, a rule system such that any problem posed to it could be solved by means of calculation. Then, any philosophical dispute would be solved by an exhortation of ‘Calculemus!’ (‘Let us calculate!’).
Sadly—or perhaps, fortunately, for those who suspect such a mechanical world would be entirely too lacking in intrigue, mystery, and adventure—that dream, in its most starkly formal realization, died a spectacular death in 1930. That year, at a conference in Königsberg attended by many mathematical luminaries of the day, 25 year old logician Kurt Gödel presented his celebrated incompleteness theorems; thus showing that the program of finding a definite, consistent axiomatization sufficient to derive all mathematical truths, most closely associated with the mathematician David Hilbert, can never be completed. There is no perfect language suitable for expressing all and only that which is true.
But even if this final extreme of the program can never be completed, I believe there is something right about its general aim, and this series has been my sketch of how a careful consideration of dual system psychology might aid its goals.
The thread of argumentation, as developed so far, runs like this. The world is not present to us as-is, as it might be to the dolphin, capable of recreating ultrasound images, and thus, accessing the shape of things themselves. Rather, we must rely on symbolic referents, which take the place of objects in the world within our understanding, much like words take the place of things in text.
But we are not, like (arguably) the sphex wasp, mere rule-based automata, doomed to simple repeat application of the same procedures to the same inputs. We create models of the world that are fluid, open to revision, that evolve and adapt—but that nevertheless must not be confused with the things they model. This modeling, I believe, depends crucially on an interaction between the two systems—with the octopodal System 1 providing the entrance of the world within the mind, while the conceptualization engine of the lobsterian System 2 proceeds to parcel it up into neat concepts, to be organized, like Lego bricks, into the world as it appears to us (our ‘lifeworld’).
In this process, we are subject to bias and error twice: one lies in the fact that the world never appears to us unvarnished, that all data comes to us only as filtered by our senses—as in the reindeer’s marvelous adaptation changing its eye color in the winter, to gather more light, and thus, ‘brighten up’ a darkened world.
The other source of error is more subtle. It helps to think of System 1 as working, in outline, like a neural network: a classification engine, sorting inputs into different classes. However, its reasons for doing so are often opaque—this is a formal issue: in general, an algorithm equaling a neural network’s performance by means of explicit comparison (if…then…else-like step-by-step evaluation) will be a vast and ungainly thing, not easily apprehended at once. But with nothing but the neural network’s judgments, each of our intuitions about the worlds would ultimately be incomparable—we judge something to be a cat because it looks, inscrutably, cat-ish.
For a social ape, this will not do. It would lock us into disjoint, separate worlds, with no means of connection between one another. Language—or, at a deeper level, concepts and reasons—is then a means to bridge this gap. We may use an analogy from physics and think of our different concepts as different coordinatizations of the world—different ways to organize its contents, as they appear to us. Language, then, ideally, provides coordinate transforms between your world, and mine. But this view leaves something out: language didn’t evolve as an impartial mediator, but rather, to convince, to justify, and perhaps even deceive.
It is this melange that makes the finding out of ‘how things hang together’ so fraught with difficulty: we are each locked within our lifeworlds, which get amalgamated into one social reality by a tool that has, at best, been coopted for the job, and all the while run the danger of mistaking our lifeworld for the world as such, and hence, believing everyone who disagrees to simply be wrong. The fracturing of this social world, as many perceive to happen now, then seems not so hard to explain—indeed, it seems a miracle that it doesn’t happen more often (or even, that we manage to find some measure of common ground at all).
But I think there is a positive moral to this story, as well, and in many ways, it is this that prompted me to embark on the writing of this series. For if we know of the above biases and influences on our judgment, those who do not agree with us need not be branded irrational, or even stupid. Indeed, continuing the analogy from physics, there, only propositions that are coordinate independent are ultimately meaningful. The absolute position, or velocity, of an object does not have any importance—but relative positions and velocities do. Thus, we should aim not to anchor our views within our own, idiosyncratic, lifeworld-bubble, but instead, locate them in the web of relations between us and others, strengthening, rather than weakening, the coherence of the social world.
In the remainder of this article, I will propose some brief sketches regarding how the view developed so far may be usefully turned to classical philosophical problems. These problems may be, with some justification, considered academic; they are certainly not the most pressing we are presented with today. But I think they are a useful proving ground for the methods implied by the above. Of course, I do not presume to present solutions to these issues, but sometimes, a new way to think about an old problem can itself be useful.
Heaps of Universals
So let’s start with a classic. A red sportscar and a red dinner plate have something in common; but what, exactly, is it? What is redness beyond the car being red and the dinner plate being red? Is it something that exists in itself, with each particular somehow partaking of its essence? Or is it merely a category into which we lump certain things?
This is, of course, the problem of universals (put briefly). Plato believed universals to exist beyond the objects of the physical world; his most famous student, Aristotle, held that they exist only insofar as they are instantiated in the real world.

There seems to be an easy answer to this problem, as given by the ‘two systems’-view: whatever is similar is lumped into one and the same bin by the neural network-like System 1, just as an image recognition software might group pictures according to ‘shows a cat’ and ‘does not show a cat’. But this would be getting ahead of ourselves: we are still presuming some objective characteristic that some of these pictures have (‘catness’), which others lack. Hence, nothing really has been won!
There is a way around this, though: rather than presuming that our neural network-like classification engine groups things together because of their similarity, let us take heed of the lessons of the previous installment of this series, and hence, invert this reasoning: things appear similar because they are grouped together. Put starkly, there are not really cats and non-cats out there in the world, because ‘catness’ is not a property of things in the world, but of things in the lifeworld.
This might seem difficult to accept, at first. But I believe it gets more easily palatable when we remind ourselves of what the great constructivist Heinz von Foerster called the ‘Principle of Undifferentiated Coding’: the brain does not perceive sounds, lights, or smells; rather, neuron activity merely codes the intensity, but not the nature of the stimuli they receive. All the brain has to work with, then, are neuron spike trains of varying frequency. If there were such a thing as ‘catness’ out there in the world, it would be very difficult to see how it could be transported by these spike trains—certainly, they do not partake in ‘catness’ themselves.
The categories of the world then are ultimately elements of the lifeworld, not of things out there. What is then ultimately open to discovery is not how well they map onto the world, but how well my categories map onto yours—to discover their relative, rather than absolute, position, and thus uncover a coordinate-invariant truth, so to speak.
This strategy works for other, similar problems, as well. Consider the Sorites-paradox: a heap, when one grain of sand is removed, remains a heap; but if you continue removing grains, at some point, you end up with something that is decidedly not a heap—perhaps a few grains, perhaps even a single one.
Here, too, we should not accept heaps as things out there in the world, where what is and isn’t a heap is open to discovery. We classify things as heaps, and it may not be the case that for every heap so classified, they remain a heap under removing grains. System 2 loves a sharp category, but System 1 is more flexible, and assigns levels of certainty.
This tolerance towards vagueness has more general applicability. A classical analysis, originating with Plato, has it that knowledge is justified, true belief: what you believe with good reason, if it happens to be true, is what you know. But in 1963, Edmund Gettier challenged this account, by pointing out that there are situations in which you may have justified true belief, yet which we wouldn’t consider instances of knowledge.
Consider the following. You sit in a crowded café (ah, remember when that was a thing?), and hear your cellphone’s ringtone. This is justification for your belief that somebody is calling you. You pick up, and sure enough, your mother is on the other end of the line. Hence, your justified belief turned out true.
However, unbeknownst to you, your cellphone was actually set to silent, and you heard another guest’s, who coincidentally had the same ringtone: even though you were right about being called, the evidence that convinced you did not actually support this belief.
So what, then, is knowledge? In the wake of the Gettier problems, ever more strict definitions were offered, and ever more elaborate counterexamples found. David Chalmers, in Constructing the World, notes that there were conjunctions of no less than fourteen terms, seeking to nail down knowledge—yet still being found wanting.
Perhaps, then, it’s just unknowable what knowing amounts to? I think the lesson of this failure to define knowledge is quite different. For the striking thing is that, whenever a new counterexample is offered, we are, in fact, able to recognize it as such—hence, whatever definition of knowledge we’re using is not the one involving the fourteen-clause conjunction just refuted. We must have some knowledge of what knowledge is, independently of that definition, or else, we could never realize cases fitting that definition which nevertheless aren’t instances of knowledge.
But from the two-systems point of view, this is readily explicable. It is just what we would expect if the concept of knowledge is a System 1-judgment, while its definition is a System 2-algorithm: in general, the latter can capture the former only incompletely. But then again, the problem of knowledge is not one of the world, but of our relation to it—of our coordinatization of the world into distinct, monophyletic concepts.
This lesson, I think, applies more generally. Just because we don’t have an exhaustive, bullet-point definition of a concept, doesn’t necessarily mean we don’t understand it—indeed, if we didn’t, how could we ever know if the bullet-point list was apt?
Again, I do not presume that the story ends here. But I hope that what these examples do is show that there’s some legs to the two-systems view: that it can profitably be applied to yield new perspectives on old problems. My aim in this series then wasn’t to arrive at any answers; instead, I will have achieved my goal if some who read this may come away from it feeling that they have gained a new asset in their toolkit for chipping away at the issue of how things do, indeed, hang together.
