by Jochen Szangolies
This is the third part of a series on dual-process psychology and its significance for our image of the world. Previous parts: 1) The Lobster and the Octopus and 2) The Dolphin and the Wasp
Rudolph, the blue-eyed reindeer

With Christmas season still twinkling in the rear view mirror, images of reindeer, most commonly in mid-flight pulling Santa’s sled, are still fresh on our minds. However, as the Christmas classic The Physics of Santa Claus helpfully points out, no known species of reindeer can, in fact, fly.
That may be so. But reindeer possess another superpower, one that sets them apart from all other known mammals—once the frosty season sets in, their eyes change color, from a deep golden-brown to a vibrant blue (to the best of my knowledge, there are, however, no reports of unusual colors related to the olfactory organs). The reason for this change of color has long been a mystery, until a study by Glen Jeffery and colleagues from the University College London pinpointed a likely reason in 2013: the change in hue serves to better collect light in the dark of winter.
When we think of eye color, we typically think of the color of the iris—but for some mammals, cats most familiarly, another factor is the tapetum lucidum, a reflective layer behind the retina. Due to its color change, reindeer eyes are able to gather more light—thus, the lack of light is offset by an increased capacity to utilize it. The world outside gets darker, but the world the reindeer see, the world they inhabit—their lifeworld, in Husserl’s terminology—may not, or at least, not as much.
The world comes to mind through the lens of the senses. The lifeworld is never just an unvarnished reality, nor even an approximation to it—it is the world as transformed in our experience. A change in this lifeworld then may herald both a change in the world, as such, as well as a change in our perception—or reception—of it.
This is not mere filtering: while the particulars of our senses mean that we cannot, for instance, see ultraviolet light, the lifeworld is not a just a neutral sampling of the information in the world. Rather, brains construct models of the world in a predictive fashion—perception is a creative process. That’s why we’re so prone to see patterns in noise—which makes good sense, evolutionarily speaking: better to see a tiger where there is none than to miss the one ready to pounce.
This construction is a typical System 1 activity: it happens without conscious effort, automatically, and nearly immediately. It is also an activity that is difficult to cast in terms of clear-cut rules. This is typical of neural networks: it is, in general, hard to give a simple set of criteria for a neural net’s judgments. This lends them an air of inscrutability: a neural net may be great at sorting pictures into cats and non-cats, but its reasons, as such, remain often opaque.
Confounding Neural Nets
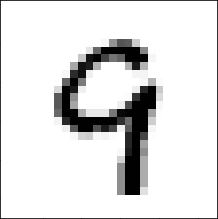
A standard task to evaluate neural net performance is built on the so-called MNIST dataset, consisting of labeled handwritten numbers. You use some portion of these to train a neural net, and then test it on the rest to assess its abilities in classifying them.
The neural net has 784 input neurons, each of which ‘looks at’ a single pixel of an input image. The (greyscale) color of this pixel is translated into a number between zero and one, giving the neuron’s activation level; by means of a ‘hidden’ layer of neurons, this input gets transformed into the activation level of ten ‘output’ neurons, representing the numbers 0 – 9. The level of activation of each output neuron represents the net’s ‘certainty’ that the corresponding number is shown in the image.
Some time ago, I was interested in what, exactly, the neural net is ‘looking for’ in making its judgments, so I basically let it run in reverse—essentially, letting it come up with a sort of ‘ideal’ notion of each number (this, in a much more sophisticated way, is somewhat like how neural networks can create artificial faces and the like).

The result is shown in Fig. 3. And sure enough, if that image is fed to my neural net, it is identified as the number 9 with 98% certainty.
It might be objected that all I did was code up a crappy neural net. And well, that’s true, to an extent. But it did actually rather well at its assigned task—identifying the correct number about 95% of the time. The problem is, rather, that it ultimately doesn’t know what a digit is supposed to look like—it has no concept of ‘digit’. To it, there are just various kinds of grayscale blobs that it has been told belong to certain categories. It indiscriminately extends its classification to any such picture whatsoever, and what ends up being categorized as ‘9’ does not necessarily align with our concept of the digit ‘9’—the blob in Fig. 3 looks just as nine-y to it as the one in Fig. 2.
In a world where every picture, every stimulus it receives, falls neatly into the category ‘digit’, it succeeds at its task; but once that world is enlarged to include non-digit stimuli, it flounders, in a—to us—bizarre way.
But these ‘errors’ are not necessarily so far removed from human cognition as one might think. We are heavily disposed to referring to something in terms not directly applicable to it—think of phrases like ‘a warm color’: color does not have a temperature—indeed, color is not the sort of thing ‘having a temperature’ applies to. Yet, we readily associate orange or red with warmth, and blue with cold: is this, ultimately, so different from associating the above grayscale blob with nine-ness? From calling a melody joyful, a sip of wine dry? Indeed, from feeling the same ineffable awe when regarding a Mark Rothko painting as one does faced with the sublime beauty of a mountainous landscape?
These might all be examples of the same general phenomenon: a classifying system—say, tasked originally with labeling objects as falling on a spectrum of temperature—being applied to data outside of its ‘comfort zone’, so to speak, and being just as pleased with a warm ochre as with the comforting warmth of the hearth.
Moreover, these judgments seem to have some claim towards universality. Consider the two shapes in Fig. 3. One of them is called ‘Kiki’, and the other ‘Bouba’. If you had to guess, which is which?

Surprisingly—or, maybe not—attitudes towards the correct association of names to shapes are remarkably consistent across distinct linguistic communities. If the above is right, then this might be the result of the same classifying system responsible for categorizing sounds, if met with visual input, putting the spiky shape in the same ‘bin’ as the sound ‘Kiki’, and grouping ‘Bouba’ with the rounded form.
But what is important here is to note that we have not thereby unearthed a deep truth about the world—there is no inherent ‘kikiness’ to spiky shapes, nor ‘boubaness’ to rounded ones—not anymore than there is nine-ness to the above gray blob. The truths of the lifeworld are not necessarily truths of the world ‘as such’—yet, they are truths (and frequently important ones) all the same. We should not succumb to the temptation of mistaking the map for the territory—of, in other words, concluding that because we judge the spiky shape to be Kiki, this necessarily means that it is Kiki. A hypothetical alien with a different internal wiring might come to the exact opposite judgment—with this being just as much an intriguing truth about its lifeworld as it is about ours.
Another common element between these sorts of judgments is that they’re typically hard to explicate clearly—we call the spiky shape ‘Kiki’, but we’re hard-pressed to explain why; likewise, it is hard to precisely enunciate why a Rothko painting moves us the way it does (not that this hasn’t been tried, exhaustively). This is just a consequence of the fact that typically, translating the categorizations of a neural network into clear, step-by-step rules—in other words, bringing System 1 into a System 2-mold—is a difficult problem.
Social Cohesion, the Engine of Reason
But for a social animal, this clearly won’t do: because while judgments as the above may be universal to a certain degree, there will nevertheless always be differences. And what good would it do to be left with incompatible judgments, but no way to adjudicate between them? How do you convince anybody that, no, the rounded shape is clearly ‘Bouba’ when they don’t share that opinion, and all you have to marshalin your support is its ineffable boubaness?
A tool is needed to mediate between incompatible judgments—to convince your neural net, your System 1, that it makes a mistake when sorting the rounded shape into the ‘Kiki’-bin, I need to be able to build a convincing case: I need to lay out arguments, from shared premises, leading, via a System 2-process of step-by-step inferences, to the inexorable conclusion that, no, that shape is actually Bouba. The tool to do so is something that is present, in this form, only in that strangest of the great apes, homo sapiens sapiens: language.
With language comes reasoning, and with reasoning come reasons—no longer content with, say, a particular gray blob looking nine-y, we want to know why. And that’s where the trouble starts.
Language demands a shared basis, shared conventions for the meaning of certain sounds or symbols—shared concepts. But the world does not neatly decompose into distinct concepts. Hence, we are faced with a certain arbitrariness—there are different possible ways of conceptualizing the world.
The Greek poet and philosopher Xenophanes was one of the first great naturalizers: recognizing that most supposed gods share the distinct characteristics of those believing in them, he proposed a natural origin to many phenomena. About the rainbow, associated with the messenger goddess Iris, he thus wrote:
And she whom they call Iris, this too is by nature a cloud.
Purple, red, and greenish-yellow to behold.
This deflation of the mystical nature of the rainbow might not quite hit its target, but it is striking for another reason: Xenophanes delineates the color spectrum of the rainbow into just three distinct color bands—in the original Greek, porphúreos, phoiníkeos, and chlorós.

This seems odd from our point of view: typical modern presentations will subdivide the rainbow into six or seven distinct colors (the latter going back to Newton’s color scheme). In Fig. 5, I have attempted to illustrate the distinction—although, and this is indicative of the larger problem, I felt that wherever I tried to delineate each color, I seemed to have just missed its ‘true’ boundary.
Indeed, the ancient Greeks sometimes seem to have had a weird take on color—Homer, for instance, famously wrote about the ‘wine-dark sea’. This has on occasion led to unfortunate misunderstandings—ranging from the benign belief that the Greeks lacked a word for blue to the curious idea that they somehow couldn’t see blue, at least not the way we do. Indeed, the starkest reading of the so-called Sapir-Whorf hypothesis claims that the ancient Greeks could not see blue because they had no word for blue: that lacking the word, and hence, the concept, the thing itself cannot figure in their lifeworld.
The Sapir-Whorf hypothesis also goes by the name ‘linguistic relativity’, and broadly speaking refers to the idea that the structure of language influences the cognition of its speakers. In its weakest forms, it seems almost trivially true—what we cannot put into concepts, we may well have difficulty thinking about—while its strongest readings, that language wholly determines what can be thought, are easy to repeal: just think about all the times you have struggled to express your thoughts verbally—if language where the sole determinant of thought, then thought would be intrinsically verbal.
But, as so very often, it’s the fraught territory in between the extremes where the interesting stuff happens. While it may not be true that your language determines which colors you can see, differences in language can lead to differences in performance in sorting colors (He et al, 2019). In this sense, language might be seen as a set of conceptual tools, which may be more or less well-suited to a given task.
Language, and the concepts it imbues us with, then, may be something evolved to perform a certain function—and according to the thesis of Mercier and Sperber discussed briefly in the first part of this series, that function may be largely concerned with social cohesion. But performing that function well does not necessarily imbue its concepts with any claim of truthfulness: concepts may be useful, without thereby necessarily being faithful.
In a lecture entitled ‘Is there an Artificial God?’, Douglas Adams illustrates this by means of Feng Shui, which—according to him—invites us to arrange our home such that a dragon could pass through unhindered. Now, even if there are no more dragons than there are flying reindeer, this may not be a useless exercise: it may be that we can indeed find pleasing arrangements of furniture and such in this way.
Let us thus suppose that Feng Shui—or the above caricature of it—works as advertised. It is then, I think, the key error of human reason that because this concept works to well, it has to get something right about the world—to put it bluntly, to conclude the existence of dragons from their conceptual usefulness.
From a formal logical point of view, this is just the fallacy of affirming the consequent—we stipulate ‘if A, then B’, observe B, and hence, conclude that A must be the case. Put in such starkly formal terms, it seems hard to believe that anybody would reason this way—from ‘if I have been in the rain, I am wet’ and ‘I am wet’, it does not follow that I have been in the rain: I could’ve had a shower, or gone for a swim, or lost a water balloon fight.
Yet still, I believe it is much more common than we typically acknowledge. It is the mistake we make whenever we suppose that an element of our models of the world—of our lifeworld—must faithfully track something out there, in the world as such.
Taken to its extremes, this view, when challenged by different conceptualizations of the world, must retreat into essentialism: into supposing that my concepts are the true, objectively applicable ones, while yours are just mistaken—that the spiky form really is Kiki, and everybody believing differently is simply wrong. In particular regarding color vision, this argument has indeed often been made.
William Gladstone, 19th century British Prime Minister, thus feels moved to confidently declare, after reviewing color terms present in Homer:
Now we must at once be struck with the poverty of the list which has just been given, upon comparing it with our own list of primary colours, which has been determined for us by Nature [my emphasis]
He then proceeds to give the list of seven colors, as per Newton: the Greeks were wrong, but thankfully, Newton since read the true list of colors off of Nature herself.
We have seen that the world is shaped twice before becoming the lifeworld: once, through the constructive mediation of the senses, and again, through the conceptualization of System 2’s reasoning engine. Failing to realize this, we project the elements of our lifeworld out into the world as such, holding them as its objective structure—and often, being met with great puzzles as a result.
This may seem a disappointing conclusion: is then the end result of this train of thought mere constructivism—is all that we consider true merely a figment of our imagination, albeit perhaps a useful one? I don’t think so: the account provides us with unique resources to resist this threat of radical skepticism. The ground work for this was laid in the previous part of this series—there, it was argued that the self and the world emerge together in a kind of ‘splitting’, somewhat in the way the colors of the rainbow emerge from splitting white light into its constituents. But in doing so, each retains something of the structure of the other.
Teasing this out properly, however, will require a little more elaboration.
