Superdeterminism: Quantum Mechanics Demystified Or The End Of Science?

by Jochen Szangolies

The quantum world, according to the latest science, is, like, really weird. Cats that are both dead and alive, particles tunnel through impenetrable walls, Heisenberg can’t both tell you where he is and how fast he’s going, and spooky influences connect systems instantaneously across vast distances. So it seems that anything that serves to reduce this weirdness should be a godsend—a way to bring some order to the quantum madness.

Superdeterminism, its advocates say, provides just this: a way for every quantum system to have definite properties at all times, without instantaneous influences—and no cats need to come to harm. All we have to do is to give up on one single, insignificant assumption: that our choice of measurement is, in general, independent of the system measured.

Yet, belief in superdeterminism has so far remained a marginal stance, with the vast majority of scientists and philosophers remaining firmly opposed, sometimes going so far as to assert that accepting superdeterminism entails throwing out the entire enterprise of science wholesale. But what, exactly, is superdeterminism, why should we want it, and why does it polarize so much?

The story starts, as so much in the foundations of quantum mechanics does, with Bell’s theorem. I’ve written on that topic at some length before, but a quick refresher will serve to lay the groundwork for what’s to come.

All The Bells And Whistles

The table above shows a set of measurable quantities, A₁, A₂, B₁ and B₂, their possible values (each +1 or -1), and the probability p_i with which the ith configuration of values obtains. In short, what Bell’s theorem then says is this: if this table exists, then the CHSH-quantity (named after physicists John Clauser, Michael Horne, Abner Shimony and Richard Holt)

can never exceed a maximum value of 2. Conversely, if we find a value in excess of 2, then such a table is impossible.

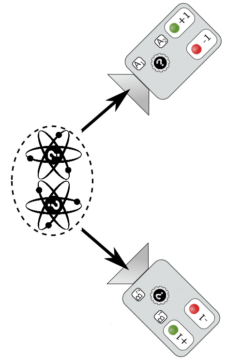
Now, most discussions of Bell’s result start somewhat differently—but mathematically, the above is the very core, albeit specialized to a particular setting. To make contact with the more common exposition, we start with Alice and Bob, two intrepid physicists out to prove a point. They engineer the following setup: each of them procures one half of a physical system—say, each has one of a pair of particles—and then, they move far away from each other—far enough such that no signal traveling at light speed could cross the distance between them over the duration of the experiment.

This requirement ensures locality: if physics is local, nothing Alice does can influence what happens at Bob’s lab during the experiment, and vice versa. Each of the pair has now at their disposal a pair of measurement apparatuses, labeled A₁ and A₂ for Alice, and B₁ and B₂ for Bob, respectively. It does not really matter for our purposes what these devices measure—perhaps position and momentum, or particle spin in different directions. The only salient fact is that each outcome will always be either of +1 or -1.

A series of measurements, performed on a series of identically prepared particle pairs, will thus produce a series of +1 and -1-values for each of the different measurements, with each of the possible outcomes—the lines in the above table—occurring some number of times. Dividing through the total number of experiments then yields the relative frequency of each line, each configuration of values; and with enough repetitions, that will come to approximate the probability of any particular outcome.

To make this a little more concrete, suppose you carry out 10,000 experiments, and obtain the outcome (+1,-1,+1,-1), or just (+-+-) for short, 3578 times. Then, you conclude that the probability of obtaining that outcome—p₆ in the table—must be approximately 0.36, or 36%.

In a classical world, you could then just proceed and refine your estimates for each of the probabilities in the table by performing more and more measurements—Alice measuring A₁ and A₂, Bob measuring B₁ and B₂ in each round on their part of the system. But quantum mechanics throws a spanner into the works: in general, two measurements on the same system can’t be performed together. What this means is that, if Alice measures A₁, then A₂, and then A₁ again, the repeated measurement’s result doesn’t necessarily agree with the one obtained in the first round. Measuring A₂ effectively ‘invalidates’ the information gathered from measuring A₁. (This is nothing but Heisenberg’s uncertainty.)

Thus, Alice and Bob can’t simply check whether the table exists. But each of Alice’s measurements can be performed together with each of Bob’s—anything else would already entail a violation of locality. That means they can measure each of the terms in the CHSH-expression above: a quantity like ‘C(A₁, B₁)’ denotes the correlation between A₁ and B₁—it is equal to 1 if both values always agree, equal to -1 if they always disagree, and somewhere in between for less-than-perfect correlation. If it is 0, then the value of A₁ tells you nothing about B₁. (Mathematically, it is the expectation value of the product of both, and can be calculated simply by adding up all the probabilities for those outcomes where both values agree, and subtracting those where they disagree.)

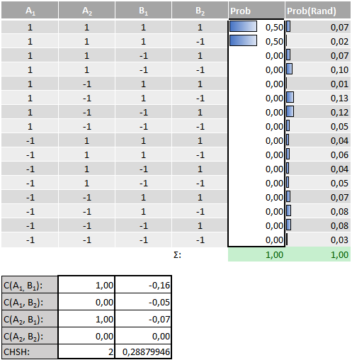
With this, it can be shown that, for any distribution of values for the probabilities of the different options, the CHSH-expression can never exceed a value of 2. I won’t give a proof here (for a sketch, see the previous column), but I’ve prepared an Excel-file that you’re encouraged to play around with. In it, you’ll find a version of the above table, where you can enter the probabilities for each of the possible outcomes or configurations yourself. If you enter a valid probability distribution (all values are between 0 and 1 and sum to 1), it will calculate the value of the CHSH-expression for you, as well as all of the correlations that enter into it. One thing to try is just to enter a 1 into any given row, and 0 in all of the others: the value of the CHSH-quantity will be 2. It’s then not hard to convince yourself that you can never find a combination that exceeds that value, since each is just a combination of such cases with coefficients that sum to 1.

Consequently, whenever the table above exists, the CHSH-quantity can at most equal 2. The table is an expression of realism: all measurable quantities have a definite value, whether they’re measured or not, and each combination of such values is present with a certain probability. Each measurement then just reveals a preexisting value. Conversely, it seems it must be the case that if the table does not exist, then there can be no fixed assignment of values to all quantities!

Enter Superdeterminism

As so often, the devil is in the details. What we have assumed above is that our probing has no effect on the probability distribution we’re investigating—i.e. that it is the same, no matter what measurements Alice and Bob perform. The second sheet of the Excel-file shows what may happen if we relax that assumption: rather than each set of measurements sampling from one probability distribution, we will now allow for there being a different distribution for each combined set of measurements—that is, for the probabilities to be different if Alice and Bob measure A₁ and B₂ than if they measure A₂ and B₂, for example. The following table looks at the example in more detail.

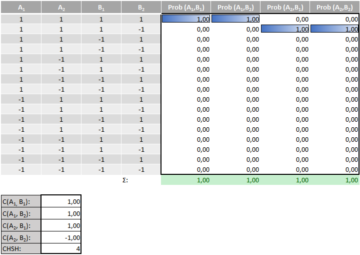
In this example, whenever Alice and Bob measure the pairs (A₁, B₁) or (A₁, B₂), every value is +1; however, when they measure the pairs (A₂, B₂) or (A₂, B₁), the value of B₂ is -1, instead. That means that the first three terms in the CHSH-expression are equal to 1 (each A is equal to each B), but the final term is equal to -1 (A₂ and B₂ are opposite to one another). Since that term is subtracted, the total value is 4—violating the bound. (This value also exceeds the quantum mechanical value of 2∙√2; why this value is the quantum maximum, rather than 4, is an object of ongoing research, but need not bother us here.)

Now, how can such a situation come about? One reason would be that Alice’s measurement choice influences Bob’s result: whenever she measures A₁, Bob will observe the value 1 for B₂; in contrast, when she measures A₂, the preexisting value for B₂ is -1. This is a violation of locality: Alice’s actions have an instantaneous effect on Bob’s side. Thus the usual gloss of Bell’s theorem: no local realistic theory can recapitulate the predictions of quantum mechanics. If somebody tells you they have a local realistic (and non-superdeterministic) theory equivalent to quantum mechanics, ask them to produce the values to enter into the first table: if they can’t, then their theory does not fit the bill.

But there’s another way to view matters: whenever the combination of values is (+++-), Alice will always carry out a measurement of A₂. She is thus not free to choose what to measure: her choice is (super-)determined. Then, too, the value for the CHSH-quantity will be 4; but neither locality nor realism are threatened.

Now, superdeterminism is really a misnomer: Alice and Bob are not any more determined than in any garden-variety deterministic theory. All that they do, under strict determinism, is fixed by the state of the universe at some point prior (perhaps at the beginning, in its initial conditions), including their ‘choices’ of measurement—they could not act differently than they actually do. What changes under superdeterminism is that things are set up such that, in the example, the values (+++-) and the measurement of A₂ always co-occur. There is what Leibniz called a ‘prestabilized harmony’ between the values and the measurement choices. Thus, it isn’t in any sense more deterministic than ordinary determinism; it’s just that things are determined such as to feature special correlations between measurements and preexisting values. This means that, contrary to some discussions, there are no greater difficulties for free will in a superdeterministic world than are already present in an ordinary deterministic one—hence, we need not further bother with this topic (which I have covered elsewhere).

Thus, it seems that, contrary to what’s sometimes presented in popular accounts, we can have a local theory of definite, preexisting values after all—at nothing but the expense of introducing some correlations between our measurement choices and their outcomes. So why isn’t this the preferred solution?

Is The Moon There When Nobody Looks?

The reason that superdeterminism has not hitherto managed to attract a large following is that many scientists (and philosophers of science) feel that accepting it calls into question the foundations of science itself, making the whole thing a self-refuting endeavor. This was perhaps first made explicit in a 1976 article of Shimony, Horne, and Clauser, three of the letters in CHSH:

In any scientific experiment in which two or more variables are supposed to be randomly selected, one can always conjecture that some factor in the overlap of the backwards light cones has controlled the presumably random choices. But, we maintain, skepticism of this sort will essentially dismiss all results of scientific experimentation. Unless we proceed under the assumption that hidden conspiracies of this sort do not occur, we have abandoned in advance the whole enterprise of discovering the laws of nature by experimentation.

Accepting superdeterminism then would be a case of throwing the baby out with the bathwater: saving locality at the cost of dumping the whole of science. But recently, resistance against this conclusion has been forming, most notably thanks to physicist and science communicator Sabine Hossenfelder, climate physicist and Oxford emeritus professor Tim Palmer, and their co-authors.

In particular, Hossenfelder has tackled the objection in a form proposed by, among others, philosopher of science Tim Maudlin, founder and director of the John Bell Institute for the Foundations of Physics. Suppose that a study finds a strong correlation between smoking and cancer in laboratory experiments with rats. Ordinarily, we would take this as evidence towards a link between the two. But now enter the superdeterminist tobacco lobbyist, arguing that the random selection process dividing rats into the group exposed to tobacco smoke and the control group was predetermined such that rats already predisposed to develop cancer ended up predominantly in the former group. Thus, the choice of exposing certain rats to tobacco smoke was already correlated with their predisposition to develop cancer—hence, we can’t conclude anything about tobacco’s carcinogenic properties.

Against this, Hossenfelder mounts a two-pronged defense. Her first angle of attack is to focus on the justification for rejecting superdeterminism (or, what amounts to the same thing, using the assumption of ‘statistical independence’ of measurements and observed values). We assume that our measurements are independent of the measured values in macroscopic settings because, simply, it works—our theories derived on the basis of this assumption hold explanatory power. But that doesn’t entail that this continues to be the case in the quantum realm. Furthermore, quantum violations of independence are unlikely, she claims, to yield classical/macroscopic violations, because the process of decoherence ought to tend to ‘wash out’ such effects on sufficiently large scales.

This second part of the argument seems immediately somewhat spurious: decoherence is, after all, a quantum effect; but quantum effects are ultimately just due to the particular correlations between measurements and preexisting values. Thus, appealing to decoherence to explain the absence of superdeterminism in the large is ultimately to appeal to superdeterminism again—which is then just to say that it’s part of our superdetermined world that no superdeterminism exists on the large scale. But this has no explanatory force: all it says is that measurements on certain, quantum, systems are superdetermined to correlate with the existing values, while those on other, classical, systems are not so determined. This is merely a stipulation of brute fact.

But it’s the first prong of the argument that I find more troubling. In a word, Hossenfelder alleges that statistical independence is merely a pragmatic principle, whereas it is actually a methodological one. To tease this apart, we need to take a brief look at what science, and empirical observation, is ultimately for.

The photograph series “The Horse in Motion”, by Eadweard Muybridge, was commissioned by businessman and racehorse owner Leland Stanford to settle a bet: he held that the four legs of a horse during gallop, for a brief moment too fleeting to see with the naked eye, all simultaneously left the ground. Muybridge’s photos showed that this is indeed the case, thus settling the bet, and becoming a classic in both photography and the scientific study of animal locomotion.

But note the character of the question being asked. What Stanford contended was that no matter what, during galloping, the horses legs are airborne; but what Muybridge demonstrated is only that they are when the horse is photographed at the same time. For Stanford to win the bet then needs commitment to another premise: that what is observed under controlled conditions indicates what occurs absent any observation. But this is the premise called into question by superdeterminism.

Or take another example. Whenever I lift my eyes towards a certain patch in the sky during a certain time, I will see the moon. What patch this is and when to look can be predicted by a simple rule. I would thus want to conclude that there is something like the moon, and it follows a particular orbit. This is the simplest way to make sense of my observations—it is an example of abductive reasoning, or inference to the best explanation. But in a superdeterministic world, it might be that the moon randomly fluctuates in and out of existence, and it just so happens that my instances of looking coincide with its being at the expected spot.

This is not just a frivolous example, because ultimately, such abduction is at the heart of our ability to make predictions in science. Consider, for instance, me trying to gauge the distance to the moon by means of a laser, rather than looking at it. Under ordinary assumptions, I could be confident that my laser will impinge on the moon and be reflected, since I am confident that the moon is there no matter what. But in a superdeterministic world, that my looking is correlated with the moon’s being in no way entails that so is the laser’s firing. Hence, I loose the ability to generalize away from the context of my own observations—but this ability is integral to the business of making scientific predictions.

Certainly, one could write down a theory on which the moon’s existence not just correlates with my own looking, but also, with the laser firing. But the point is that my own observations, without the assumption of independence between my looking and the moon’s being there, give me no reason whatsoever to believe in this theory. That the laser will find the moon where I expect it to be is justified by my observations only upon making the assumption that this being there is not just contingent on my looking.

Indeed, if we assume perfect correlation between me looking and the moon being there—that is, the moon is there if and only if I look—then seeing the moon tells me exactly nothing but the fact that I am looking (which however I already know). There is no information gathered from this observation. It’s as with pairs of socks in different drawers: if you find the right sock in one, that the corresponding one in the other must be a left sock tells you no new information.

This seems to be a general consequence of superdeterministic models. To see this, we can look at an explicit example of such a model, capable of reproducing the predictions of quantum mechanics, proposed by a team of physicists from the National University of Mexico. Their idea is as simple as it is compelling: to produce a local model capable or reproducing the quantum predictions, we simply take a deterministic, but nonlocal model (such as the Bohmian formulation), and let every point in spacetime behave the way the corresponding point in the model does. Effectively, you adduce a simulation of the entire universe to each point, and then have every point calculate what happens in this simulation, and behave accordingly.

This fulfills the desiderata of a superdeterministic model: measurements and values will always emulate those in the Bohmian setting, and thus, yield the ordinary quantum predictions; however, no superluminal influences are necessary. We again have a perfect preestablished harmony: every point carries within it the history of the entire universe, and thus, all act perfectly in concert.

But this is also the model’s greatest downside. For in a model of this kind, there is never any true interaction; no measurement yields any information; no hypotheses about the behavior of the rest of the universe have any validity. For no matter how any given object behaves, no matter what happens at any given spacetime point, things would not be affected by completely removing the rest of the universe. Hence, whatever happens at a given point, happens no matter what goes on anywhere else. But then, any observation of a given quantity does not, in fact, tell us anything about the system under study; indeed, it does not even tell us whether there is such a system at all, since no matter its existence, our measurement apparatus, and our experience of that apparatus’ reading, would be exactly the same.

In this sense, a superdeterminist world collapses into solipsism: whatever happens in the rest of the universe, or even whether there is such a ‘rest of the universe’, has no bearing on my own experiences. The world is a collection of Leibniz’ ‘windowless monads’, without any possibility of interacting, or exchanging information. The locality superdeterminism saves is absolute: nothing knows anything about what goes on at even the slightest separation.

Now, it may be objected that these conclusions are just based on one particular superdeterminist model. But a recent theorem seems to suggest that it is, in fact, a generic consequence: in order to recapitulate the quantum predictions, superdeterminism must be total—for any amount of independence between measurement settings and outcomes, there exists a quantum experiment such that its predictions won’t be fulfilled. What this means is that the hidden parameters each quantum system carries around must have complete information about all measurements and interactions it will ever partake in—given this information, nothing is up to chance. But then, any such interaction does not actually ‘tell’ the system anything new—as above, it can just play out its prerecorded program, and again the world decomposes into isolated threads unspooling regardless of what occurs elsewhere.

The acceptance of superdeterminism then is far from the mere rejection of a pragmatic principle whose usefulness has run its course. In rejecting the possibility of generalizing beyond any given measurement context, it robs us of a shared, connected world, and decomposes the universe into a patchwork of isolated, local stories of which nothing can be known safe our own. However much we might long for the resolution of the quantum mystery, superdeterminism is the kind of answer that negates the object of the question.