by Jochen Szangolies

Whenever I use words like ‘reality’, ‘truth’, or ‘existence’, I feel an almost irresistible urge to mark my vague sense of unease by liberal application of scare quotes. After all, what could such words even mean? They seem to denote concepts too vast and simultaneously slippery to be pinned down by a simple denotative term. Like trying to point at everything all at once, such terms seem to cast so wide a net that they fail to single out any one thing in particular.
There is, I think, a good reason for this unease, and modern science is beginning to reveal the contours of it—and with that, some of its own limitations. In the previous column, I have argued that the typical starting point for science, conventionally understood, is the existence of an independent world that we can approximate ever more closely in our knowledge of it. There is a subject-object distinction baked into it that delineates this process neatly into questions of epistemology, of what we can know and how we can know it, and ontology, of what there is. According to this story, a subject with the right epistemological tools can uncover the objective ontology of the world through patient and painstaking labor, perhaps never fully getting there, but coming arbitrarily close. Such, at least, seems to be the hope.
That prior column ended with a discussion of the Kochen-Specker theorem, a famous result in the foundations of quantum mechanics that essentially entails that, when it comes to the (allegedly) microscopic realm subject to the laws of quantum physics, the above clear delineation is not possible in general. What we find must, to some extent, depend on how we look—the ontological inventory of the world is not independent from the epistemic process of interrogating it. Values of observable quantities, if they exist at all, must be contextual, that is, depend on what other values are queried simultaneously.
For the macroscopic world, this strikes us as an absurdity: the color of a ball, say, should not depend on whether it is simultaneously measured together with its size, or its weight! And in our everyday experience, where in principle all quantities can be observed simultaneously, no such effects occur. So perhaps this is just the quantum world being, you know, weird? Maybe for all practical purposes, we can still rely on the world being a solid bedrock of facts awaiting our discovery, like pill bugs hiding under so many rocks to be turned over?
In this column, I want to take a look at another quantum quandary, the Frauchiger-Renner paradox, named after its originators, ETH Zurich physicists Daniela Frauchiger and Renato Renner. Unlike the Kochen-Specker theorem, the observer—the scientist carrying out measurements and obtaining a given result—is an integral part of the setup. Indeed, according to Frauchiger and Renner’s original conclusion, their result intimates that quantum theory fails to consistently describe the use of quantum theory to describe the observer and their observations! Although, as we will see, there are other possible resolutions. But first, we need to avail ourselves of some basic notions of quantum mechanics, to get a little warmed up before tackling the argument head-on.
Quantum Preliminaries (And Preconceptions)
There is much philosophical discussion regarding what the ‘quantum state’ of a physical system actually is: does it describe physical ‘reality’ (there’s that word again!), or does it merely give some account of our knowledge, or is it something else entirely? Luckily, for us, that particular discussion won’t matter too much, so we’ll simply think about the quantum state as giving us a list of results we might see in a given experiment (together with the probabilities for those results, but even that won’t matter too much).
Moreover, we can concentrate on just a set of two measurements, which we’ll call the ‘vertical’ (↑↓) and the ‘horizontal’ (←→) measurement, with the possible outcomes {↑,↓} and {←,→}, respectively. (The quantum literate will recognize this as a simplified version of the phenomenon of quantum spin, as demonstrated in the classic experiment of Stern and Gerlach.)
Then, a quantum state, for us, will be just a list of possible outcomes, either for the ↑↓- or for the ←→-measurement. For instance, the list [↑,↓] just denotes a quantum system where, upon making the ↑↓-measurement, we might observe either the ↑ or ↓-outcome, while the list [→] tells us that upon making the ←→-measurement, we’ll definitely observe the outcome →.
So far, there is nothing quantum about any of this, at all. We have a system with two ways to interrogate it—two buttons to push, say—and a list of possible answers the system can give upon either button being pushed. Now, the ‘weirdness’ of the quantum world enters with the following claim: whenever a system is such that it always gives a single result for one of the two measurements, it can’t also give always the same result for the other. That is, a system in the state [→] must, with respect to the ↑↓-measurement, be in the state [↑,↓], and can’t be in, e.g., the state [↑]. In other words, with sufficiently many such systems, while we will obtain the result → every time we perform the ←→-measurement, upon measuring ↑↓, we will get either of ↑ or ↓ without any possibility to predict which. This is nothing but Heisenberg’s famous uncertainty relation, adapted for our toy example.
The above readily generalizes to ‘composite’ systems. For instance, a system in the state [↑↑,↓↓] will, if we perform an ↑↓-measurement on its components, always yield the same answer for each—although we can’t predict which one. A system in the state [←→] always yields the outcome ← for its first component, and the outcome → for the second.
With this mechanism, we can tackle our first warm-up case for working our way up to the FR-argument: the so-called Hardy paradox, named after British-Canadian theoretical physicist Lucien Hardy.
Hardy’s Paradox: Nonlocality Without Inequalities
In a previous column, I have tried to give a basic intuition for the phenomenon of ‘quantum nonlocality’ by means of the violation of so-called Bell inequalities. For all theories in which observable quantities have definite values that can’t influence one another instantaneously across arbitrary distances, it turns out one can derive bounds on the strength of possible correlations between observations. The violation of these bounds, then, indicates that quantum mechanics doesn’t fall into this class of theories.
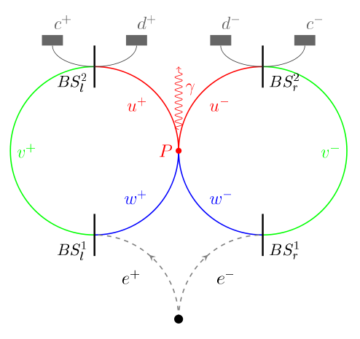
Hardy’s paradox is a way to arrive at a similar conclusion, using only reasoning about what quantum states allow us to conclude about possible observations. To this end, we start with a system composed of two elementary subsystems (a ‘bipartite’ system) in the state [↑↑,↑↓,↓↑]. That is, whenever we perform the ←→-measurement on both parts of the system, we can see either of the outcome pairs ↑↑, ↑↓, or ↓↑. Note that this means that the outcome of the measurement on one subsystem carries some information about the outcome on the other: if the first comes up ↓, the second must come up ↑, for example, as there is no ↓↓-component.
Using the rules of quantum mechanics, we can rewrite this state in terms of the ←→-measurement, which yields [←←,←→,→←,←←]—all possibilities (in particular, the possibility ←←) are open. This, we will now see, seems to lead to a contradiction.
Consider what happens if we perform the ↑↓-measurement on one, and the ←→-measurement on the other component. Again, using the rules of quantum mechanics, we can compute the state to be [↑←,↓→,↓→]. In particular, this tells us that obtaining the ↑-outcome on the first component means we must obtain the ←-outcome on the second.
Now consider what happens if we switch the measurements around, measuring ←→ on the first, and ↑↓ on the second. The state then is [←↑,←↓,→↓]. Hence, obtaining → for the first means we must obtain ↓ for the second. This now allows us to arrive at a contradiction.
- First, we know that → on the first implies ↓ on the second.
- But from the form of the state for the ↑↓-measurement on all components, [↑↑,↑↓,↓↑], we can conclude that ↓ on the second means ↑ on the first.
- Finally, ↑ on the first and [↑←,↓→,↓→] means ← on the second.
- Daisy-chaining the above reasoning together, → on the first implies ← on the second.
- But from the state in terms of the ←→-measurement on all of the components, [←←,←→,→←,←←], we know that the ←←-outcome must be possible: yielding the promised contradiction.
(Why is this considered a ‘nonlocality’-argument? In Hardy’s original setup, the measurements were realized by particles—an electron and its antiparticle, the positron—traveling through different paths in an interferometer. Where the particles are detected carries information about which path they have taken; in particular, a detection equivalent to our ←←-outcome indicates both taking the same path. But a particle and an antiparticle taking the same path should annihilate one another, leading to the conclusion that the ←←-outcome should be absent. Hence, they must interact somehow without their paths meeting—nonlocally, in other words.)
Now let’s take a look at the second ingredient to Frauchiger and Renner’s ingenious argument.
Wigner’s Paradox: Bring A Friend!
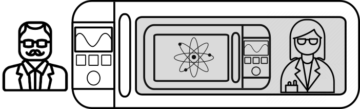
Erwin Schrödinger, father of the wave-function formulation of quantum mechanics, was greatly vexed by the implications of extending quantum mechanics to macroscopic objects, dreaming up the notorious case of a cat being both dead and alive as a way to voice his discomfort. Hungarian-American physicist Eugene Wigner took things a step further: rather than putting a cat in the box, he imagined an entire laboratory, complete with an experimenter, sufficiently isolated from the environment such as to make a probe of its internal state from the outside impossible.
Together with the experimenter—the eponymous ‘friend’—a single quantum system in the state [↑,↓] was present. Now, a tenet of quantum mechanics is that after an experiment has yielded an outcome, that outcome will be observed again upon repeating that experiment. Meaning that performing the ↑↓-measurement on a [↑,↓]-system and obtaining ↑, say, repeating the measurement must again yield the outcome ↑. Therefore, after the measurement, the system can’t be in the state [↑,↓] anymore, and must instead be in the state [↑]. This is the origin of the famous ‘collapse’ of the quantum state upon measurement: somehow, the state must make a transition from [↑,↓] to [↑] (or [↓]) when the ↑↓-measurement is performed.
Wigner now asked himself how quantum mechanics ought to describe the process of measurement itself, i.e. of an experimenter performing an experiment in such a way as to be subject to the usual rules of quantum mechanics (essentially, isolated from the environment sufficiently well to prevent decoherence). This involves modeling the experimenter themself using quantum mechanics. For our purposes, it will be enough to consider an experimenter with two possible states (for each measurement): [“↑”] or [“↓”] for ‘having observed ↑’ or ‘having observed ↓’, respectively (and analogously [“←”] and [“→”]).
Paradoxically, it seems that there are two answers: if the observation ‘collapses’ the state, then after making their measurement, the combined system consisting of the friend and the system they measure should be either described as [“↑”↑] or [“↓”↓], the object-system in a definite state, and the experimenter having definite knowledge of that state. But, modeling both as quantum systems, this is not what happens—rather, as with the dead-and-alive cat, we obtain a combined system in the state [“↑”↑,“↓”↓]—where neither the experimenter nor the object can be assigned any definite state.
Wigner thought this strange enough to postulate an absolute boundary for the quantum description at the experimenter’s conscious experience—it is this, he claimed, that causes the collapse (hence, the ‘Consciousness Causes Collapse’, CCC, interpretation). The quantum buck stops where the experimenter takes conscious account of a measurement result.
But this in itself causes complications. After all, in a physical world, an experimenter, even a conscious one, is just some configuration of particles—what should be special about that particular pattern? (More recently, an answer to this has been proposed, using tools from integrated information theory—essentially, postulating that the amount of integrated information, a measure for consciousness, that a state contains dictates its likelihood to spontaneously collapse.)
However, it makes the question—in principle, at least—amenable to experiment: whether the laboratory is in a state like [“↑”↑] or [“↑”↑, “↓”↓] can be revealed using a (fiendishly difficult, and in practice probably impossible) measurement on the combined system. A state like [“↑”↑, “↓”↓] can lead to interference effects, while a state like [“↑”↑] can’t—it is analogous to checking which path a photon takes in the classic double slit-experiment.
While the friend can carry out either the ↑↓ or the ←→-measurement, Wigner can thus perform experiments on the whole setup that essentially check whether the friend has observed a given outcome—which we will call the “↑↓” respectively “←→”-measurement, with outcomes {“↑”, “↓”} and {“←”, “→”}, respectively. (Note that we abbreviate, e.g., “↑”↑ by “↑”, and use it to indicate ‘the friend has observed ↑ and the system is in state [↑]’, because these always go together.)
We are now ready to combine the above ingredients into one big quantum pie.
Frauchiger-Renner: Applying Quantum Theory To Itself
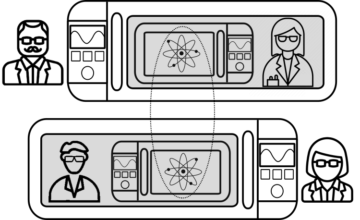
Frauchiger and Renner’s setup has been described as a ‘Wigner’s friendification of Hardy’s paradox’. And this is exactly how we will approach it. We start, again, with a quantum system in the state [↑↑,↑↓,↓↑], and two ‘friends’ carrying out ↑↓-measurements on both parts. Then we add the following twist: on each of the two (sufficiently isolated) laboratories, two ‘Wigners’ will carry out “←→”-measurements, that is, measurements checking whether the ‘friends’ have obtained the ←- or →-outcome. If a friend has measured ↑↓, and obtained, say, ↑, then with respect to the “←→”-measurement, they will be in an indefinite state—just as a quantum system in the [↑]-state is with respect to the ←→-measurement. In fact, performing the “←→”-measurement yields the same outcome possibilities as performing the ←→-measurement, with the crucial distinction that while you can’t simultaneously perform ↑↓- and ←→-measurements (because Heisenberg forbids it), you can perform a “←→”-measurement! That means the measurements we had to perform ‘virtually’ (or counterfactually) in the Hardy setup now can actually be implemented.
As before, then, we can write down the state for the “←→”-measurement as [“←” “←”, “←” “→”, “→” “←”, “←” “←”]. Note that the presence of the “←” “←”-outcome means that both friends could measure their part of the system and obtain the ←-outcome.
But now we reason as before.
- The state being [“←”↑, “←”↓, “→”↓] means that if the first Wigner obtains “→”, it implies that the second friend must obtain ↓ for their ↑↓-measurement.
- But from the form of the state for the ↑↓-measurement on all components, [↑↑,↑↓,↓↑], we can conclude that ↓ for the second friend means ↑ for the first.
- Finally, ↑ for the first friend and the state being [↑ “←”,↓ “←”,↓ “→”] means that the second Wigner must obtain the outcome “←”.
- Daisy-chaining the above reasoning together, the first Wigner obtaining “→” implies the second Wigner obtaining “←”.
- But from the state in terms of the “←→”-measurement on all of the components, [“←” “←”, “←” “→”, “→” “←”, “←” “←”], we know that the “←” “←”-outcome must be possible: yielding again a contradiction.
Consequently, it seems that if the first Wigner obtains the “←”-result, they can infer that the second Wigner must obtain the result “←”. But the result “←” “←” is evidently possible, too. What gives?
Frauchiger and Renner, as already noted, take their result to imply that quantum theory, when applied to observers themselves applying quantum theory, yields inconsistent results (so I guess, don’t do that). But this is not the only possible conclusion that can be drawn from this.
The fact that the above measurements can be actually carried out invites us to think of their results as ‘facts in the world’, i.e. that, for example, the first friend obtaining ↓ entails this to be a universal truth, and allows them to conclude that the second friend must find ↑. That is, the result is paradoxical only as long as we assume the picture of the world as a bedrock of objective facts, where our only role is that of the distant observer. By now, I hope this strikes you as questionable, at least.
From this point of view, what the Frauchiger-Renner Gedankenexperiment really tells us is the impossibility of observer-independent facts, or the impossibility of a fully objective world independent of any subject within. There is not only a single story that can be told about the world; rather, there exists an inevitable patchwork of stories that can’t be unified into a single, coherent whole. As in Kurosawa’s classic Rashōmon, truth is not a monolithic entity, but instead a multifaceted concept reflecting, to some extent, always the faces of those trying to peer into it.
Perhaps, then, terms like ‘reality’ indeed do not pick out any singular concept, but instead, serve just as a placeholder for a far richer tapestry of stories weaving around each other without ever quite fully joining together. And perhaps, rather than just being a passive, detached observer, each of us is responsible for spinning our own yarn.
