by Jochen Szangolies

Sunil Rao, one half of the leading duo of the novel Prophet by Helen Macdonald and Sin Blanché, has a gift: he can tell trick from truth. Any fake is immediately obvious to him; any false statement revealed as such upon hearing it. Much more than a human lie detector, his abilities are not dependent on whether those making the statements—or indeed, anybody—know the truth: indeed, on occasion, he engages in accidental self-discovery, by uttering statements about himself and finding them true.
Rao, then, seems ideally suited to his secret service work, but, without giving away too much, things are more complicated than that. Nevertheless, somebody with his ability might seem to be an asset to have in your corner, in this age where simple truth seems under attack from multiple sides. Who wouldn’t want to read the news and just know what’s what? Know whether the latest fad diet delivers on its promise (although I’d venture a semi-educated guess there)? Perhaps even have a shot at the Big Questions™—God, life, the universe, and all that?
Indeed, to a scientist, philosopher, or any such habitual question-asker, perhaps nothing ought to seem more tantalizing than a direct mainline to truth. Mathematical physicist Geoffrey Dixon shows his literary sensibility when he begins his monograph Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics with a series of brief ‘Screeds’ concerning a visitation by the Screen of Ultimate Truth, ready and waiting to spill the universe’s (mathematical, presumably) guts upon being prompted.
But what question to pose? Suppose you ask, as the physicist in Dixon’s Screed does, for the ultimate reason for the universe’s existence, only to be met with pages upon pages of incomprehensible symbols: what good is truth you don’t have the proper context for?

During the main plot of Prophet, I frequently became distracted by what the mere existence of Rao’s ability intimates about the universe. The mere possibility of such a direct line to truth implies a certain bedrock of solid fact upon which the edifice of the world is erected. Fix those facts, and everything else will follow just as inevitably. Gain access to them, and the secrets of the world are laid bare.
I don’t think that’s at all how it works. Moreover, in a sense, such a world would be fundamentally unintelligible: suppose you’re handed, whether by the Screen or through Rao’s judgments, the full set of those facts—then what? Everything you know, you’re certain, can be derived, by application of sufficient reason, from that set of ground truths. Why the sky is blue, how (fucking) magnets work, why your first love left you, why bad things happen to good people: these all will find their final justification with that basic set of facts. But then, what justifies them? If nothing, then why are they true? If there is a further justification, in terms of what further facts (or turtles?) is that formulated?
Atoms Of Thought
The existence of fundamental truth from which everything else follows is the view of logical atomism. Somewhere at the (very deep, presumably) bottom of every true statement, there is a set of ultimate facts that can’t be analyzed further. Bertrand Russell is often cited as one of its founding fathers, although, as with so many things in Western philosophy, an argument might be made that the ultimate logical atom from which every certainty is supposed to flow is Descartes’ Cogito. Russell’s pupil Wittgenstein (in his early incarnation) endorsed this view when he considered the world to be ‘the totality of facts’. Rudolf Carnap tried to find a ‘constitution theory’ from which the world is derived in Der Logische Aufbau der Welt (The Logical Structure of the World), a project that was, to some extent, taken up in more modern times by David Chalmers (him of the ‘hard problem’) in Constructing the World.
Chalmers central notion is that of scrutability: roughly, what could be concluded from a certain set of fundamental truths, the scrutability base, by an ideal reasoner. To make this more vivid, he introduces a particular device, the Cosmoscope, which is able to store the entire scrutability base, and, by means of vast amounts of computation, create a sort of virtual reality simulation of the world given the base. In this, the Cosmoscope is a relative to both Dixon’s Screen of Ultimate Truth and Rao’s ability to tell fact from fiction.
Chalmers also presents a candidate for a scrutability base—the set PQTI, where:
- P represents the base set of physical truths (laws, initial conditions, physical entities, and the like)
- Q represents basic phenomenal or experiential (‘qualitative’) facts, such as what it is like to be a certain entity having a certain experience at a certain point in time
- I is the set of indexical facts, that is, facts of the form ‘I am Jochen Szangolies’ or ‘it is now 18:57’
- T is just a single, ‘that’s all’-fact, that states that there is nothing beyond the above; this is needed to derive negative statements, like ‘there is no extraphysical ectoplasm’

The precise makeup of the scrutability base is, of course, subject to debate—a Platonist might want to add mathematical truths M, a moral realist ethical facts E; a physicalist might want to get rid of Q (and perhaps of I, as well—though see here for some reasons why that might not be such a good idea).
At any rate, given the right scrutability base, the Cosmoscope will (re-)produce every true fact of the world, and, we may presume, present it to you in 4K quality 3D rendering. However, the convenience of its user interface hides too much of its inner workings—it presents you with a seductive contact surface that fosters an illusion of immediacy: ask, and ye shall receive. To make vivid the troublesome notions behind the sleek presentation, it is more instructive to consider Rao’s somewhat less user-friendly ability.
While he can tell true from false statements, Rao can’t tap into the scrutability base itself and conjure up any given fact from it. Where the Cosmoscope can answer arbitrary questions, Rao can answer decision problems: for each statement, you obtain one bit of information, depending on whether it is true or false.
This might, at first, seem to be a considerable hindrance. But every problem can be repackaged as a decision problem (or a set of decision problems): rather than asking for the answer to any given question, we can just test whether a candidate answer is the right one. Rao employs his abilities to this effect at several points in the book, doing what he calls a ‘truth run’, for instance figuring out the name of an official by running through the alphabet sequentially. In general, this is going to take a lot of time, but we’ll imagine we’re not in a hurry.
Each of the three—Sunil Rao, the Screen of Ultimate Truth, and the Cosmoscope—seem to be able to divulge every truth, provided time is not an issue. Sadly, we don’t have access to either! But even their mere possibility tells us quite a bit about the world in which they exist. In fact, even though they seem, at first glance, to be of equal power, there are large gaps between them, and in turn, a marked difference in the scrutability base of each of these worlds.
Levels Of Scrutability
In Rao’s world, the scrutability base is such as to allow that for every statement, it is decidable whether it follows from it. The set of facts about this world, we may say, is ‘fully scrutable’. The Screen, on the other hand, only produces true facts—every true fact, we may suppose, eventually. It can enumerate all the facts that follow from the scrutability base in its world; hence, let’s call the corresponding set of facts ‘scrutably enumerable’.
The Cosmoscope, thanks to the ‘that’s all’-truth T, has powers exceeding either of these: it can enumerate negative facts, as well. It can fully ‘scrute’ a set that’s only scrutably enumerable by ‘conventional’ means.
This might seem an arbitrary classification, at first. But it trades on an analogy with computability theory. There are certain sets that are computable: any computer (given enough memory and time) can decide, for any given object, whether it is in that set. The set of prime numbers is an example: whether a number is prime can be easily decided by successively attempting to find divisors (although of course more efficient algorithms exist). A fully scrutable world is then one in which, for each statement, there is some test to see whether it is true.
But there are sets that are not computable, such as, for example, the set of all programs that halt for a given input. Any halting program can eventually be identified: just run it until it stops. But because of the undecidability of the halting problem, there is no general procedure that identifies programs that don’t halt. The best one can do is to fix a particular ordering of programs, and then tell a computer to simulate all possible programs step by step. (Again, we’re not in a hurry.) Whenever a program halts, we add it to the list.

This procedure will eventually produce every halting program, but for non-halting programs, we’ll never know if they actually fail to halt, or if we just haven’t waited long enough yet. Such sets are called ‘computably enumerable’, because there exists a way to list all members successively. By analogy, a world all of whose truths are eventually producible is one with a ‘scrutably enumerable’ base: every true statement will eventually be produced, but not any given statement can be decided.
However, we can try to overcome this limitation. For instance, we could augment our computer with a device that, magically, is able to decide whether any given program halts. Such a device, usually called an oracle, would enable a computer to go beyond the usual limits of computation—it would make it into a hypercomputer.
The ‘that’s all’-truth T in Chalmer’s scrutability base effectively functions as such an oracle. Having access to it, the Cosmoscope can scrute the inscrutable: it cannot merely find every consequence of the facts in the scrutability base, but also determine what can not be produced from it.
We thus have a two-dimensional characterization of possible worlds: we can classify them according to the nature of their scrutability base, as well as according to the powers of scrutability possible within them. The ‘simplest’ kind of world is one with a fully scrutable base, needing only ordinary scrutability to discover the truth or falsity of any statement. In a world with a scrutably enumerable base, these same powers then only serve to (eventually) produce every true statement, with false statements generally remaining open. Adding ‘hyperscrutable’ power to this world, we then can again discover the truth or falsity of any given statement.
These two axes correspond to the two fundamental disciplines of metaphysics: the study of the nature of what exists in the world (ontology), and the study of what we can know about it (epistemology). These seem to be entirely orthogonal: there is some set of true facts about the world, which can either be known, or not. But as we’ll see shortly, whether this really is the case is dubious.
But first, a small digression. Our three worlds above seem to exhaust the possibilities, but there is a good reason to think that we can further iterate the classification. Adding an oracle to an ordinary computer allows it to decide the halting problem for any ordinary computer; but it can’t solve that problem for computers like itself, that are enhanced by oracular means. Translated to our setting, this would mean that there are certain questions about the scrutability powers of the Cosmoscope that it can’t answer itself. I have not attempted to find a formal proof of this, but the Austrian physicist Karl Svozil proves a related proposition in his monograph Randomness and Undecidability in Physics, showing that in general, no apparatus can obtain a full theory of its own functioning by means of self-introspection.
If this is right, then, we have a hierarchy of degrees of scrutability: a 1-Cosmoscope can scrute facts inscrutable to any ‘ordinary’, Rao-like scruter, a 2-Cosmoscope can scrute facts pertaining to a 1-Cosmoscops that are inscrutable to itself, and so on—we never reach an end-point where everything is scrutable.
Scrutability In Context
The idea of a scrutable world, with powers of scrutability being separate from the nature of the scrutability base, lies arguably at the heart of modern science—the world is cleanly divided into subjective and objective aspects, and the subjective can be abstracted away in order for an objective description of the real world to remain. Our means of knowledge acquisition (epistemology) don’t impact on the facts of the world (ontology), except regarding their knowability.
This picture of facts existing independently of their means of discovery finds its most elementary expression in George Boole’s Laws of Thought, which formulated what is now known as Boolean algebra—a logical calculus for combining statements and drawing conclusions in a truth-preserving way.
Boole’s algebra is the tool that, with some more modern elaborations, underlies the thesis of logical atomism: starting with the atoms, it allows to derive any logical consequence. In this atomistic world, and the entire hierarchy of scrutable worlds considered above, facts are absolute: any given statement is either true or false, independently of whether we can know it to be so, and of the methods we might use to ascertain its truth.
From this starting point, Boole was able, in a later publication, to derive certain conditions on the relative frequencies (i.e., probabilities) of observed events that must be fulfilled. These ‘conditions of possible experience’, are today better known as Bell inequalities, after their rediscovery by Irish physicist John Stewart Bell roughly 100 years later. (Previous column on the topic.) The fact that they’re violated in the actual world means that Boole’s assumptions in their derivation don’t hold—and, as I will argue presently, on one natural reading that the thesis of logical atomism and free-standing facts independent from their means of discovery fails to hold.
The argument can be made somewhat more neatly by appealing not to Bell’s work, but to a theorem by the mathematicians Simon Kochen and Ernst Specker. The Kochen-Specker theorem pertains to exactly the question of whether it is generally possible to assign fixed truth values to propositions. The original proof is a tour-de-force, utilizing 117 spatial directions along which the (squared) spin of a spin-1 particle (a photon or suitable atom) is measured. The outcome of these measurements can be either 1 or 0, with the constraint that for three orthogonal directions, two will be 1 and one 0. Kochen and Specker now find that for the directions in their proof, no consistent assignment of ones and zeros to all directions obeying this constraint is possible: we can’t think of these propositions as having fixed, pre-determined truth values.
Nowadays, far simpler proofs exist. The one due to N. David Mermin and Asher Peres takes the form of a square of nine measurements, where the measurements in each row and column can be performed together (recall that in quantum mechanics, not all measurements can, due to the uncertainty principle):
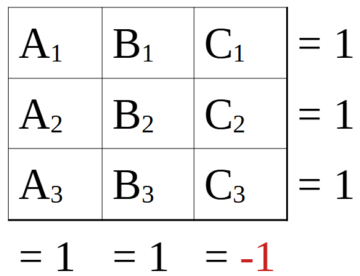
Each measurement can yield the value 1 or -1, and the rules of quantum mechanics allow us to derive that the value of the product of the outcomes of the measurements in every row, and in the first two columns, is equal to 1, while the product of the values of the last column must always be -1. Now, the challenge is to assign values of 1 and -1 to the individual measurements. You’ll quickly find that you can’t do it: there is no assignment that satisfies the constraints.
What does this mean? It means that we can’t assign a fixed value to, say, A1 in isolation; we must always consider it together with either A2 and A3 or with B1 and C1—we must always consider its context. Facts in quantum mechanics are not independent of their means of discovery: the epistemic and ontic axes are not orthogonal. Whether we want to scrute A1 together with A2 and A3 or together with B1 and C1makes a difference for its value.
The quantum world does not fit into our characterization of scrutable worlds.
To be sure, there are ways to avoid this conclusion. For instance, there could be fixed values to each quantity, a fixed scrutability background, but measurements lead to unavoidable changes to these facts—this is the way out taken by the Bohmian interpretation of quantum mechanics. However, ultimately, these strike me as rather evasive: a better way forward, I believe, is to go back to basics and reevaluate our assumptions regarding the existence of independent and independently knowable facts, of a clean separation between ontology and epistemology, objectivity and subjectivity.
