by Jochen Szangolies

The previous column left us with the tantalizing possibility of connecting Gödelian undecidability to quantum mechanical indeterminacy. At this point, however, we need to step back a little.
Gödel’s result inhabits the rarefied realm of mathematical logic, with its crisply stated axioms and crystalline, immutable truths. It is not at all clear whether it should have any counterpart in the world of physics, where ultimately, experiment trumps pure reason.
However, there is a broad correspondence between physical and mathematical systems: in each case, we start with some information—the axioms or the initial state—apply a certain transformation—drawing inferences or evolving the system in time—and end up with new information—the theorem to be proved, or the system’s final state. An analogy to undecidability then would be an endpoint that can’t be reached—a theorem that can’t be proven, or a cat whose fate remains uncertain.
Perhaps this way of putting it looks familiar: there is another class of systems that obeys this general structure, and which were indeed the first point of contact of undecidability with the real world—namely, computers. A computer takes initial data (an input), performs a transformation (executes a program), and produces a result (the output). Moreover, computers are physical devices: concrete machines carrying out computations. And as it turns out, there exists questions about these devices that are undecidable.
That this is the case was shown just a few years after Gödel’s landmark result, in 1936, by the British mathematician Alan Turing—who, besides essentially inventing the modern computer, was also instrumental in cracking the code of the German ‘Enigma’, thus speeding up the war effort and likely saving millions of lives. Tragically, he died of cyanide poisoning in 1954, possibly self-administered, after having been convicted of homosexual acts and undergone chemical castration the year before. He was 41 years old.
The problem Turing had set his sights on in 1936 was one posed in the prior decade by, again, David Hilbert as a part of his program: given a well-defined mathematical statement, is there always a way to mechanically—by means of ‘effective calculation’, the step-by-step execution of certain logical rules—decide whether it is valid? Turing showed that the answer to this Entscheidungsproblem (‘decision problem’) was negative, by exhibiting a statement such that there is no general way (that is, one applicable for every case) to decide, by rote symbolic manipulation, whether it holds.

To do so, Turing first had to find a way to precisely formulate intuitive notions such as ‘mechanical’, ‘effective calculation’, or ‘rote symbolic manipulation’. His solution was to design a hypothetical machine, the ‘A-Machine’, consisting of an (infinite) tape, a set of symbols, a read/write head to manipulate these symbols, and a set of rules to do this rewriting. In doing so, Turing came up with the first formal definition of the modern-day computer, today called ‘Turing Machine’ (TM) in his honor.
A TM is intended to be an abstraction of a human mathematician. Starting out with a string of symbols, a mathematician uses fixed logical rules to re-write those symbols, until they arrive at a desired form—signifying the completion of a calculation, or the proof of a theorem. The question Turing now asked, was: can we always tell whether that process eventually succeeds? That is, given an arbitrary set of symbols as ‘input’, does a given TM eventually enter a special ‘halting’ state signaling completion?
Turing found that he could bring this halting problem into a form a TM would understand: each such machine A can be unambiguously described by some set of symbols detailing its actions on encountering specific symbols, and thus, serve as input for another machine B. That machine, in turn, could then be given an input for A, A’s description, and the task of determining whether A ever enters the halting state.
But Turing showed that this task was impossible: there is no B such that it could determine, for every A, whether it halts. The question is undecidable. The analogy to Gödel’s result is immediate—in fact, if one requires that the theory under discussion only proves true theorems, Gödel’s theorem can be immediately obtained via Turing’s formulation.
The remarkable difference in this case, however, is that Turing’s proof is not confined to a pristine, but abstract, mathematical realm: it makes a claim about a putative physical system, namely, that whether that system (the TM) ever reaches a certain state (the halting state) is undecidable.
(There is a caveat, here: a TM’s tape is infinite, or at least unbounded; indeed, putting an upper bound on its length makes the halting problem for this class of machines decidable—by a bigger machine. If concretely realizable systems are always finite, one might thus hold that TMs aren’t physically realizable, but merely abstract objects, after all. However, while systems with infinite tapes are difficult to envision, there are systems with infinitely many degrees of freedom in a sense that bridges this gap: as shown by Toby Cubitt from London’s University College and collaborators, for quantum many-body systems, whether there is a finite difference in energy between the ground state and the first excited state is just such an undecidable problem.)
Thus, there are real-world consequences to undecidability—real questions concerning physical systems we can ask, but cannot formally answer.
A Universal Consequence
Given the above, we might well ask: under what circumstances do the phenomena of undecidability manifest? What is required for the existence of undecidable questions?

A putative reason is often given: what invites the allegedly ‘paradoxical’ consequences of undecidability is claimed to be the notion of self-reference, the ability to bring statements about a system back under the purview of the system. Thus, it was Gödel’s encoding of the ‘liar paradox’, the self-inconsistent statement ‘this statement is false’, into a mathematically tractable form—essentially, a sentence that asserts that a sentence constructed in a particular way is unprovable in a given system, which turns out to be that sentence itself—that tore an unpatchable hole into the foundations of mathematics.
While there is merit to that notion, it is ultimately too limited. Certainly, there is an element of self-refutation in both Gödel’s and Turing’s constructions: whenever one tries to assign a particular truth value to a statement, it seems to reach back into itself and flip the switch to become its own negation. But many undecidable statements are not self-referential, and there exist similar constructions that do not overtly involve self-reference. One example is Yablo’s paradox, which consists of an infinite family of sentences, each of which cannot be consistently assigned a truth value, without referring back to itself.
But both Turing’s and Gödel’s results share a similarity in the way their theories seem to extend their scope beyond the originally intended domains. Gödel found that he could encode arbitrary number-theoretical statements into numbers; Turing found that his ‘A-Machines’ were themselves objects of the theory of computation he intended them to represent. For Turing Machines, this property is called universality: they are themselves objects of their own ‘universe’—like the dreamer inhabiting their own dream. It is this property that enables the success of modern computers: whatever their design, they can all perform the same computations—if need be, by explicit simulation, running, say, a virtual Windows machine on a Mac.
If we leave this universe, we also break free of the paradox: suppose we have access to an ‘oracle’ that can tell us whether a given program halts. Giving a TM access to this oracle, we obtain what Turing called an ‘O-Machine’. As this now can perform computations that no TM can perform, it is no longer a member of their universe, but inhabits some separated realm. As long as it only takes TMs as its object, no paradoxical consequences ensue.
But now suppose we ‘enlarge’ the universe to include O-Machines, and ask for a solution to their halting problem: again, we find the same old troubles resurface, and undecidability return once more—the O-Machine halting problem is undecidable for O-Machines.
Thus, undecidability seems to emerge whenever a theory’s substrate—the axioms of number theory, Turing’s A- and O-Machines—becomes the theory’s own object. The analogy to physics is immediate. Many theories are such that they apply to a limited set of phenomena. Maxwell’s theory of electromagnetism describes phenomena concerning the behavior of charges in electric and magnetic fields—a comprehensive, but clearly delineated subset of the (physical) universe. These can be studied ‘from the outside’: the theory has a limited scope.
But any putatively fundamental theory, claimed to apply to literally everything in the universe, leaves no ‘outside’ from which its phenomena can be appraised—it leaves no room for a ‘detached observer’: any possible observer must themselves be an object of the theory. Thus, once a physical theory is universal in this sense, we are in a situation much like that of Gödel and Turing. It is then only natural to look for analogous consequences, as well.
This circumstance has been noticed several times in modern physics. One of the earliest examples, in fact, is due to philosopher Karl Popper, originator of the falsificationist approach to the philosophy of science. In 1950, Popper, in a two-part paper entitled Indeterminism in Quantum Physics and in Classical Physics, considers ‘near-Gödelian questions’, and proposes that they imply ‘the physical impossibility of predicting […] certain physical events; or […] an indeterminism of a kind somewhat similar to the one implied by quantum physics’.
However, the task Popper has in mind really is that of self-prediction: asking an agent about their future state. Important work along related lines was done by the eminent quantum logician Maria Luisa Dalla Chiara, who in 1977 explicitly considered the famous ‘measurement problem’ of quantum mechanics in light of the Gödelian results, by the Austrian mathematician Thomas Breuer, and the Viennese physicist Karl Svozil.
These results largely concern Gödelian phenomena as applied to quantum theory. Wheeler’s intuition, however, was quite different: that undecidability might be a foundational principle of quantum theory. That, in other words, quantum theory is quantum because of undecidability. This is a more daring possibility: if it is correct, then it would imply that classical physics was never an option—that the impossibility of predicting certain outcomes is, in fact, a necessary feature of any putatively ‘universal’ theory.
Here, an early proposal is due to Martin Zwick, now professor emeritus of systems science at Portland State University, who in 1978 argued that the state of a system after a (quantum) measurement is analogous to a proposition undecidable from the axioms of a mathematical theory. Along similar lines, the point is made more forcefully by Asher Peres, one of the founding figures of quantum information theory, and Wojciech Zurek, an originator of the influential decoherence-program in quantum theory. In a 1982 article, they claim that quantum theory’s ‘inability to completely describe the measurement process appears to be not a flaw of the theory but a logical necessity which is analogous to Gödel’s undecidability theorem’—thus explicitly referring to the foundational significance of undecidability.
Yet, these perspectives have, for the most part, remained scattered and isolated, localized flare-ups that failed to ignite large-scale fires. However, in recent years, perhaps this has begun to change. Take the latest installment of the essay contest organized by the Foundational Questions Institute (FQXi) on the topic of ‘Undecidability, Uncomputability, and Unpredictability’. Several of the ten prize-winning essays, collected and expanded upon in the accompanying volume, investigate the question of the relevance of undecidability for quantum mechanics (among them the author’s humble contribution). Maybe now the time is right for Wheeler’s ‘idea for an idea’.
Algorithmic Undecidability: A Die-Roll in Pure Maths
There is still a gap to bridge between the relevance of undecidability to the foundations of quantum mechanics and the principles of finiteness and inexhaustibility as proposed before. After all, the inability to answer every question about a system does not entail that only finitely many questions can be answered!
The connection is made by means of the results of Argentine-American mathematician Gregory Chaitin, one of the main architects of the field of algorithmic information theory. The central object of this theory is the eponymous algorithmic information—also known as Kolmogorov complexity, after Russian mathematician and founder of modern-day probability theory Andrey Kolmogorov. Loosely speaking, the amount of algorithmic information contained in an object is the shortest possible description needed for a computer to reproduce it. So, for something highly regular, like a sequence containing only the number 1 ten billion times, a short description (like ‘the number 1 ten billion times’) is sufficient, while a sequence with ten billion random digits will typically have to be written out in full—signaling a much higher algorithmic information content.
This already hints at an important result: random sequences have maximal algorithmic information content. In fact, this is so fundamental as to be a useful definition of randomness: a sequence is (algorithmically) random if it cannot be compressed—if we can find no significantly shortened description causing a computer to reproduce the sequence.
Moreover, it establishes a direct line from mathematical undecidability to randomness. Indeed, for infinite random sequences, it turns out that only the values of finitely many digits can be decided—thus making each further digit an undecidable proposition! Translated into the physical realm, this finally yields the principle of finiteness.
Returning to the arc traced by TWA 702 between New York and London, at any given instant, only a finite amount of information is available to describe its state—its precise location and speed must thus be subject to an irreducible uncertainty, and its future course ever so slightly indeterminate. If sufficiently amplified, this uncertainty then might make questions about its future state—whether it is rocked by a patch of turbulence, say—just as undecidable as the state of the cat in the box.
Randomness, of course, lies likewise at the heart of quantum theory—and Einstein’s disagreement with it. Einstein, whose explanation of the photoelectric effect using Max Planck’s hypothesis of energy quantization had been seminal to quantum mechanics (and won him the Nobel prize), would famously later go on to claim that ‘God does not play dice with the universe’, and search for a deterministic ‘completion’ of the theory. It might be considered a certain kind of (to Einstein, no doubt, bitter) historic irony if such completion should be impossible in the same sense Einstein’s close friend Gödel had already shown that of mathematics unattainable.
What Lies Beyond the Epistemic Horizon
Quantum mechanics, today, is widely viewed as a theory whose mysteries have resisted unambiguous solution since its inception, nearly a century ago. One might argue that little is gained by deferring their answers to the impossibility of deciding the undecidable: far from yielding any resolution, it tells us that we should not hope for it in the first place—none is forthcoming.
But that is too limitative a view on these results. Gödel’s proof is often portrayed as uncovering a ‘flaw at the heart of mathematics’, a defect or gap frustrating the search for truth; but this takes the perspective of the mathematician as defining the nature of mathematics, as such. Because ultimately, the ‘flaw’ lies not with mathematics, but with our theories of mathematics. Gödel tells us that we can find no theory that spits out every truth about the natural numbers in an orderly manner; but there is no reason that the natural numbers themselves should be bothered by this in the least. They are not what is indeterminate (in so far as they can be said to exist as independent objects)—the limits are merely on our theories, our abilities to build models of them.
The same, then, would be true of physics. All of our theories, all of our models, would necessarily fall short of physical reality—the latter being, in a sense, too rich, too vast in scope, to be encompassed within a singular theoretical framework. It is then just a matter of human hubris to project our limitations concerning the models we can build of nature into nature.
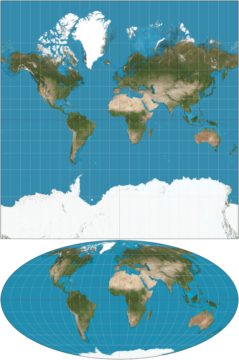
Models and their object—what they are a model of—can never be in perfect congruence: this is then the true impact of results of the Gödelian type. Any theory of the natural numbers must always fall short, and so must any theory of the world. It is neither a failure of mathematics, nor of the world: but an unavoidable property of model-building. This is not such an unusual circumstance. Consider map-making: a Mercator-projection of the globe will contain perfect angular information, while a Mollweide-projection faithfully represents areas. No simultaneous map perfectly representing all aspects of the Earth is possible—but that fact ultimately tells us more about map-making than the Earth.
We are now back with Wheeler on TWA 702, as the clouds below burst open and reveal the coastal outline of Great Britain: from this elevated position, he can see more than any observer on the ground, his horizon wider than is possible from the surface. But of course, no matter the altitude, no horizon can ever be so wide as to encompass the whole world. It is not the world that is at fault, here; this is just an unavoidable consequence of the relation between it and the observer. We only ever see a finite part of it, and no perspective can fully exhaust its manifold phenomena. But we do not therefore conclude that the world ends at the boundaries of our horizon.
Likewise, the limitations placed upon our theories by results of a Gödelian nature provide an ‘epistemic horizon’, a horizon of our knowledge, regarding any physical system. This horizon is captured in the principle of finiteness above: there is a boundary to the information available regarding any physical system. That the system is not exhausted by this knowledge yields the principle of inexhaustibility.
Taken together, then, many of the puzzling phenomena of quantum mechanics are just expressions of our inability to capture the world, in toto, within the confines of a single model. Novel phenomena emerge, like ships appearing over the horizon, first mast and sail, then bow and hull, unpredictable from anything observable within our purview.
To be sure, the impossibility of total knowledge might seem something to lament. But there is a lesson of humility in this, and in accepting it, there lies a certain kind of grace: human knowledge must remain always flawed, always incomplete—but in that, also ever growing, ever evolving. The static view from nowhere is not for us to be attained. Total knowledge of the world carries the price of being separated from it by an unbridgeable chasm.
I, for one, prefer the excitement and uncertainty of right now, right here.
