by Jochen Szangolies
TWA Flight 702 left New York at 7 AM on Monday, Feb. 4 1974, to arrive in London at 7 PM—some 40 minutes early. We know this thanks to the meticulous note-taking habits of visionary physicist John Archibald Wheeler, coiner of such colorful terms as ‘quantum foam’, ‘wormhole’, ‘superspace’ and ‘black hole’.
Wheeler spent the flight occupied with what he is perhaps best remembered for: pondering his ‘Really Big Questions’ (RBQs), among which we find perennial mysteries such as ‘How come existence?’ or ‘What makes meaning?’. The RBQ that occupied Wheeler on this particular day, however, was one that in many ways lay at the nexus of his thought: ‘Why the quantum?’
Wheeler had been a student of Bohr and Einstein, and thus, had learned about quantum mechanics straight from the horse’s mouth. Yet, he would struggle with the implications of the theory for the rest of his life, referring to the fundamental indefiniteness of its phenomena as the ‘great smoky dragon’. He was searching for a way to dispel the smoke, and in the note composed on Flight 702, draws a surprising connection to another remote frontier of human understanding—the phenomenon of mathematical undecidability, as discovered in 1931 by the then-25 year old logician Kurt Gödel. (The note itself is available online at the John Archibald Wheeler Archive curated by Baruch Garcia.)
At first sight, one might suppose this connection to be little more than a kind of ‘parsimony of mystery’: in substituting one riddle for another, the total number of unknowns is reduced. Indeed, the idea of ripping Gödel’s result from the austere domain of mathematical logic and injecting it into physical theory is controversial—earlier, during the writing of his magisterial textbook on General Relativity, Gravitation, with Charles Misner and Kip Thorne, Wheeler had confronted Gödel himself with the idea, who did not react too enthusiastically.
In fact, some sources claim that Wheeler was ‘thrown out of Gödel’s office’, but according to the way the story is told in Jeremy Bernstein’s Quantum Profiles, he merely changed the subject. There, it is also relayed that Wheeler would learn the reason for Gödel’s dismissiveness a year later: apparently, Gödel had become skeptical of quantum mechanics thanks to the influence of his close friend, Albert Einstein. But evidently, Gödel could not quell Wheeler’s ‘idea for an idea’ regarding the origin of quantum weirdness; and others, both before and after Wheeler, have felt the same strange pull.
But what is the source of this attraction? How does the Gödelian result dissipate the smoke that cloaks the dragon’s form? The story is best understood by thinking about quantum mechanics not in terms of how to interpret it, as is usually done, but rather, trying to find a way to reconstruct it from the ground up—searching for what Wheeler termed the ‘quantum principle’, the underlying key idea illuminating the mystery of the quantum.
The Problem of Quantum Mechanics
The problem of quantum mechanics is typically phrased in terms of interpretation: we have been given—whether by divine providence or diabolic mischief—this theory, that describes the results of our experiments with unprecedented precision; now, what does it tell us about the world? However, where science is usually a story of unification—the electric and magnetic phenomena being unified in Maxwell’s theory; the behavior of elementary particles subsumed in the Standard Model—there has been little in the way of convergence regarding the interpretation of quantum mechanics. To the contrary, new interpretations seem to branch off at an alarming rate, much like parallel worlds are proposed to do in one of the leading contenders, the many-worlds interpretation by Wheeler’s student Hugh Everett III. Showcasing this embarrassment of riches, the wikipedia article currently lists 15 different ‘influential’ interpretations of quantum mechanics, and many more ‘minority’ approaches persist.
Perhaps, then, a different approach to the problem of quantum mechanics is called for. Sometimes, the converse of a difficult problem is easier to handle. While finding the prime factor decomposition of a large enough number is hard enough that we wager the whole of modern cybersecurity on its practical insolubility, multiplying numbers together is all but trivial (the downside being that you don’t know what you’ll end up with until you’ve tried). Hence, rather than taking the theory and using it to guess at the world beyond, we might start with the characteristics of a possible world, and see what theory emerges from them, in the hopes of zeroing in on quantum mechanics.
The prime exemplar of a theory formulated in these therms is Einstein’s special theory of relativity. Its physical content can be encapsulated in two short and readily appreciable statements about the world it describes:
- The laws of physics are the same in all inertial frames of reference (that is, those not subject to acceleration).
- The speed of light in vacuum is the same for all observers.
Any question that arises within special relativity can ultimately be traced back to these two principles. Hence, if we were to ask why the clock of a system in motion relative to us ticks slower than our own, the answer would be, because the laws of physics are the same in all inertial frames of reference, and the speed of light in vacuum is the same for all observers. Granted: this answer does take some unpacking. But in the end, we know we can always get there.
Such principles are lacking for quantum mechanics. To be sure, the theory can be formulated in terms of a certain list of statements that define it uniquely—usually around six. But these are generally formulated along the lines of, ‘a quantum state is a unit vector in Hilbert space’, which I think most will agree lacks the flair of the principles of relativity.
In contrast to the quest for interpretation, the project of reconstruction has produced some significant consensus. As pointed out by CEA-Saclay researcher Alexei Grinbaum, two principles, perhaps first made explicit by Carlo Rovelli, a founder of Loop Quantum Gravity, are common to several information-theoretic reconstruction approaches. For short, I will refer to these as ‘finiteness’ and ‘inexhaustibility’:
- Finiteness: There is a finite maximum of information that can be obtained about any given system.
- Inexhaustibility: It is always possible to acquire new information about any system.
There is an obvious tension between these statements: if there is a finite maximum to the information available about a system, once we have saturated that amount, how could it be the case that there is additional information obtainable? The answer is simple, yet contains the key to several of the puzzling features of quantum mechanics: upon acquiring new data, old information about the system must become ‘invalidated’, in some sense. It’s best to approach this idea by means of a simple example.
Getting Quantum Mechanics off the Ground
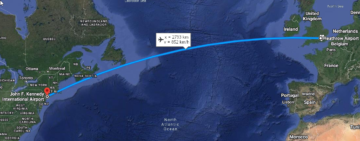
Let us return to Wheeler on TWA 702. Its journey from New York to London can be completely characterized by two numbers: the distance it has traveled (i. e. its position on the flight path), and the speed at which it is going. Consequently, the state of the airplane can be represented as a point on a two-dimensional plane, such that (say) the x-axis tells you where it is, and the y-axis how fast it’s going.
Suppose, now, you don’t have perfect information about the plane’s position. Then, rather than a point, there will be some interval within which it might be located—say, somewhere between kilometers 2750 and 2850 on its roughly 5700 km trip. You could now increase your information about the plane’s position by measuring whether it is in some particular location—that is, by going there and looking up; fortunately, plane positions are not very hard to measure. If you see the plane, say, at km 2793, you will have perfect knowledge of the plane’s position.
Let’s make things a little harder. Say that the sky, on that particular Monday in 1974, was cloudy, and thus, you can’t see the plane from the ground. Still, you might be able to hear it. This won’t give you perfect information about its position: all you know is that it must be somewhere within earshot—let’s call that a 5 km radius for simplicity. Thus, you might now be able to locate the plane somewhere between kilometer 2788 and 2798—a considerable reduction in your uncertainty about its position.
Now imagine that you had already exhausted all the information available about the plane prior to your measurement—perhaps you only have a limited amount of memory to store your data. What happens once you hear its engine roar, and place it within a 10 km interval? Well, if you increase your information about the position of the plane, yet your memory is already maxed out, the information you have about another aspect of the plane must decrease, at least as much as your information about its position has increased. Since the only other quantity available is the plane’s speed, then, an increase in information about position entails a decrease in information about its speed—which, to the quantum literate, should start to sound familiar: and indeed, this is nothing but Heisenberg’s famous uncertainty principle.
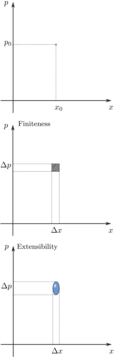
It is useful to imagine this pictorially. TWA 702, if you have limited information about its state, is located within some area of uncertainty on the two-dimensional plane, rather than pinned down to a single point whose coordinates yield exact values for position and speed. The uncertainty principle then says nothing but that this area can never decrease—if you increase your information about the plane’s position, it is ‘squeezed’, yielding a compensating decrease of information regarding its speed. The size of this area, as pointed out by Carlo Rovelli in his ‘relational’ reconstruction of quantum mechanics, is given by nothing but Planck’s famous quantum of action, typically denoted ℏ (read: h-bar).
Moreover, suppose we carry this to the extreme: say a sudden parting of the clouds allows you to perfectly measure the plane’s position. Then, the area is maximally distorted, becoming ‘infinitely long’ along the speed-axis: a plane perfectly located has a completely indefinite speed. Conversely, measuring the plane’s speed perfectly entails maximal uncertainty regarding its position—the plane becomes delocalized (which would make the plane a plane wave, mathematically—quantum states with perfect ‘speed’-information are waveforms in space).
This is the reason why we can either observe particle-like or wave-like behavior in quantum systems, but not both: thus, in the classical double-slit experiment, when we try to sneak a peek at which slit the particle traverses, it ceases to be wave-like distributed through space, and can no longer self-interfere.
We seem off to a good start: the two principles have given us a shortcut to several intriguing quantum phenomena, without ever having to talk about branching worlds or collapsing wave-functions. But there is still an air of arbitrariness to them. Who has decreed that there ought to be a maximum amount of information? We seem to have achieved little but replacing a God who plays dice with one who won’t show his cards.
Letting the Cat out of the Box

If you know the first thing about quantum mechanics, you know the story of Schrödinger’s cat. This thought experiment was conceptualized by Austrian physicist Erwin Schrödinger, one of the founding fathers of the theory, as an illustration of the ‘ridiculous cases’ one can set up within the theory. Said cat, by the nefarious designs of some cruel experimenter, has been imprisoned in a closed box, with a peculiar apparatus: upon the decay of a single atom in a small quantity of radioactive matter, an automatic can opener is activated, opening a can of cat food—or failing to, as the case may be. Within a certain period of time, with 50% probability, the atom either decays, or doesn’t, the can is opened, or stays closed, and the cat is fed, or goes hungry (there’s never any reason for undue animal cruelty, not even in thought experiments).
Schrödinger devised his thought experiment to highlight the curious fact that quantum theory cannot decide which of these options in fact comes to pass: the atom, and with it, the can of cat food and the cat itself, are described by a superposition of both options—and it’s only upon opening the box, thus ‘measuring’ the state of the cat, that this curious state resolves itself into a cat that’s either licking its chops or complaining about the lack of service. That is, the state of the system before the box is opened is consistent with either option, but fails to uniquely decide which will obtain.
Perhaps it was this sort of situation that sparked a certain recognition within Wheeler: the complete specification of a system fails to uniquely fix all its properties—boiled down to its essence like this, it sounds suspiciously similar to the logical bomb dropped by a young Kurt Gödel on the very project of finding a complete and consistent system of mathematics, just a few years before Schrödinger devised his cat-tale.
More precisely, what Gödel had shown was that, for certain mathematical systems capable of ‘talking about themselves’ in a certain sense, there will always be undecidable propositions—that is, statements in the system’s language that it can neither prove true nor false. Much of the ingenuity of Gödel’s proof lies in the way he fed a mathematical system back into itself. Working within the theory of natural numbers, he proposed a sort of ‘code’ assigning a number to statements within the theory (now known as a ‘Gödel numbering’). Using this, the theory of the natural numbers can be folded back on itself: proofs concerning the properties of certain numbers then implicitly refer to statements within the theory itself.
Thus, there can never be a single mathematical system capable of encompassing all mathematical truths—demolishing the program originated by one of the towering figures in mathematics of the early 20th century, David Hilbert.
In mathematics, since the work of Euclid, a theory is given by means of a set of axioms—crisp statements of unquestioned validity that are taken as encapsulating a compressed, but complete specification of the theory. Euclid’s own object was plane geometry, whose elements are points, lines, angles, and so on. Of these, he required certain properties—such as that there exists a line joining any two points, or that any two lines intersected by a third at less than right angles eventually intersect one another.
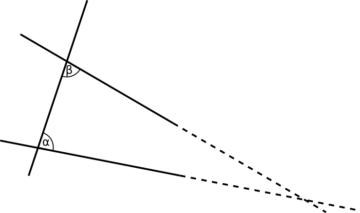
This latter statement is the famous parallel postulate: as a consequence, parallel lines on the plane never intersect. It turns out that there are geometries in which the parallel postulate doesn’t hold, but Euclid’s other postulates do, such as on the surface of a sphere. Thus, those other axioms on their own don’t uniquely specify the domain they apply to: whether parallel lines intersect or not is left open by them—it’s undecidable.
Such undecidability, Gödel had proved, exists in every mathematical system of a certain complexity—thus, any such theory leaves certain properties of its domain open. Just as both plane and spherical geometry ‘fit’ Euclid’s first four postulates, so does every mathematical theory have multiple objects (in mathematical parlance, ‘models’) that fit it. We may then imagine Wheeler wondering: could this be related to the fact that both a hungry and a well-fed cat ‘fit’ with the quantum theoretical description of Schrödinger’s box?
I believe this question can be answered affirmatively, and have proposed a formal argument to this end. In the next column, I will try to trace its outlines, and argue that the ‘weirdness’ of quantum mechanics is ultimately just the impossibility of surveying the whole world from a singular perspective.
