by Jonathan Kujawa

In May of 2020 we lost John Conway [0]. We discussed some of his mathematical accomplishments here at 3QD. He was a true original.
At the time, I deliberately avoided discussing Conway’s most famous work: the Game of Life. Like a 60s rock band, Conway had mixed feelings about his most famous hit. But like hits that stand the test of time, it deserves its reputation. The Game of Life still has surprises and mysteries for us nearly sixty years after its invention. I thought it’d be worth talking about some of the latest discoveries.

Conway invented the rules of Life in the late sixties. According to Wikipedia, Conway was simultaneously motivated by Stanislaw Ulam’s work on the growth of crystals and by parallel investigations by John von Neumann on self-replicating systems. For the former, I highly recommend the Crystalverse website for instructions on growing your own crystals. For the latter, think of robots who can build more copies of themself like these Xenobots.
Ulam and von Neumann worked at the Los Alamos National Lab in the 1940s and 50s. They could only dream of Xenobots. Instead, as a simplified model, both assumed that they were working in two dimensions, and both space and time could be chopped up into discrete, irreducible parts. They were interested in what sorts of dynamical, self-organizing processes could happen in such a world.
That’s it.
The only thing left is to set the rules for this world.
This world is so stripped down, it’s reasonable to expect it would take an elaborate set of rules for anything interesting to happen. To create self-growing “crystals” or self-replicating “objects” in this world will surely require an elaborate and lengthy set of rules. After all, the biology of life on Earth is tremendously complicated.
A mathematician like Conway knew that sometimes elementary rules give rise to incredibly complicated structures. As we discussed two years ago, Conway was a group theorist. A group has only three simple axioms. Despite this (or perhaps because of this), groups are rich objects which have been studied for more than a century and which have all sorts of applications to the real world. Likewise, Euclid’s five postulates are enough to generate an entire geometry.
So Conway played with the rules of this world.
I used to feel guilty in Cambridge that I spent all day playing games, while I was supposed to be doing mathematics. Then … I realized that playing games is math.
— John Conway
Ever simplifying, Conway managed to get down to two simple rules:
- If, at a given second, a living cell has 2 or 3 living neighbors, it stays alive for the next second. Otherwise, it dies [2].
- If, at a given second, a dead cell has exactly 3 living neighbors, it comes to life in the next second. Otherwise, it stays dead [2].
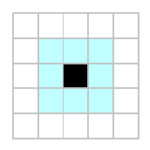
That’s it. One little region of this world is in the grid image posted above. The black center cell is alive in the current moment — whether it lives or dies depends on the status of its 8 neighbors (the aqua colored cells). This is Conway’s Game of Life.
From these two simple rules, entire worlds are created. All you need to do is set up an initial configuration of living and dead cells and then apply the rules as time ticks forward. For example, here is an arrangement of living cells that will forever generate a stream of little “gliders” that zoom off to the southeast.
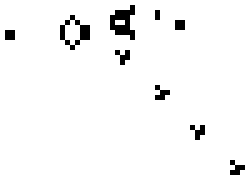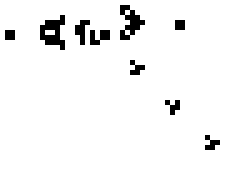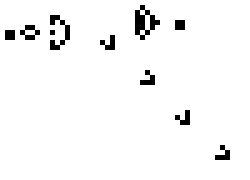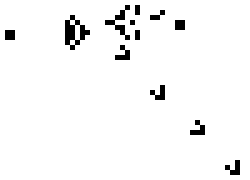
This isn’t quite self-replication, but surely von Neumann would have been impressed with such a simple object generating gliders forevermore [3].
I mentioned that the Game of Life is studied to this day. Indeed, there is an entire community of amateur and professional computer scientists, mathematicians, and curiosity seekers who are investigating what can be done in the Game of Life. In addition to a book by Johnston and Greene [1], there is an entire website devoted to world-building within Life. The vocabulary they’ve invented to describe their creations is Tolkien-esque:
The quadpole is more common than the tripole in random soup, due to a relatively common bottleneck reaction involving a century variant hitting a ship.
— a “fun fact” from the Conway Life website
Conway’s initial investigations probably involved reams of graph paper, but now we usually let a computer do the tedious work of applying the rules of Life. Indeed, you can run the Game of Life in your browser on the Conway Life website.
What have we discovered recently? In January, David Raucci constructed the first oscillator of period 38. That is, like how the hands of a clock repeat themselves every 12 hours, Raucci discovered a pattern of living and dead cells which repeats itself every 38 seconds in the Game of Life. As of today, we still don’t know if there are oscillators with period 19 or 41.
Also this year, Ilkka Törmä and Ville Salo, researchers at the University of Turku in Finland, discovered the following configuration:

This answers questions Conway himself asked in 1992. Conway was curious both about the existence of static patterns, and about the possibility of patterns which could provable not have come from other patterns. Here it is thirty years later and we’re still wrestling with puzzles given to us by Conway.
It is perhaps not surprising that the Game of Life is such a rich world. In 1982 Conway proved that the Game of Life is a (finite) universal Turing machine. That is, using an appropriate configuration of cells the Game of Life can be used to perform any computation and, hence, can simulate any computer. This makes the Game of Life as complicated as anything you can imagine a computer doing. If you find yourself on a desert island with a vast quantity of graph paper and time, you could even use the Game of Life to play Tetris.
[0] Conway died from covid-19. According to Johns Hopkins University, 6,500,000 people have died worldwide from covid-19 (the WHO estimates 15,000,000 excess deaths during the time of covid). According to the NY Times, in the US alone there have been more than 1,043,000 deaths with 400-500 more every day.
[1] Image borrowed from the book “Conway’s Game of Life: Mathematics and Construction” by Nathanial Johnston and Dave Greene. They’ve generously made the entire 500-page book available as a free download here. It contains (nearly) everything you could possibly want to learn about the Game of Life.
[2] You can imagine that if a cell has 0 or 1 living neighbors, it dies from loneliness; if it has 4 or more living neighbors, it dies from overcrowding. Likewise, if a dead cell has just the right number of living neighbors, then it is stimulated into life.
[3] Remember, to avoid complications we assume our grid is infinite in every direction. The grid is only truncated in this image because it has to fit into the pages of 3QD. These gliders will continue to head to the southeast forever.
