by Jonathan Kujawa
Some years ago I twisted the arm of an old friend and got him to visit Oklahoma to give a talk to several hundred high school students. Any reasonable person would be terrified at the idea of facing a crowd of teenagers to tell them the wonders of mathematics. Gladiators in the Colosseum had better odds. Fortunately, Michael Orrison is not a reasonable person. He handled the job with aplomb.

100 ants are dropped on a meter stick. Each is traveling to the left or right with a constant speed of one meter per minute. When two ants meet, they reverse direction and head away from each other. When an ant reaches the end of the meter stick, it falls off. What is the longest amount of time it takes for all 100 of the ants to fall off the meter stick?
At first and second glance, this seems like a very difficult problem. There are 100 variables for the locations where the ants first land on the stick, plus another 100 variables recording if they first go left or right. There will be all sorts of ping-ponging back and forth and the ants will only slowly drop off the meter stick one by one. It isn’t even so clear that you couldn’t arrange a scenario where a few ants oscillate back and forth forever. With some thought, you can convince yourself that never happens. Still, it still seems like a very hard problem to compute how long it might take for the meter stick to empty of ants.

One of the other themes of Michael’s talk was the importance of considering symmetry [2]. While talking to the high school students Michael pointed out that even if you don’t care a wit about mathematics, symmetry is everywhere. It influences what we find beautiful, affects how we design and build things, and even plays a crucial role in the conservation laws of physics [3].
As Michael told the students, even if you are, say, a ballet dancer you should care about symmetry as it can inspire new dance moves: instead of moving your left leg, move your right; instead of stepping forward, try stepping back. Our bodies and the 3-dimensional space they inhabit naturally have symmetry. Being mindful of this symmetry can inform you of what is possible and what is impossible. The left-right symmetry of your legs suggests you shouldn’t move both legs to the left [4].
I was reminded of Michael’s talk when reading a recent article by my fellow Oklahoma-based mathematician, Henry Segerman. We ran across Henry in an earlier 3QD essay. Henry is a topologist by day but is a mathematical artist by night. In fact, he’s written an entire book on how to use 3D printing to explore the intersection of art and mathematics. Recently, though, Henry has gone to something on a bigger scale.

As you can see, German wheels very much want to roll back and forth in only one direction. If the acrobat isn’t careful, like Michael’s ants, the acrobat will roll themselves right off the end of the stage. This leads to a necessary bit of awkwardness: the acrobat is forced to incorporate deliberate stops, turns, and reversals into their routine to avert disaster.
Maybe symmetry can help us here. The reason the Wheel rolls so easily in one direction and so poorly in all the others is because it has a lot of rotational symmetry in one direction but not the others. With this defect in mind, Toni Vighetto invented the Zigrolling apparatus (pictured at the top of the page). The outer frame is two wedges of a sphere oriented in opposite directions so that you can roll in multiple directions. You can see it in action in this video.
As its name suggests, the Zigrolling apparatus will zigzag as it is rolled along the ground. An idealized version of the apparatus is what mathematicians call a sphericon. Its rolling path is this:
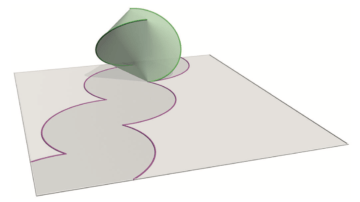
If you do a complete rotation you are pointed in the same direction as you started. On a large scale, the Zigrolling apparatus also travels in a straight line and will tip you off the edge of the stage if you give it the chance.
While at a juggling convention Henry met Marco Paoletti, who asked Henry if it was possible to design a rolling acrobatic device that would naturally turn of its own accord as it was rolled along.

For example, if you were to roll a cone along the floor it would tend to turn as it rolled and eventually end up back where it started. Of course, a cone wouldn’t be very practical for acrobatic routines as it would be hard to steer around the stage.
The problem with Marco’s question is that there are many possible shapes that seem plausible to try. As we saw in this 3QD essay, there are all sorts of shapes that can roll smoothly along a stage (like the Meissner tetrahedron). It’s certainly not practical to build hundreds of prototypes and try them out!
Michel Orrison’s advice here would be to look for new points of view which can shed light on the problem. As a mathematician, Henry Segerman knows well to apply this strategy.
First, Henry made the reasonable assumption that the center of mass of the apparatus should always be the same height off the ground. If it wasn’t, then when the center of mass was higher, the apparatus would tend to be unstable. And when the center of mass is at its low point the apparatus would be too stable and would require extra force to push out of that position. You could build unbalanced devices, but then acrobats wouldn’t want to use them.
Henry then imagined the device as contained in a sphere: the center of mass would be the center of the sphere and the stage would touch the surface of the sphere. If the stage had a thin coat of paint, then as the device rolled across the floor a thin line of paint would leave a path on that imaginary sphere. Likewise, there would be a trail left in the paint as the device rolled by.
Marco’s question, then, was a question of determining if and when the path on the stage was bounded or unbounded. That is, if the device is rolled in one direction, does the path of the device head off into the distance without constraint (like the German Wheel or the Zigroller) or does it stay within a constrained space?
Put this way the problem still seems hard. Henry realized, however, that questions about the path on the stage should be reflected in questions about the path drawn on the surface of the sphere. That is, the seemingly unconstrained problem of describing a path on a possibly infinite stage can be recast as a constrained problem on the surface of the sphere. The power of using math to see the world differently!
Applying tools from geometry, Henry showed that the device will need an unbounded stage if and only if the path on the surface of the sphere exactly cuts the sphere into two pieces of equal area [6]. The path of the German Wheel goes around the equator of the sphere. As the Zigrolling apparatus rolls along it leaves a path on its imaginary sphere which would be the seam if the sphere were a tennis ball. Since that splits the area of the sphere in two the device must roll in a straight line:
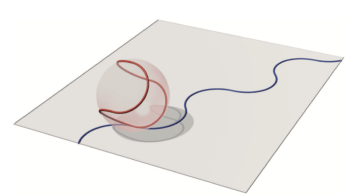
Here the red line is the path on the imaginary sphere where it touches the ground as it rolls and the blue line is the path made on the ground.
Of course, most paths around a sphere do not split it into two equal halves. In short, Henry showed that the German Wheel and the Zigrolling apparatus are actually rare exceptions!
Of course, Henry wasn’t satisfied with just answering the question in theory. He also used the mathematics of symmetry to show how to design rolling devices which do circle back around and do so in lots of interesting ways. For example, by making the tennis ball seam of the Zigroller a little less symmetric, Henry designed a Zigroller variant that returns to its starting position after three complete revolutions:

In this picture, the green lines are the “rails” where the device will actually touch the ground as it rolls, the purple lines are where the rails touch the ground, the red line is the path on the imaginary sphere, and the blue line is the path on the ground made by the imaginary sphere.
Using mathematics, Henry can now design an acrobatic apparatus with specific rolling behaviors pre-built into the device. And this is not just theoretical! Henry worked with Lee Brasuell to design and build a full-scale acrobatic device which is called the Tao-line apparatus (the path on the imaginary sphere drawn in red above makes an image that looks rather like the yin and yang symbol). It’s been used by performers to good review. You can see it in action in this video.
[0] Image borrowed from here.
[1] Image borrowed from here.
[2] Both Michael and I do research in the area of representation theory. This is the study of the role of symmetry in mathematics and in its applications to other fields. So we might be a little biased here :-).
[3] One of my personal heroes is Emmy Noether. As a mathematician, I claim her for her important work in abstract algebra, topology, and algebraic geometry. But physicists tell me she should be equally known for the Noether Theorem in physics. See Tasneem Zehra Husain’s 3QD essay here for a discussion of Noether’s work.
[4] Unless, of course, you are Buster Keaton.
[5] Image borrowed from here.
[6] There are other technical assumptions in play here. For example, Henry assumed the path on the sphere eventually returned to where it starts, and that it doesn’t have any abrupt turns or self-crossings.
