by Jonathan Kujawa
In my last essay for 3QD we talked about how we are at the beginning of a new era in mathematics. As a discipline mathematics has the mythos that it is True and Eternal, but it is also a human endeavor and has its share of errors. Fortunately, it is a robust and self-correcting system that usually catches and corrects these errors.
For several decades we have had proof verification software. Versions of such software are useful in the so-called “real world”. NASA, for example, is keen to avoid software crashes. After all, if you brick the Curiosity rover on the surface of Mars it’s not like you can just reboot it. NASA sponsors an ongoing series of meetings devoted to formal verification methods.
In mathematics, however, proof verification software has yet to play an important role. For both human and technical reasons, research mathematicians and proof verification folks live on different planets. My last essay was about the software package Lean and the fact it is quickly getting up to speed with undergraduate level mathematics and even knows about manifolds and perfectoid spaces (geometric objects used by researchers every day). Heck, perfectoid spaces were introduced by Peter Scholze less than a decade ago — a blink of an eye in the long arc of mathematics.
In fortuitous timing for 3QD readers, Lean made news just last week. In December Peter Scholze laid down a challenge to the Lean community. It was called the Liquid Tensor Experiment. Last week the challenge was answered.
The revolution has begun!
In brief, Dr. Scholze and his collaborator Dustin Clausen have an important, albeit technical, result and they want every mathematician to be absolutely, completely, unreservedly confident it is correct. They also have a proof of the result and six months ago they were 99.9% certain the proof was correct. But 99.9% is not 100%. As I’ll explain in a moment, it is important we have 100% certainty the result is correct. Here’s Scholze’s challenge:
Why do we care about this technical result of Drs. Clausen and Scholze? Why did the Lean community rise to his challenge?
Several years ago Dr. Scholze and Dustin Clausen proposed a significant change to the very foundations of mathematics. In certain research areas they are interested in, they want to replace topological spaces with something they call “condensed sets”. Topological spaces are the basis of a loose form of geometry where you ignore absolute distance and instead focus on more relative notions of distance and questions like who is connected to whom. We talked about topology and its usefulness here at 3QD.
Oftentimes in mathematics, you find yourself studying something which happens to also be a topological space. For example, the real numbers have an addition operation which makes them a group [3]. But there is also a notion of distance on the number line which gives you geometry and, hence, makes the real numbers a topological space. Taken together this makes the real numbers a “topological group”. The problem is that topological groups as a concept aren’t always well-behaved. There are various constructions and operations you might want to do with topological groups but don’t make sense or, if they do, give you things that, morally, should again be topological groups but aren’t [4]. The conjunction of topology and group theory is a fragile concept. The proposal of Drs. Clausen and Scholze is to replace topology with the more robust notion of condensed sets. They want us to study condensed groups instead of topological groups.
Drs. Clausen and Scholze gave an entire course on “condensed mathematics”. They explain their ideas, how it works in practice, and why it is the right notion to replace topology. I have to admit I only dimly followed their first few lectures. It would take concentrated study to grasp what all they are doing here.
As a highly respected leader in mathematics, Dr. Scholze’s ideas are taken seriously [1]. But mathematicians are also a conservative bunch and don’t change their core definitions at a whim. In particular, if you are going to swap out a pillar of knowledge you want to know mathematics will remain standing after you are done [2]. To get others to invest time into your ideas, it would be a big help if you can say with certainty that they are a positive gain for mathematics as a whole.
I know topology and groups pretty well. I’m not going to spend much time on condensed groups until I’m convinced it’s both correct and useful. I long ago learned that there are things which are true but not useful and things which could be useful but aren’t true. Something needs to be both true and useful to be worth getting out of bed for.
Drs. Clausen and Scholze identified Theorem 1.1 as a key step to their program of condensed math. It is definitely useful. Assuming it’s true, it leads to all sorts of important results in real functional analysis (a central area of modern mathematics). With Theorem 1.1 Drs. Clausen and Scholze are able to provide compelling evidence that condensed math can still support modern mathematics.
The problem is that they had sweated for months and months and still couldn’t say with 100% certainty that Theorem 1.1 was true. It almost certainly was, but their arguments had subtle points where doubts could linger. A counterexample cockroach can squeeze through the tiniest of gaps.
This led to Dr. Sholze’s challenge to the Lean community. He said, “Here’s a mathematical statement and knowing if it is true or false is of real importance. Care to help us out?” My impression is that there was no real expectation that anything would come of it, at least not for several years. Proof verification is only just now getting to the stage where it can handle modern research questions. Worse, condensed mathematics is an entirely new thing. Not one drop was in Lean a year ago.
Nevertheless, Johan Commelin took up the challenge. In a tour-de-force of effort Dr. Commelin and others successfully used Lean to verify the validity of Theorem 1.1! They had to teach Lean the relevant bits of condensed math and implement the Scholze-Clausen proof of Theorem 1.1. They did so and showed that it is 100% correct. Well, that was a lie. Dr. Commelin hasn’t yet verified Theorem 1.1. So far he has only verified Theorem 9.4 on page 56 of these notes. However, Dr. Scholze says that his 0.1% of worry about the proof of Theorem 1.1 was concentrated on this Theorem 9.4. With this in the bank, he’s confident the rest should go without a hitch. It will come as a real shock if the verification fails after this.
Here is their roadmap to proving Theorem 9.4. Green means the result has been verified in Lean. All green means Theorem 9.4 itself has been verified:
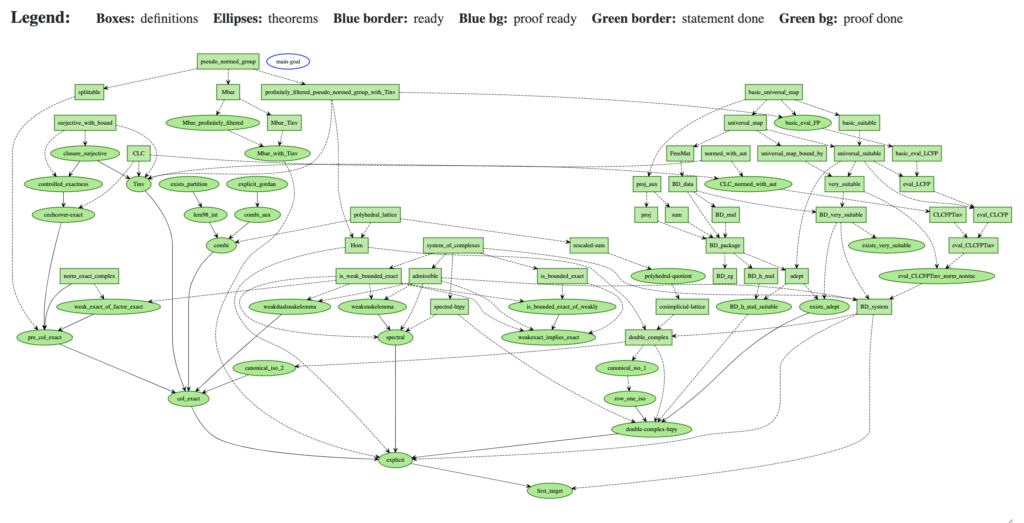
The revolution has begun!
Lean was used to verify an important mathematical result we weren’t 100% sure of.
This is an important moment in mathematics. It is not hard to imagine a future where proof verification is a standard part of the mathematician’s toolkit. There will be a learning curve and it may take a generation or two, but it will become common for mathematicians to provide a formal verification of their papers.
My undergraduate advisor wrote the greek symbols for his research papers by hand. Nowadays everyone does full-on typesetting using LaTex. My students’ students will shake their heads at how Old Man Kujawa used to check proofs line-by-line!
I have refereed for countless math journals over the years. A painful part of refereeing is making an honest effort to provide a “human verification” of the paper’s results. When I was young I checked papers line-by-line. Now with more experience and less time, I satisfy myself with checking what I consider to be the crux points of the paper [5].
It would be an absolute dream to referee for a journal that required submissions to be formally verified. The referees, editors, and readers would all have confidence the results are correct and it would simply be a question of if they are useful and interesting.
Also, it is still an unsettled question whether the abc Conjecture is proven or not. Mochizuki and his collaborators claim to have a proof, but it hasn’t convinced others in the field [6]. The entire question could be settled using Lean.
This is not to say that mathematical proofs will become irrelevant! As Animal Symbolicum, Roger, and I discussed in the comments of my last essay, a proof for proof’s sake is quite unsatisfying. The purpose of a proof is to verify, but also to illuminate. The goal of mathematics is to understand after all.
The good news is that proof-verification can help here as well. As Dr. Scholze wrote in reply to a question about what he learned from the proof formalization in Lean:
What actually makes the proof work! When I wrote the blog post half a year ago, I did not understand why the argument worked, and why we had to move from the reals to a certain ring of arithmetic Laurent series. But during the formalization, a significant amount of convex geometry had to be formalized (in order to prove a well-known lemma known as Gordan’s lemma), and this made me realize that actually the key thing happening is a reduction from a non-convex problem over the reals to a convex problem over the integers.
The very act of formalization gave new understanding. This is a long way from the mathematical Dæmons of my last essay, but there is a not-so-distant future where computers provide significant value to researchers and the Luddites will quickly fall behind.
I, for one, welcome our proof-verification overlords.
In another coincidence, this weekend I listened to an interview of Sam Altman by Ezra Klein. Sam Altman the CEO of OpenAI, one of the leaders in Artificial Intelligence. The future Altman envisions is equal parts amazing, alarming, and fanciful. Altman sees a future where computers can do what they are told and solve any problem we ask of them, but also solve problems we haven’t even thought of.
It would be the end of the Ted Nelson era of computing:
The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do. — Ted Nelson
The interview is worth a listen. If there is even a chance of such a future, we should be thinking seriously about what that future should look like.
[1] After all, Dr. Scholze invented/discovered perfectoid spaces and they’ve revolutionized big chunks of mathematics. He received the Fields Medal in 2018 for this work.
[2] Here in Oklahoma, most houses — including ours — are built on clay soil. Clay expands, contracts, and moves as its moisture content changes. Most houses in town have cracks in their walls from all the moving and shifting. The only solution is to drive piers deep into the ground under your home until you hit bedrock. It’s a huge amount of work and, when it is all said and done, your house is back to where it started, but it now has a stronger and more robust foundation. There’s a metaphor in there somewhere.
[3] In mathematics, a “group” simultaneously abstracts the concept of a number system and the concept of the symmetries of an object. We talked about groups here on 3QD.
[4] This is not just a problem for topological groups; topological rings, topological vector spaces, and various similar gadgets have similar problems.
[5] Similar to Dr. Commelin’s verification of Theorem 9.4. Checking Theorem 9.4 doesn’t get us to Theorem 1.1, but that was the real spot of worry. If it checks out, the rest is probably also fine.
[6] In another coincidence, Peter Scholze is prominent among those skeptical of Mochizuki’s proof. His experience talking with Mochizuki about his proof probably explains why he was so keen to get Theorem 1.1 verified!