by David Kordahl

James Clerk Maxwell, whose theory of electromagnetism occupies the same physics pedestal as Newton’s theory of gravity, was by all accounts a good-humored and generous man, and a fairly confusing lecturer. Here is a story about Maxwell (admitted to be apocryphal in the math notes that recount it) that suggests something of his character:
Maxwell was lecturing and, seeing a student dozing off, awakened him, asking, “Young man, what is electricity?” “I’m terribly sorry, sir,” the student replied, “I knew the answer but I have forgotten it.” Maxwell’s response to the class was, “Gentlemen, you have just witnessed the greatest tragedy in the history of science. The one person who knew what electricity is has forgotten it.”
This anecdote—this joke—is improved for those who know Maxwell as the preeminent early theorist of electricity. After all, if Maxwell didn’t know how to define electricity, what hope was there for his students?
At risk of over-explaining it, this anecdote gestures toward a piece of insider knowledge. You don’t need to know everything to construct a mathematical theory, and mathematical theories can be more robust than the systems they have been constructed to describe. As I’ve written elsewhere, mathematical techniques that are useful in one area of science tend to be useful in in other areas, not as an exception, but as a rule.
Two recent books from Princeton University Press deal in fundamentally different ways with the need to press forward under uncertainty. In Hot Molecules, Cold Electrons: From the Mathematics of Heat to the Development of the Trans-Atlantic Telegraph Cable, Paul J. Nahin quotes the above Maxwell anecdote verbatim, and adds, “It may be apocryphal, but even if it is, it honestly reflects the present state of our (lack of) understanding.” In Nahin’s presentation, the physical world is not easily known, but the mathematics we use to represent the world can be clearly and elegantly explained, allowing the same tricks to be used from the early theory of heat conduction (the title’s “hot molecules”) to the later developments in electrical signal propagation (the title’s “cold electrons”).
A. Zee’s Fly by Night Physics: How Physicists Use the Backs of Envelopes takes nearly an opposite tack. As he explains in the preface, Zee wants to give physics undergraduates the joy of knowing “that physics is capable of describing the real world!” To this end, he zooms around quickly and uses just as many equations as one might be able to fit on cocktail napkins during an overnight flight. As he comments early on, “Undergraduates typically get the impression that physics progresses logically, and every result is derived step by step. Surely, dear reader, you know that this is often far from the truth. A truly profound advance in physics involves a leap of faith, a wild but educated guess.”
Each approach has its merits, but Nahin certainly has the better manners. It’s not easy to write expository mathematics, and I suppose the best recommendation of Cold Molecules, Hot Electrons is to admit that, immediately after finishing it, I bought another of Nahin’s many books.
Nahin is a practiced pedagogue, combining historical background and technical dosh with a Maxwellian good humor. Opposite the title page, portraits of Joseph Fourier and William Thompson are printed under the header, OUR TWO HEROES. “Fourier and Thomson were enormously clever analysts,” Nahin writes in Chapter 1, “and since my intention in this book is to weave the historical with the technical, everything you read here is just how either man might have written this book.”
The main trick Nahin explores in increasing levels of detail is that of Fourier decomposition. Suppose that you have a math problem whose very simplest version can be solved using sines and cosines. The main idea of Fourier decomposition is to rewrite the general solution in terms of these simpler solutions. Often this will give you a solution that involves an infinite number of partial solutions to add up, but engineers are often content just to sum up the first few and call it a day.
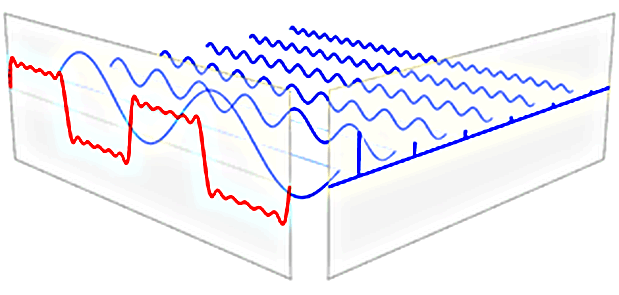
An illustration of Fourier decomposition from Wikipedia: a general signal (in red) is given by the weighted sum of many sinusoids (in blue).
Fourier developed a theory of how heat spreads, but we are shown by the book’s end that the same mathematical tools were able to describe how electronic signals smear out as they propagate along telegraph cables. Why would these tools work for both cases? Well, in this case it’s less a matter of the same thing happening in each case (hot molecules are not cold electrons), as of simple models being useful across domains.
Of course, simple is a relative term. Nahin has written a book in which he intends to use “nothing but high school AP-calculus,” and while this is technically true, I suspect that most high-schoolers reading it would find the book pretty tough going—but not for Nahin’s lack of trying.
Fly by Night Physics, on the other hand, makes no such concessions. As Zee explains in the preface, his emphasis is on “fun,” so he has written a book that “is not for the students shaky in their mastery of the basics and hanging on by the skin of their teeth.” Zee writes with an air of simplicity that skirts just how much background he expects his readers to have. The conceit, here, is to to assume that the reader is an ideal undergraduate (a teenaged Zee?), who understands all the standard physics lore but just needs one last push. Naturally you know X, but did you ever realize Y?
This all might be okay for physics majors entering graduate school, but I suspect the main readers of Fly by Night Physics will be professors. Zee expects his readers to have met him already (allusions to his past textbooks are scattered throughout), and to have imbibed the culture of physics (“Dyson has remarked,” begins one section, and we are left to infer this as Freeman Dyson). 400+ pages of this is at once a treat and a chore, like cake for supper. I gave up a straight read-through around page 150 and plan to revisit subjects when I need to teach them.
Zee opens his books with a quote that he claims to have been told, as a freshman at Princeton, by John Wheeler: “Never never calculate unless you already know the answer!” And this is the attitude he takes throughout, swashbuckling through vast fields with few pedagogical pauses.
Consider Chapter VIII, “From surfing to tsunamis, from dripping faucets to mammalian lungs,” which begins with an educated guess about how water waves will propagate differently in deep vs. shallow water. This guess is connected to why waves always seem to refract toward the beach near the shore, and why waves crest in shallow water. New physics for water waves emerges at short wavelengths from the relationship between surface tension and surface curvature, which leads to a size estimate for the droplets of a leaky faucet. After a discussion of evolutionary trade-offs in animal lungs, material on drag and viscosity closes out the section.

Water physics. Left: a wave crests when its top travels faster than the wave speed in shallow water. Right: capillary action’s limited ability to overcome gravity puts an upper limit on tree height.
That’s a lot to cover in thirty pages with ample white space! Yet Zee is able to pull it off, and his insouciant tone makes it all seem easy.
The books by Nahin and Zee are nearly opposites in tone and structure, with Nahin carefully developing his self-contained presentation towards a modest goal, and Zee wildly claiming that good guessers might scoop some of physics’ greatest triumphs. I’m not sure I would buy some of Zee’s quick-and-dirty derivations without having first seen the standard treatments, but no matter. Allowing stylistic differences to flourish is the least we can do in approaching the mysteries of physics. As Zee reminds us, “the truly major advances are often made, almost by definition, in the absence of an established theory during a time when confusion reigns.”
