by Jochen Szangolies
Thomas Bayes and Rational Belief

When we are presented with two alternatives, but are uncertain which to choose, a common way to break the deadlock is to throw a coin. That is, we leave the outcome open to chance: we trust that, if the coin is fair, it will not prefer either alternative—thereby itself mirroring our own indecision—yet yield a definite outcome.
This works, essentially, because we trust that a fair coin will show heads as often as it will show tails—more precisely, over sufficiently many trials, the frequency of heads (or tails) will approach 1/2. In this case, this is what’s meant by saying that the coin has a 50% probability of coming up heads.
But probabilities aren’t always that clear cut. For example, what does it mean to say that there’s a 50% chance of rain tomorrow? There is only one tomorrow, so we can’t really mean that over sufficiently many tomorrows, there will be an even ratio of rain/no rain. Moreover, sometimes we will hear—or indeed say—things like ‘I’m 90% certain that Neil Armstrong was the first man on the Moon’.
In such cases, it is more appropriate to think of the quoted probabilities as being something like a degree of belief, rather than related to some kind of ratio of occurrences. That is, probability in such a case quantifies belief in a given hypothesis—with 1 and 0 being the edge cases where we’re completely convinced that it is true or false, respectively.
Beliefs, however, unlike frequencies, are subject to change: the coin will come up heads half the time tomorrow just as well as today, while if I believe that Louis Armstrong was the first man on the moon, and learn that he was, in fact, a famous Jazz musician, I will change my beliefs accordingly (provided I act rationally).
The question of how one should adapt—update, in the most common parlance—one’s beliefs given new data is addressed in the most famous legacy of the Reverend Thomas Bayes, an 18th century Presbyterian minister. As a Nonconformist, dissent and doubt were perhaps baked into Bayes’ background; a student of logic as well as theology, he wrote defenses of both God’s benevolence and Isaac Newton’s formulation of calculus. His most lasting contribution, however, would be a theorem that gives a precisely quantifiable means of how evidence should influence our beliefs.
The theorem that now bears his name was never published during the lifetime of Thomas Bayes. Rather, it was his close friend Richard Price who discovered Bayes’ writings among his effects and published them under the title An Essay towards solving a Problem in the Doctrine of Chances. Especially interesting, however, is the use he intended to make of his friends’ formula: in 1748, David Hume had published his seminal Enquiry Concerning Human Understanding, in which he lays out several skeptical challenges—amongst others, against the notion of miracles.
While it is unclear whether Bayes himself intended to mount his reasoning against Hume’s skepticism, Price puts it to just that use in his essay On the Importance of Christianity, its Evidences, and the Objections which have been made to it. Essentially, he argues that Hume does not appropriately take into account the impact of eye witness testimony for judging the likelihood of the occurrence of miracles—in other words, fails to properly update his beliefs.
But how, then, does Bayes’ theorem work? Rather than giving a complete introduction, let’s look at a simple example. Suppose there are two jars of cookies. In one jar, A, half of all cookies are chocolate chip cookies; in jar B, only one in ten is. You reach into one of the jars at random, and, happily, draw out a chocolate cookie. What is the probability that this is jar A?
The question, in other words, is one about how new data C—drawing a chocolate cookie—should influence your belief in a certain hypothesis A—that this is jar A. Before obtaining said data, you would be justified, having chosen a jar at random, in assigning a likelihood of 50% to A—written P(A) = 50%.
This likelihood before having obtained any data is sometimes called the ‘prior’, and in case we assign equal probability to each of an array of options, a ‘uniform’ or ‘uninformative’ prior—in fact, an instance of the Principle of Indifference we’ve already met. Our issue is now how that probability changes—that is, how we transition from P(A) to P(A|C), the likelihood that A (‘this is jar A’) is true given the data C (drawing a chocolate cookie).
New data can either increase or decrease our confidence in a hypothesis; moreover, different sorts of data are differently informative regarding the hypothesis. Precisely how new data shapes our confidence in the hypothesis is given by Bayes’ famous formula:
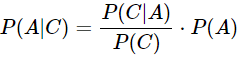
This formula precisely quantifies how new data, new evidence, new experiences should shape our beliefs, our ‘model’ of the world—provided we are acting rationally. Our confidence increases with a high likelihood of the data arising, given that the hypothesis is true—P(C|A)—, as such data confirms the hypothesis, and increases more strongly with unlikely data—P(C) being small—, since such data carries more information. For the example worked in detail, see the box below.
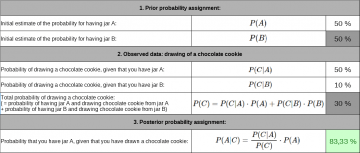
There are several important conclusions to draw from this. First, whether certain evidence is convincing to you depends on your beliefs going in—while drawing a chocolate cookie in the case of indifference between the jars serves to tip the balance towards believing you have jar A in your possession, if you had had reason to believe, initially, that you have jar B, then you might not be convinced. This directly entails that evidence—more broadly, arguments and testimony—convincing to you need not convince others: they may come into the discussion with very different prior experiences. Hence, given different priors, there is an opportunity for rational disagreement: two people, faced with the same evidence, may come to different conclusions without either acting irrationally.
Second, given identical priors, rational observers will likewise come to identical conclusions. Somewhat surprisingly, this is even the case if they observe different evidence—as long as they are permitted a free exchange of information, and are each aware of the other’s rationality and honesty. This is the content of Aumann’s agreement theorem: rational actors having common knowledge of each other’s beliefs can’t rationally agree to disagree.
René Descartes and the Spectre of Doubt
Bayes’ theorem saw the light of day as a critique of Hume’s skepticism towards miracles. Hume’s own position was that of empiricism—he believed that ‘causes and effects are discoverable not by reason, but by experience’: if we want to know what’s what in the world, it doesn’t suffice to reflect on it from the armchair; our ideas need to be informed by—indeed, grounded in—concrete sense experience. Bayes’ theorem, of course, is nothing but a precise formulation of exactly how experience should shape our beliefs.

The position contrary to Hume’s empiricism is that of rationalism, and its most famous champion was, a century before the time of Thomas Bayes, René Descartes. Descartes believed that certainty about ‘eternal’ truths, at least, could be achieved by a sufficiently skilled intellect through nothing but quiet contemplation. To achieve this certainty, he proposed to strip away everything that was at all susceptible to doubt. The sun rising in the east might just be a hallucination; my memory of just having eaten a chocolate cookie might be mere confabulation; and so on. He conjured up the memorable image of a deceiving demon—an ‘evil genius not less powerful than deceitful’ (with ‘genius’ here meaning something more like ‘spirit’ than ‘intelligence’)—that has ‘employed all his energies in order to deceive’ us.
Bayes’ theorem can then be seen as a hybrid offspring of two in principle opposed progenitors: it tempers a priori commitments—ideas which we may have arrived at using reason alone—in the form of prior probability assignments, using empirical evidence. Aumann’s agreement theorem then entails that if our a priori investigations, our Cartesian rationalist enquiries into that which cannot be doubted, lead us to the same conclusions—and hence, to the same prior probability assignments—, we stand eventually to reach the same judgments on our hypotheses about the world—that is, will be led to the same posterior probability assignments. The conjunction of rationalism and empiricism encapsulated in Bayes’ theorem thus seems poised to yield, eventually, a shared, mutual understanding of the world.
This is, of course, an idealized picture. We are not Bayesian ideal reasoners, and our ability to engage in Cartesian hyperbolic doubt may be questioned. But still, this seems to be an ideal worth aspiring to: we may never reach it, but steadily close the gap, so to speak.
But a deeper worry looms: a single misplaced certainty may serve to spoil this picture of a convergence of ideas. To see why, consider setting the likelihood that you have been given jar B to 100%—say, your mother told you so, and mother is always right. Then, no amount of evidence suffices to nudge your conviction: the probability that you have been given jar A starts out at 0, and remains there, all evidence to the contrary notwithstanding. Thus, our certainties can never be overcome; should we thus err in them, this error admits no means of correction.
Oliver Cromwell and an Appeal to the Faith
A few years after Descartes was aiming to perfect the method of doubt, on the other side of the English Channel, a certainty had emerged: the Scots had chosen Charles II, son of the deposed King Charles I, to be their new king. The English regarded this action as hostile, prompting Oliver Cromwell to march north with the English army—eventually leading to the Third English Civil War in 1651.
Prior to the start of hostilities, in a famous letter, Cromwell appealed to the synod of the Church of Scotland to reevaluate their position—‘I beseech you, in the bowels of Christ, think it possible that you may be mistaken’. Note that this is not an injunction to change their opinion, but simply to change the certainty with which this opinion is held: to be open to the possibility of being mistaken.
This is the origin of what the statistician Dennis Lindley has christened Cromwell’s Rule: to never ascribe a credence of 100% or 0% to any position (unless, perhaps, it is true or false as a matter of simple logic, such as 1 + 1 = 2). The importance of this principle is often underestimated—but it may make the difference between the possibility of coming to a shared understanding, and being locked into distinct communities of opinion with irreconcilable views and no possibility of ever reaching mutual agreement.
To illustrate this, we must slightly amend our earlier example. Suppose there is a jar X, which contains only chocolate cookies—that is, the probability of drawing a chocolate cookie from jar X is 100%. Continuous drawing of chocolate cookies should thus convince every rational agent that they’ve been presented with jar X. If we start with an even assignment of credence to either of the three jars, that is exactly what we observe.
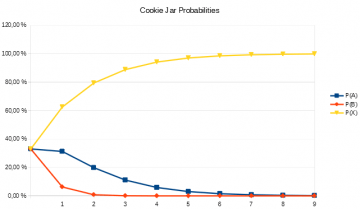
The hypothesis that we have jar B (which, recall, has a probability for drawing chocolate cookies of 10%) is quickly discarded, while that of having jar A has some significant credence assigned to it even after a few cookie draws. However, we will quickly converge to accepting the hypothesis that we’ve been drawing cookies from jar X.
Even if we start out with the suspicion that an all-chocolate cookie jar is a bit too good to be true, thus assigning low credence to it (1% in the example), we will relatively quickly become convinced of our good fortune.
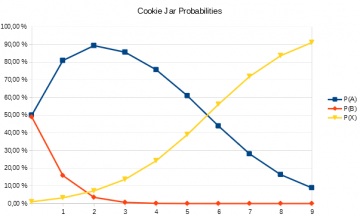
While initially, we find our hypothesis that we have jar A confirmed, owing to the fact that we assigned it a higher credence to start with, as we continue drawing chocolate cookies, we find that we’re forced to accept the reality of the near-mythical jar X.
This shows, incidentally, that even with quite widely different priors, upon being presented with sufficient evidence, an agreement will eventually be reached—although when this happens depends on our initial convictions. Empiricism serves as a check on initial rationalist commitments, and may in the long run overthrow them—although we need to keep in mind that evidence that suffices to convince you may not convince another, without either of you failing to act rationally.
But things are radically different once we stipulate that an all-chocolate cookie jar is an impossibility, and assign it zero credence. Then, due to the nature of Bayesian updating, no evidence whatsoever suffices to overthrow our initial assumption.
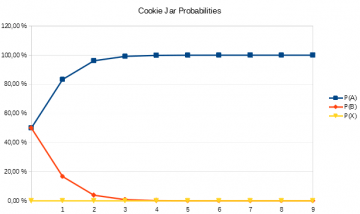
Indeed, matters are worse yet: the same evidence as collected in the earlier two ‘experiments’ is now taken to support a different hypothesis—namely, that of drawing from jar A! Having excluded jar X, each further chocolate cookie will—quite rationally!—support the hypothesis that we’re drawing from jar A, rather than jar B. The blind spot incurred by excluding the possibility of jar X leads us to confidently accept a false hypothesis, and makes a convergence of opinion impossible.
We can think of this as separating the population into two distinct subgroups, which hold irreconcilable convictions: one with initially heterogeneous assumptions about the distribution of cookie jars, which converges to a shared understanding; and one which, due to the exclusion of one possibility, arrives at a quite different conclusion. Between the two, no possibility of mutual understanding exists: there is no means available to the members of the first group to convince those of the second of their mistake. Failure to heed Cromwell’s Rule thus leads to the fragmentation of society along fixed and immovable lines of irreconcilable positions, across which no effective means of communication can exist.
With this in mind, we should strive to always leave a little space for doubt, even with respect to our most cherished convictions. Always spare some room for the possibility of a demon—who, far from being a malignant spirit, in this way turns out to be our most invaluable tool to open up the possibility for genuine appreciation of each other’s views, and for eventually reaching unity across the lines of division that run through modern society.
We often strive to unite under a common cause, using our allegiance to some set of values to stratify society in those who are with or against us. But unity and a healthy discourse can be achieved only through the acceptance—the welcoming—of doubt and dissent, rather than by attempting to quell it, sweeping our in-groups clean of those we feel insufficiently aligned with the cause.
