by Jochen Szangolies
J Richard Gott and the Fall of the Berlin Wall

J Richard Gott, now an astrophysicist famous for the notion that the universe might have created itself by reaching back through time, visited the Berlin Wall in 1969, while an undergraduate at Harvard. There, he made the following prediction (paraphrased):
The Wall will stand for at least 2 and 2/3 years more, but no longer than 24 years.
On November 9, 1989, a rough twenty years later, his prediction came to fruition, and the Wall came down, precipitating the reunification of East and West Germany.
How did Gott arrive at this prediction? Did he have some special insight into the sociopolitical climate of the times? Was he so convinced of the inherent flaws of Soviet communist ideology that he could confidently predict its downfall? Or did he merely note a structural weakness in the construction itself?
The answer is, of course: none of the above. For his prediction, Gott needed only one single point of data: how long the Wall has stood so far. At the time of his visit, the Wall had existed for about eight years—construction having begun on August 13, 1961, two months after GDR council chairman Walter Ulbricht’s emphatic declaration that ‘nobody has the intention of building a wall’ (“Niemand hat die Absicht, eine Mauer zu errichten”).
Armed with this knowledge, Gott estimated that the Wall would stand between one third and three times that time longer. For this, he needed to appeal to two further assumptions—the Copernican Principle, and the Principle of Indifference.

The Copernican Principle is a lesson in cosmic humility: like it or not, you don’t occupy any privileged position in creation. The Principle of Indifference, by contrast, is a guiding rule for adjudicating between competing hypotheses: absent relevant further evidence, belief in each of a set of possibilities should be equally distributed.
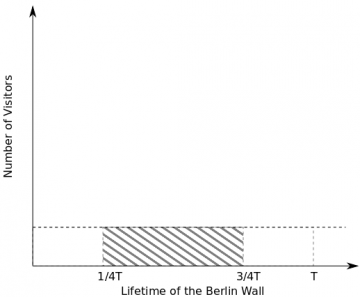
Together, these allow Gott to stipulate that his ‘position’ within the lifetime of the Berlin Wall (the date of his visit) is typical: it essentially corresponds to a random draw from all dates at which it is possible to visit the Berlin Wall—that is, from its total lifetime T. From this, the above conclusion follows almost immediately: half of all visits to the Berlin Wall will occur during half its lifetime. One half of its lifetime lies between a quarter and three-quarters of T. Should you visit the Berlin Wall at the point where one quarter of T has elapsed, it will continue to exist for three times that time; if you visit it when it has stood for three quarters of T, it will continue to stand for one third of that time more.
Consequently, for half of all the visitors to the Berlin Wall, it will be true that it will continue to stand between one-third and three times of the duration it has endured at the time of the visit. Gott’s prediction was, therefore, probabilistic in nature: while it will hold true for half of all those who could make this argument, the other half will end up proven wrong by history. It doesn’t so much establish a matter of fact, as a way to bet, given our knowledge of the situation.
Incidentally, an immediate consequence is that, since the expected future lifetime depends on its duration so far, the greater that period, the longer it is expected to last: old things endure.
Both the Copernican Principle and the Principle of Indifference are assumptions, and thus, may fail to hold. The number of visitors to the Berlin Wall might vary in time—perhaps, as a tourist destination, it might fall out of fashion. Likewise, we might have access to additional knowledge that tells us whether we have arrived at a special point in time during the Wall’s existence—for instance, having just heard Günter Schabowski’s somewhat premature announcement of the opening of the GDR’s borders, expecting the Wall to remain standing for one third to three times its current age would be absurd.
Still, Gott’s technique demonstrates a powerful way of getting lots of information out of very little data. As such, it can easily be generalized to different settings, from the run time of Broadway shows to baseball victories.
However, this style of reasoning had its most famous outing in the ominously titled Doomsday argument: predicting, given the total number of humans that have lived so far, how many humans will exist in total—and, given reasonable estimates on population dynamics, how long our species will endure.
We can reason as above: given the assumption that you’re a typical human being, you should consider yourself to be equally likely to be each of the however many human beings there ever will be (let’s call that number N). Therefore, with 50% probability—as, recall, the claim is necessarily true for 50% of all humans—between one third and three times as many humans as have been born before you, will be born in the future. Consequently, learning ‘your’ number n, like learning the age of the Berlin Wall at the time of visiting, allows you to make an estimate of N.
Estimates for the total number of humans to have lived so far vary, but a rough median number is around 100 billion. That, with the above logic, puts the total number of humans to ever be born, with 50% probability, somewhere between 133 and 400 billion. Given an estimate of the population dynamics over time, we can turn this prediction into a date: as about 140 million people are born per year, we will reach 133 billion cumulative total about 235 years from now; should this rate hold (which it very likely won’t), 400 billion will have lived by about the year 4150.
The precise value of these numbers isn’t too important. The lesson taught by the argument is, rather, the following: the mere fact of our ‘early’ birth makes it unlikely that humanity will continue great lengths of time into the future. As we will see, there are further considerations greatly reinforcing this conclusion.
Of course, likelihood isn’t certainty, and somebody making this argument around the year 1000 would have been badly mistaken in their estimate—but given the assumptions made, the smart bet—the one that ‘pays’ for the greatest number of those that make it—is that the Wall will fall sooner, rather than later.
Enrico Fermi and the Great Silence
Let us now change focus from the Berlin Wall in the 1960s to another Cold War hot spot, the Los Alamos National Laboratory, in the summer of 1950. Here, we meet Enrico Fermi—another physicist with a penchant for drawing quick and accurate conclusions from sparse data. Indeed, such was his reputation that the problems known as ‘Fermi problems’ to this day serve as a gauge for one’s ability to make rough-and-ready estimates based on little information. Thus, when you’re asked to calculate the number of piano tuners in Chicago during your next job interview, and can’t think of an answer, perhaps deflect the examiner’s attention by relating the story of how Enrico Fermi estimated the power of the first atomic bomb explosion by watching pieces of paper float to the ground.
Fermi asked a question that is, in some sense, the opposite of Gott’s: rather than ‘where are we headed?’, he asked ‘where is everybody else?’, thus originating what is now called the ‘Fermi paradox’. ‘Everybody else’, in this question, refers to alien civilizations, and the ‘paradox’ is that we have yet to observe any evidence of their existence.
Admittedly, at first, this seems barely a puzzle, much less a paradox: given the vastness of the cosmos, not having found aliens so far seems like it should hardly be a surprise. But Fermi was keenly aware of something that has heavily impacted on public consciousness in recent times, due to the COVID-19 pandemic: the power of exponential growth.
Going at the speed of our fastest space craft, the Parker Solar Probe, reaching the nearest star would take around 6,500 years. So say that it takes about 10,000 years to reach a new star system, for each system visited so far. Then, the number of visited stars doubles every 10,000 years. There are approximately 300 billion stars in our galaxy. At this pace, it takes a mere 38 doublings, somewhat less than 400,000 years, to get to slightly under 300 billion, and visit every star in the galaxy.
Cosmologically speaking, 400,000 years is barely a blip. Tyrannosaurus Rex and Stegosaurus existed nearly 77 million years apart—thus, any species colonizing the galaxy starting around the time of Stegosaurus would have ample opportunity to engrave ‘Zorblax was here’ on every grain of sand of every beach on every planet orbiting every star in the galaxy before T Rex ever shows up.
It would have taken just one such enterprising civilization, arising a few hundred thousand years before us, to seed the galaxy with life all over. A quarter of all stars, given recent Kepler data, are estimated to harbor Earth-like planets. Yet, looking out into the vastness, we see only void, and listening with giant radiotelescope ears, hear nothing but silence. Where is everybody else?
Cixin Liu and What Lurks Between the Stars
There are multiple answers, of varying degrees of plausibility, for both the Doomsday Argument and Fermi’s question. In both cases, we could just have gotten lucky: some people must be among the first (few billion) to ever be born; some civilization must be the first to ever gaze out into space and marvel at the silence echoing back. Other civilizations may hide from us, or simply not be terribly interested; space travel could be vastly more difficult than we imagine it to be, and simply not worth the risk and resources.
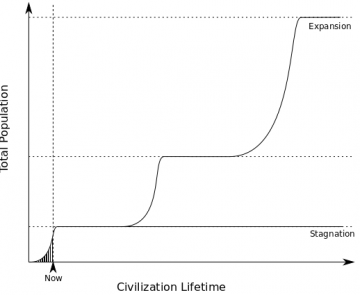
But still. One can hardly help, given the sheer numbers involved, to suspect something else at work. Moreover, the Fermi problem exacerbates the reasoning of the Doomsday Argument. If we ever do take to the stars, the majority of humans—by vast amounts—ought to find themselves within a thriving interstellar community. Only a tiny percentage of all humans, we should expect, are born during the period where humanity is ‘Earth-locked’.
How come we are among them? Moreover, how come we seem to find us at this precise moment in time, just before we are able to make the jump beyond our ancestral home?
The realization that the time in which we live is special breaks the symmetry between us and the rest of humanity—like Günter Schabowski’s announcement of the opening of the GDR’s borders breaks the symmetry between the Berlin Wall visitors. If humanity were to engage in widespread interstellar travel, the chances of you being born right here, right now drop into the minuscule.
Sometime between Fermi searching the skies for alien civilizations, and Gott predicting the ruin of humanity, science fiction writer Cixin Liu is born in a country famous for its own Great Wall—which, incidentally, we should expect to remain standing for 770 to 6900 more years: old things endure. Liu, in his Remembrance of Earth’s Past-trilogy, has popularized an answer to Fermi’s question that doubles as a solution for the puzzle of our special place in the history of humanity: the Dark Forest theory.
Consider that any form of life desires to stay alive. Consider, further, that there is no way to know, a priori, whether another form of life is hostile. Then, the safest—indeed, the only safe—possible option, once becoming aware of another civilization, is to act swiftly and mercilessly, exterminating what must be considered a potential threat. After all, by the same logic, they would have acted in the same way—and thus, they are, in fact, the threat they appear.
In Christopher Nolan’s The Dark Knight, the Joker fits two cruise ships with explosives, giving the passengers of each the trigger to destroy the other. He then threatens that, should none blow up the other, he will blow up both.
This is life in the Dark Forest: each civilization knows that another holds the key to its destruction. The question of why they should act in this way—competition for resources, xenophobia, or sheer manic aggression—is less important than the fact that they could. Moreover, as much as you are suspicious of them, they must be suspicious of you—thus entering into a downward spiral, a ‘chain of suspicion’, that seems like it can only end in annihilation.
Ultimately, this becomes an evolutionary issue: only those civilizations that abide by the laws of the Dark Forest are likely to survive, with those newcomers arriving to the scene, foolishly announcing their presence, finding a swift end. This is, then, why we have so far failed to detect any signs of alien life: those that are there, are hiding, from whatever else is out there, lurking in the void.
But moreover, this also yields an explanation for why we are born in these special times, just before bursting onto the galactic scene, so to speak. In the Dark Forest, most civilizations may reach their peak just before the jump to the stars—just before, that is, they become visible on the galactic stage—and thereby, targets. The typical experience, in the Dark Forest, then is not that of a member of a thriving galactic civilization, but that of being within a few hundred years of developing feasible space travel. The Dark Forest makes an experience like ours from an unlikely outlier into a typical scenario. We are right here, right now, because in the future, we won’t be.
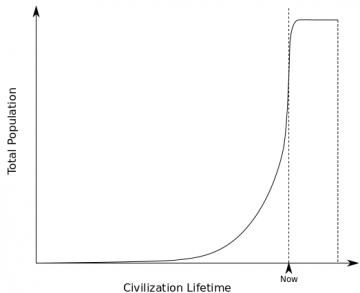
Beyond us, the young civilizations, bursting on the scene, bumbling towards an untimely demise, are then those that have learned the lesson of the Dark Forest—those ever in hiding, ever observant, ever ready to act with maximum prejudice. They are the old ones that have, perhaps, lain vigilant between the stars when Stegosaurus roamed the Earth; they are the ones that will be left, when nothing remains of us but the ghosts of our radio signals echoing faintly within the void. Old things endure, and we are very young.
Then again, that might be too pessimistic a conclusion. In The Dark Knight, the Joker’s plans are foiled when neither ship decides to pull the trigger. Or, we might simply be the lucky ones: in the history of every pan-galactic empire, there’s a tiny percentage of its total population born before its great expansion to the stars. Of those, one might have written an essay such as this one—and been, happily, proven wrong by history.
