by Jonathan Kujawa
For mathematics, 1666 was the Annus Mirabilis (“wonderous year”). For the rest of humanity, it was pretty terrible. The plague once again burnt across Europe [1]. Cambridge University closed its doors and Issac Newton moved home.
Although only twenty-three years old, Newton was pretty well caught up to the state of the art in math and physics. Newton was brilliant, of course, but it also wasn’t so hard for an educated person to be at the cutting edge. After all, it was only thirty years earlier that Descartes and Fermat had introduced the notion of using letters (like x and y) for unknowns and had the insight that by plotting points on the xy-plane you could view algebra and geometry as two sides of the same coin.
With nothing better to do while quarantined at the family home, Newton settled back into the study of math and physics and, it turns out, ignited several world-changing revolutions in the process. Newton cracked open a 1000 page notebook he had inherited from his stepfather and got to work, recording his thoughts as he went. After reading Euclid’s Elements (still the gold standard after nearly 2,000 years!), Descartes, and the other books he had on hand, Newton began posing ever harder questions for himself which he then solved, inventing new math along the way.
Amazingly, Newton’s notebook (which he called his “Waste Book”) still exists! It is kept by the Cambridge University library along with thousands of pages of his other writings. In fact, you can read it for yourself online at the University’s website.
Some of the questions Newton posed could be considered standard, even for his day: computing roots, solving problems in geometry, and the like. Others are more open-ended: “If a Staffe bee bended to find the crooked line which it resembles.” or “To find such lines whose areas length or centers of gravity may bee found.”
In due course, Newton asks himself questions we recognize as the forerunners of calculus.
For example, he challenges himself to compute the area under a hyperbola. Nowadays this is a standard question in the first month of integral calculus. We ask students to compute the area under y=1/(1+x) where, say, x goes from x=0 to x=1. That is, we ask them to compute:
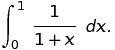
If you remember your calculus, you can check that this integral comes out to ln(2) ≈0.693147…
If you really remember your calculus, you’ll remember the early days of integral calc where you are asked to do calculations using Riemann sums (or, as my students call it, the Hard Way). This is the laborious method where you fill a region with little rectangles, add up their areas, and see what happens as the number of rectangles becomes arbitrarily large. If this rings a bell, then you may recognize what Newton sketched in his Waste Book nearly 400 years ago:
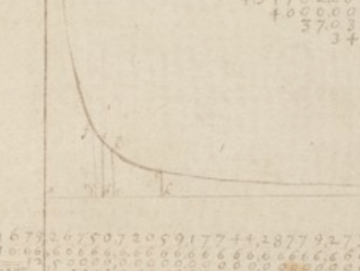
Newton, in fact, did something much more clever than Riemann sums. Something truly astonishing, really.
On the same page as the above picture, Newton explains that 1/(1+x) can be written as 1 – x + x² – x³ + …. That is, you can write it as a polynomial if you don’t mind the fact that your polynomial goes on forever. A twenty-three-year-old Newton just invented power series! I have a clear memory as a college student of feeling like I had made a big breakthrough when I finally understood that the main point of spending half a semester on series was exactly so that we could write functions as power series! What I only grasped through patient explanation by my professor, Newton invented out of whole cloth while sitting at his desk waiting out the plague.
Why is this so amazing? Remember, Newton wanted to compute the integral of 1/(1+x). But integrals of polynomials are easy if you know what calc books like to call the “power rule”. Fortunately, Newton had already invented the power rule earlier in the Waste Book. With it and his infinite polynomial in hand, computing the integral of 1/(1+x) is easy-peasy. Newton used this to calculate the area under the hyperbola out to 55 decimal places!
I told you he had a lot of time on his hands.
Newton describes his technique as a “Method to Square Lines Mechanically” (where “square” here means find the area below). Elsewhere in the Waste Book, Newton answered the question “How to draw tangents to Mechanicall Lines”. That is, how to compute tangent lines (aka derivatives). Newton also understood that integration and differentiation are processes where each undoes the other (aka the Fundamental Theorem of Calculus). Along the way, he tackled all sorts of questions about motion, gravity, optics, geometry, etc. In one notebook over a few short years, Newton single-handedly revolutionized most of physics and mathematics.
Perhaps not surprisingly, recent events turned my mind to Newton’s Annus Mirabilis. My university is closed for the semester; like Newton, the faculty and students have been sent to the country to avoid crowds and pestilence.
Twitter is full of people, perhaps tongue-in-cheek, declaring this their Annus Mirabilis. They imagine all the amazing work they’ll be able to get done without the distractions of the everyday. Academics are especially bad at this (myself included!). We like to think if we weren’t held back by the dullness of our students, administrators, and colleagues, we, too, would be geniuses.
We should be a little kinder to ourselves. These are unprecedented times. It is okay to worry about ourselves, our family, and our friends (including Abbas!). But we can also take a lesson from Newton. Besides his brilliance, Newton’s work depended on having the intellectual space and time to think deeply. We would all be served by turning down the daily noise and taking this as an opportunity for some quietness and deep thought.
Cal Newport wrote a book entitled “Deep Work” on this theme. He argues through data and anecdotes that rich, meaningful, deep work is done in large blocks of concentrated time, devoid of distractions. Dr. Newport also gives suggestions on how to bring more of this time into your work life. Certainly, I find this sort of time essential for thinking about mathematics. I need at least an hour just to get the wheels turning.
“Truth is the offspring of silence and meditation. I keep the subject constantly before me and wait ’til the first dawnings open slowly, by little and little, into a full and clear light.” — Isaac Newton
This is a good time to read good books, start or restart long lost projects, develop new hobbies, write letters, reconnect with old friends, and, yes, do some interesting math :-). If you’d like to read about Newton, I recommend the biography “Issac Newton” by James Gleick. If you’d like an enjoyable take on the ideas of calculus, I suggest you check out Ben Orlin’s new book “Change is the only Constant“.
Of course, Newton didn’t have Twitter, Netflix, or Amazon. He wasn’t deluged every day with the clang and clamor of the nightly news. Nor did he have significant others, children, or much of anyone to worry about besides himself. Nevertheless, we should do what we can to quiet the noise and bring some tranquility into our own lives.
Let us stay safe and, to the extent it can, let this be our own Annus Tranquillum.
[1] The plague hit London no less than six times between 1563 and 1665, killing 10-30% of the population each time. The horror of it is unimaginable.
