by Jonathan Kujawa
In a miracle we neither understand nor deserve, some of the most outlandish inventions of mathematicians’ fevered imaginations have later prove eminently useful in the real world. We’ve talked about some of these here at 3QD. From using the stretchy math of topology to identify data clusters in medicine, to using exotic measures of distance to fill in large amounts of missing data, to using number systems coming from elliptic curves to create strong encryption systems. These are only a few of the gifts we’ve received over the years from mathematics. Several years ago the mathematicians who congregate at mathoverflow compiled a list of applications for each of the main areas of modern mathematics.
Many of these applications contribute billions of dollars of value to our modern world, and yet in nearly every case the mathematics underpinning these were developed years, decades, or even centuries earlier. Bringing a little math to things often pays off bigly.
Plus, doing math is just plain fun! I may be biased, but I say the (fun + value)/cost ratio of math is pretty close to unbeatable. To quote Steve Earle, “I’ll stand on Bob Dylan’s coffee table in my cowboy boots and say that”.
Last month I asserted one explanation for the “unreasonable effectiveness” of mathematics is its insistence on precision in our language and thought. There is a real power in the mere act of mathematization. Even if you can’t solve the problem using actual mathematics, thinking mathematically often lays bare the real questions, the real obstacles, and the possible paths to a solution.
That’s easier said than done. As any calculus student will tell you, one of the most difficult parts of using mathematics on a real-world problem is turning the messy, ambiguous chaos of the real world into something on which you can try to do math.
In a comment to my last essay, Animal Symbolicum rightly pushed back on my call to think more mathematically. As (s)he pointed out, Kant already drew a dividing line between mathematical and non-mathematical inquiries. Words like freedom, ethics, fairness, and love slip and slide when we try to be overly precise. Only a freshman math or philosophy major would try to argue, and with the fervor of the newly converted, that logic and precision are all one ever needs.
Sound bites like “They hate our freedom”, fair trade, income equality, and fake news are all easy to say, easy to agree with, and sound great on the evening news. But, as the essay by Scott Aikin and Robert Talisse at 3QD and the lively discussion which followed shows, it is a challenge to put real meaning to such words.
The flip side is something I call mathiness (to misappropriate Stephen Colbert’s brilliant word). This is the misuse and abuse of mathematics in the real world. There are silly examples where someone devises “The Mathematical Formula for the Perfect X”. For example, in 2010 Geoffrey Beattie devised the supposed formula for a perfect handshake:
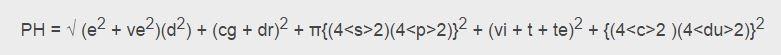
PH stands for Perfect Handshake, of course, and I won’t bother to tell you the rest as it’s all obvious nonsense (I hope!) [1]. The Relatively Prime podcast had an entire episode devoted to this sort of mathiness. For some reason the British media finds such silliness particularly worth publishing. These sorts of things are done in good fun and mostly harmless, although perhaps a little infantilizing to science and math.

More serious is the use of math and numbers to give a false sense of precision. University faculty are reminded of this every term when student evaluations come out. With great seriousness, administrators ponder why on this question you got a 3.8 last semester but a 4.1 this semester. Nevermind that students are marking you on a 5 point scale with little to no guidance on what a 4 should mean. Focusing on such differences is to talk about the noise rather than the signal. But it is easier to use the false precision of numbers to score and compare than it is to do the hard work of meaningful evaluations.
Or think of the 2000 US presidential election recount in Florida. 5,963,110 votes were cast and the final count gave Bush a 532 vote lead over Gore. If you do the math, that difference is less than 0.008% of the total. Plenty of people blamed the votes which went to Nader, but you could just as well point to the 562 votes Harris (of the Socialist Workers Party) received, or the thousands of rejected hanging chads. Indeed, in subsequent recounts, depending on the precise standards used, the election could have gone to either Bush or Gore [2]. There is simply too much noise in the system. The truth is we simply cannot know who won the election in Florida. If we were willing to admit sometimes the messiness of democracy exceeds what we can say mathematically, the Supreme Court would have just flipped a coin.
Economists are particularly bad about using math to give the impression of precision and certainty. Markets and the media swoon when GDP or employment ticks one way or the other by .1%, but the truth is the economy is too big, complicated, and chaotic for us to see more than through a glass, darkly. Nonetheless, policies are made and laws passed based on the promises and predictions of economists. For all their Nobel prizes and mathematical models, the vast majority of econ folks were as blindsided as the rest of us by the Great Recession. In his New York Times column, Paul Krugman explained why he thinks the dismal science missed their chance to be prophets. On the other hand, in November 2016 he also predicted the election of Trump would lead us in short order to another global recession, so perhaps Dr. Krugman shouldn’t cast stones [3]. The other sciences shouldn’t feel too smug, either. As we talked about here at 3QD nearly four years ago, “p-hacking” and the abuse of statistics has led to a reproducibility crisis in science.
Worst of all is when math is used as a cudgel to confuse, trick, and intimidate the unaware and unknowledgeable. The financial industry uses complicated formulas and misleading calculations to steal the hard earned money of people who don’t have a fighting chance. Companies use clever accounting to massage their numbers, boost their earnings, and hide their liabilities. Others hide behind A.I and algorithms to give their policies a veneer of neutrality and fairness. Polluters use margins of error to cast doubt and forestall regulations. Politicians use patently ridiculous revenue predictions to justify their claims tax cuts will pay for themselves.
Good people can disagree on definitions, assumptions, and interpretations, but using math as a weapon is unconscionable. Down with mathiness!
[1] Or go here if you must.
[2] This is Exhibit A of how your definitions and assumptions go a long ways towards determining the outcome. And this ignores all the many shady ways voters are encouraged, discouraged, and prevented from voting!
[3] Although, with trade wars looming, he may well turn out to be right in the end!
