by Jochen Szangolies

The year 2021 marks the 40th anniversary of the introduction of IBM’s first Personal Computer (PC), the IBM 5150. Since then, computers have risen from a novelty to a ubiquitous fixture of modern life, with a transformative impact on nearly all aspects of work and leisure alike.
It is perhaps this ubiquity that prevents us from stopping to ponder the essentially mysterious powers of the computer, the same way a fish might not ponder the nature of the water it is immersed in.
By ‘mysterious powers’, I don’t mean the impressive capabilities modern computers offer, in terms of, say, data storage and manipulation—while it is no doubt remarkable that even consumer grade devices today are able to beat the best human players at chess, and the engineering behind such feats is miraculous, there is nothing mysterious about this ability.
No, what is mysterious is instead the feat of computation itself: a computer is, after all, a physical object; while a computation, say something straightforward like calculating the sum of two numbers, operates on abstract objects. Therefore, the question arises: how does the computer qua physical system connect to abstract objects, like numbers? Does it reach, somehow, into the Platonic realm itself? To the extend that computers can use the result of computations to drive machinery, they seem to present a bridge by which the abstract can have concrete physical effects.
In this ability, computers seem to share one of the key powers of the human mind—to make the abstract causally efficacious, to connect the physical world with the realm of numbers, ideas, calculations—and perhaps, even, thoughts. It is then not surprising that computers are often posited to explain the mysteries of the human mind. The apparent ability of computers to reach beyond the physical and into the abstract gives rise to what one might call the ‘computationalist intuition’: to explain the mind, we need a means to connect the abstract with the physical; computers seem to provide that means; hence, computers seem to be ideally suited to explain the mind.
In this way, we hope, the distinction between brain and mind collapses simply to that between hardware and software, and the presence of thought in the physical world would seem no more mysterious than, say, a calculator’s ability to add two to two and obtain four.
However, I think this gets things fundamentally backwards. For one, we have not yet explained just how computers achieve their mysterious contact with the abstract. In philosophy, this is the question of implementation: what makes it so that this particular hunk of wire and silicon implements that particular computation?
Below, I will make the case that the answer to this question itself depends on the qualities of the human mind: computers, ultimately, are best understood as extensions of the minds of their users (in the ‘extended mind’-sense discussed in the previous column), augmenting them with certain syntactic capabilities (the efficient manipulation of certain tokens, plus storage and recall), but inheriting their apparent semantic qualities from the user’s mind. Ultimately, it is the user’s mind that interprets the symbolic tokens manipulated by computers as pertaining to certain abstract, computational objects (numbers, for example), and thus, ‘nails down’ which computation is actually performed. Rather than appeal to computation to explain the mind, then, we must appeal to the mind to explain computation.
Preliminaries on Computation
To many, this will be a surprising claim. Typically, our experience with computers is that we set a problem or task to them, put them to work, and are presented with a solution—the computation, it seems, is carried out wholly within whatever device was used, without any involvement of the user’s mind.
Computation, in the way we’ll be thinking about it, starts with an input, and ultimately produces some output. A first inkling of the mind’s involvement comes from observing that there is some arbitrariness in deciding just what to count as input and output. In a world without mind, we just have a causal chain of events, which at some point involves, say, the flicking of some switches on a device, and at another, the flashing of some lights in result. These lights will, typically, trigger some further activity in turn, in a manner completely describable in terms of physical causality (the light could fall on a sensor, which triggers an actuator, which…).
But that the switch-flicking and light-flashing constitutes the boundaries of some discrete process known as ‘computation’ is not immediately obvious in this description. Consequently, the delineation of the computing system is within the purview of the interpreting mind, which circumscribes its boundaries to qualify inputs and outputs. Neither is, in itself, privileged; they are merely elements of a longer causal chain, in which they do not play an immediately distinguished role.
All computation can be brought under a common framework. This is a result of what’s known as ‘computational universality’: as demonstrated by English mathematician Alan Turing in his landmark paper ‘On Computable Numbers, with an Application to the Entscheidungsproblem’, it is possible for a single device—a universal computer—to compute everything that can be computed at all. Thus, ultimately, price-tag notwithstanding, the iPhone can’t do anything an Android device is incapable of—in theory, at least (although it needs to be noted that a truly universal device needs an unlimited amount of memory to work with, which will be prohibitively costly on any platform).
For our purposes, this means that we can fix a single language to describe computation. Many choices exist, but for convenience, we can choose functions taking a list (which may be empty) of natural numbers as input, producing a single-number output. In general, for technical reasons, we must admit that these functions sometimes don’t produce any output: this is because there are certain computations that loop forever, and never halt.
Any other computation can be translated into this framework. This shouldn’t be surprising: after all, we know that computers manipulate strings of bits—zeros and ones—and ultimately produce bit-string outputs. But any bit-string can be translated into a number.
This will suffice for our purposes. The key take-away is that whatever we conclude on the basis of computation as realized via natural numbers, due to universality, holds for computation in general.
A Parable on Computational Implementation
Alice, in the course of her daily duties at work, frequently finds herself having to carry out the same repetitive task of tallying up long lists of numbers. Being a tinkering sort, she figures that there ought to be a way to offload at least some part of this repetition to an automated system.
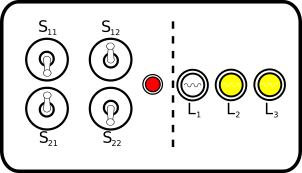
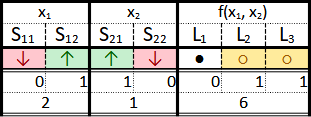
To this end, she starts constructing a simple proof-of-concept device, designed to take two numbers between 0 and 3 and add them together. The numbers are programmed into the device in binary; each number is represented by two switches, which can be either ‘up’ (↑) or ‘down’ (↓). Once the numbers are input, a button starts the computation. The output is indicated by means of three lamps, which can be either ‘bright’ (○) or ‘dark’ (●).
Each configuration of the box can thus be indicated by giving the states of the switches and lamps. The switches are numbered S11 to S22, the lamps are L1 to L3. With this, the complete set of possible states of the device are given in Fig. 2.
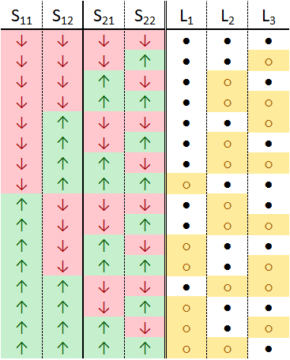
Physically, this gives a full account of the behavior of Alice’s box in every circumstance, limited to the degrees of freedom—switch- and lamp-states—of interest to us. In this limitation, in fact, we see another element of the influence of the user’s mind: every such box, just as every macroscopic physical system, is, of course, composed of a great many more degrees of freedom; to single out just a subset, and consider those as relevant to the computation performed, is an act of arbitrary choice.
Alice now intends to use the box as a means of implementing her chosen computation. For this, she groups the switches into sets of two, and interprets each switch such that its ‘down’-position represents 0, and its ‘up’ position 1. Likewise, she considers an ‘off’ lamp to represent 0, while an ‘on’ lamp indicates 1. Each set of two switches thus represents a two-digit binary number, while the three lamps represent three binary digits.
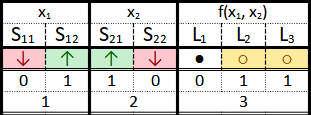
With this choice, it is clear that her aim is fulfilled: computing the sum of 1 and 2 involves setting the switches such that they encode 01 and 10, that is, flipping both S12 and S21 into the ‘up’ position, while leaving the other two ‘down’. After pushing the ‘go’-button, lamps L2 and L3 will come on, correctly indicating 011 = 3 (see Fig. 4).
Satisfied with the day’s progress, she packs up her things, and leaves for home.
Bob, Alice’s coworker, who has always had a bit of a nosy streak, has grown increasingly intrigued by Alice’s toilings. Thus, after Alice left, he strolls over to her desk, to examine her curious contraption. He starts flipping switches, and pushing the button, observing the lights coming on in response, randomly, at first, then systematically, eventually exhausting all possible combinations. He thinks for a while, then makes some notes and, satisfied that he has solved the puzzle, leaves for the day.
The next day, Bob gets to work early, and impatiently waits for Alice to arrive. As soon as she does, he strolls over to her, a slightly smug grin lifting the corners of his mouth. Alice looks up from her work, and stifles a sigh. That specific sort of grin Bob was sporting rarely meant anything good. “Hi, Bob. Can I help you with something?”
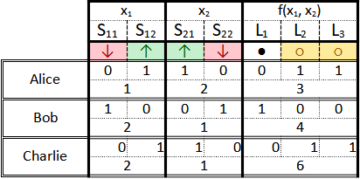
“I figured out your device, you know. It was easy…” He pauses, entreating her to respond, but Alice only raises her eyebrows. After a moment, Bob continues. “See, if you set it like this,” he says, while flipping S12 and S21 up, “and then push the red button, these two lamps come on. The switches encode the numbers 10 = 2 and 01 = 1, while the lamps show 100 = 4…” he trails off, discouraged by the triumphant expression on Alice’s face (see Fig. 5).
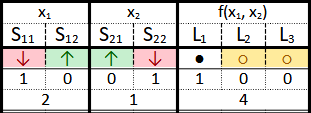
“Sorry, Bob,” Alice interjects, “but that’s not quite it. See, you take ‘down’ to mean 1, and ‘up’ to mean 0, and also, ‘dark’ to mean 1, ‘bright’ to indicate 0. But that’s the wrong way round—your input, in fact, translates to 01 = 1 and 10 = 2, which yields 011 = 3 as an answer.”
Bob’s brow contorts in puzzlement. He’d been so sure… Yet, he could see the logic in Alice’s explanation. “But wait,” he interrupts, “why is your way of assigning numbers to switch positions better than mine?”
“Well…” Alice thinks for a minute. “Because I build it, so what I say goes?”
But Bob can hear the doubt in her voice. “Tell you what”, he continues, “let’s put the matter to Charlie. They’ll know which of us is right.”
Charlie was the head of engineering, and widely respected for their sharp intelligence and technical acumen. However, Charlie was also always busy; thus, Bob delivers the box, together with a written note tabulating the function each of them considers the box to compute and a note asking them to decide which one is correct, to Charlie’s office.
Finally, with a satisfying ka-chunk, the tube containing Charlie’s verdict arrives. However, rather than siding with either Alice or Bob, Charlie has given yet another answer, leaving Alice and Bob puzzled (see Fig. 6).
Eventually, Alice pipes up. “Ah, I think I got it. See, where I interpreted ‘up’ as 1 and ‘down’ as 0, you inverted this assignment; thus, a switch position indicating 01 = 1 for me is 10 = 2 for you. But Charlie inverted the significance of the bits—he considers the rightmost bit to indicate the highest value. So a lamp state ‘off’, ‘on’, ‘on’ means 011 = 3 for me, 100 = 4 for you, and 110 = 6 for Charlie.
Hence, if the device shows ‘down’, ‘up’, ‘up’, ‘down’, ‘off’, ‘on’, ‘on’, then to me, that indicates 1, 2, 3, to you, it is 2, 1, 4, while to Charlie, it is 2, 1, 6.” (See Fig. 7)
“Well, that’s no use at all,” Bob scoffs. “Now we have three possibilities for what your wretched device might be doing!”
“Moreover,” ponders Alice, “it’s clear that this isn’t the last of it. We could just switch Charlie’s interpretation, as you did with mine, and arrive at a fourth option; or we could switch just the interpretation of the lamps—after all, just because ‘up’ means 1, there’s no reason not to consider ‘bright’ to mean 0. Indeed, there seems to be no end to the interpretations generated in this way!”
“So then, which of those is it—does the box compute your function? Mine? Or an entirely different one? How is anybody supposed to tell?”
“Perhaps that’s not the right question to ask, Bob. No matter what we think of the box, the fact is that I can use it to compute my sums; you can use it to compute your function; and Charlie for his. So maybe what the box does is not in the box alone—what matters is what it’s used to do, and all usage requires a user. Without user, if the box just tumbled down the stairs and its switches are set randomly, then all it does is light up its lamps, and not compute any particular function at all.”
The Moral of the Story
If the preceding story has fulfilled its aim, it will have made plausible the idea that computation, at least in the case of Alice’s box, is not a mere matter of what a certain device might be doing, but rather, of how this device is used—how it is interpreted. But every computation can be brought into a form resembling Alice’s box, since every computation can be cast in terms of operations on numbers. Hence, the conclusion is a general one.
Thus, what computation a given device performs is only picked out by its user. Computation is a semantic gloss added over and above the mere syntactic functioning of a given device; without this gloss, this interpretation, there simply is no unique answer to the question of what a given system computes. Computation, on such a view, is then not something ‘out there’ in the world; rather, computers are devices extending their user’s minds, with computation proper only happening in the conjunction between device and user. Far from being our potential intellectual competitors, computers offer us a means of expanded engagement with the world.
But if that’s true, then computation simply will not do as an explanation of the mind’s capacities. For interpretation, taking ‘up’ to mean 1 or 0, is itself a mental capacity (what philosophers call intentionality). Any account of the mind in terms of computation must then end up question-begging, as it depends on that very thing it was meant to explain.
There is no fact of the matter regarding what Alice’s box really computes; each of Alice, Bob, and Charlie is equally well justified in their interpretation. They can, after all, use the device to compute each of their functions—that is, input two values as a question, and obtain the answer, which may be entirely unknown to them, as an output. This is exactly the way we use a pocket calculator, with the interpretation being supplied by our knowledge of Arabic numerals.
I do not expect the account, as it stands, to be convincing to computationalist hard-liners. To be sure, there are various ways to try and resist the above conclusion; some of which I intend to address in a future column. For the moment, however, I will be satisfied if the above has at least put the possibility of viewing computation as an extension of the user’s mind onto the table.
(The interested reader may find an Excel-spreadsheet based simulation of Alice’s device here.)
