by Hari Balasubramanian
I’ve spent twenty-five years in a branch of applied mathematics called operations research; I’ve published papers and taught graduate engineering courses on probability, statistics, and optimization. But even with so much exposure to numbers and quantitative reasoning, I’ve never felt comfortable with math. That might sound like false modesty but it’s not: it’s the truth!
It’s been like this for as long as I can remember. In high school, I dreaded questions where different-colored marbles were drawn randomly from opaque jars. Derivatives and integrals in college courses were equally incomprehensible: I did them mechanically, through rote learning, not knowing why they were being calculated or what they meant. These days I am more familiar with notation, but it’s still not easy. Papers in my field are so crowded with sets and subsets, exponents and logarithms, theorems and lemmas, that I tend to give up very quickly.
My academic colleagues, friends, and some of my students, in contrast, seem far more comfortable. They walk through notation like they are reading prose and seem to grasp ideas much faster than I do. This leads to comical situations where I end up nodding sagely in meetings where somebody is explaining an algorithm or an equation, even when I am not getting it. This nodding reflex, I realize, hides certain fears: the fear of accepting to others how little one knows, or the fear of interrupting a conversation with too many naive clarifications.
Mathematica, a recent book by David Bessis (not to be confused with the software of the same name!), spoke directly to my experience. I finally understood why I feel the way I do. Bessis is a mathematician and I was a bit apprehensive about starting the book. But from the very first pages, I was drawn to his engaging and sincere tone. It felt like a conversation. Anyone, especially those who fear math, can draw solace and inspiration from the book. Indeed, the content is so unusual at times – there’s advice on how to remember one’s dreams, visualize the details of a room from a different vantage point (the ceiling, for instance), and discover our latent ability to echolocate – that it can feel quite tangential to its main theme. But that is precisely the point. Mathematics is not what it appears to be.
In Bessis’ view, there are two sides to math. The “official” side is the formalism and complicated notation that dominates textbooks, research papers, and classrooms. The formal language of math is indispensable since it is the best method we have to communicate ideas logically and precisely. But, as Bessis notes, “this artificial language is so inhuman and so incompatible with our usual way of thinking” that many of us throw up our hands in despair and give up.
The “unofficial” side of math – its joyful essence – is what happens in our minds: how we visualize and manipulate geometric representations to understand a problem better; how we might get intrigued by the puzzle-like quality of certain problems and develop intuitions that evolve over weeks, months, and years. This hidden activity of our imagination is where new ideas and breakthroughs come from. The notation we see on paper is only a second-hand (but, again, necessary) version of this creative insight. In Bessis’ view, if we could “see” or “sense” each other’s intuitions and images directly – perhaps there is a virtual reality world that might make this happen in the future – math would be quite exciting:
If the mental actions of mathematicians were visible, research institutes would have glass walls. Passersby would stop to look, as they would at people who are kitesurfing or rock climbing. In high school, mathematics would be more popular than skateboarding.
Bessis illustrates the difference between intuitive math and formal math through simple examples. Early in the book, he asks: Can a straight line intersect a circle at three points? The moment this question registers, you start imagining a circle and a line in your mind’s eye. Then you move the line around this way and that: the line can be a tangent or intersect the circle at two points on its circumference but never three points. The entire process of understanding the problem and figuring out the answer is by visualizing the geometry of the problem. Now try proving this with mathematical notation without images – how much harder that would be!
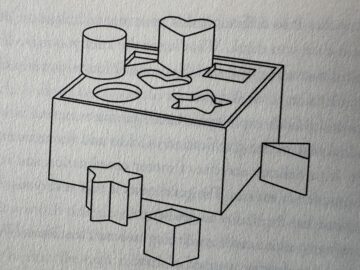A different example is fitting variously shaped blocks into matching depressions on a slab: the kind of puzzle that we all might have encountered as infants. Again, the problem is quite easy once you see it but imagine you had to write a precise algorithm that defines the shapes of the blocks and the depressions. Bessis shows how that is done in the simplest way possible, using language that anyone can understand, but even this description, which spans many pages, is so much harder than understanding it intuitively.
My preference for intuition and aversion to formalism, it turns out, aren’t bugs at all. Surprisingly, even seasoned mathematicians (Bessis included) struggle to read notation-heavy textbooks, and they too rely on mental imagery (at a very different level, of course, like trying to imagine objects in twenty-four dimensions). Alexander Grothendieck, winner of the Fields Medal in 1982 and considered one of the best mathematicians of the 20th century, wrote this:
All my life, I’ve been unable to read a mathematical text, however simple or trivial it may be, unless I am able to give this text a ‘meaning’ in terms of my experience of mathematical things, that is unless the text arouses in me mental images, intuitions that give it life.
§
In his famous book, Thinking Fast and Slow, Daniel Kahneman proposed that there are two ways of thinking: fast, intuitive thinking that comes quickly and naturally to us (which he calls System 1); and slow, deliberate, and intentional thinking that requires much more effort (which he calls System 2). Effortless visualizations of circles and lines, or intuitions that flash into our minds, belong to System 1. Writing a complicated proof with lots of notation or creating new mathematical abstractions is part of System 2. System 1 is quick but not always correct. System 2 is harder but is the basis of logical, rational thinking and therefore better decisions.
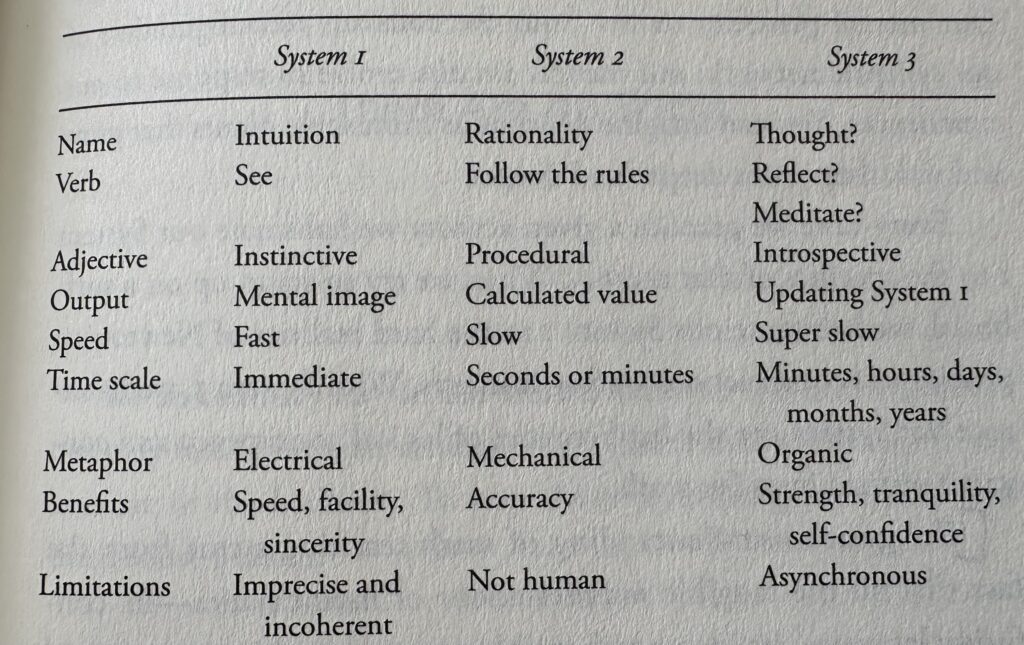
Bessis agrees with Kahneman’s two-systems framework but argues there is more to the story. He proposes System 3: the attempt to reconcile and integrate the often-inaccurate intuitions of System 1 with the rigors of mathematical writing and communication. As you begin to express your vaguely felt intuitions systematically in notation or explain it to someone else, you begin to spot the gaps in your understanding: what Bessis calls “the dissonance between intuition and logic”. Recognizing and clarifying this dissonance corrects and improves your intuition. Your imaginative powers grow, and you gain a deeper perspective of the problem. Your writing becomes more precise. System 3 refers to this iterative dialogue between Systems 1 and 2. There’s a lovely table in which Bessis tries to explain the attributes of the three systems.
This matches with my own experience. Back in the early 2000s, my PhD advisor, John Fowler, introduced me to scheduling problems that came up in the highly controlled clean-room environments of semiconductor manufacturing. These problems involved scheduling “jobs” (batches of integrated circuits) on “machines” (burn-in ovens, photolithography equipment). Each job had its own unique “processing time”, the time needed by a machine to complete the job. Each job also had a “due date”, the time by which had to be delivered. There were cost penalties if a job was completed later than its due date.
The scheduling problem was typically framed like this: How should the jobs be assigned to the machines and in what sequence should the jobs be processed on each machine so that lateness penalties are minimized? Even with, say, 100 jobs and 5 machines, there are a staggering number of possible sequences. The fastest computers today cannot parse through that many sequences to find the best one.
I was quite absorbed by these abstract combinatorial puzzles. I had not liked questions that involved permutations and combinations in high school, but this was different: I had learned to think of scheduling problems visually. I imagined each job as a rectangle with width equal to its processing time (left image in figure below). I would play around with collections of rectangles in my head, swapping them this way and that to see which sequences were better. I would draw them on paper and mull over them to devise new algorithms. All this I preferred to do with minimal notation. Since these algorithms relied on intuition, they were called heuristics. This was very much System 1 thinking: quick and possibly good answers but with no guarantee that they were the best.
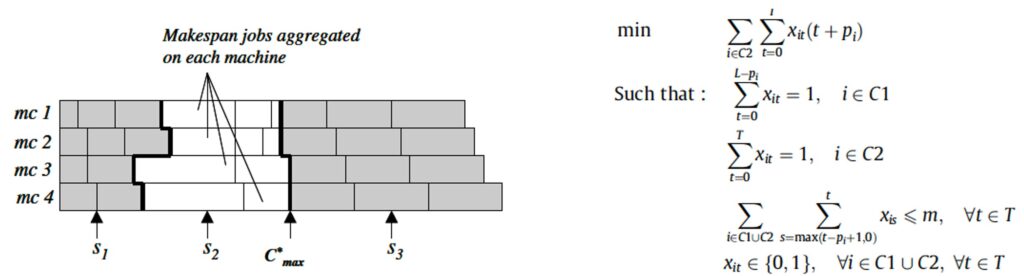
At the same time, through the doctoral courses I was required to take, I learned something called mathematical optimization. Instead of visualizing a scheduling problem, you wrote line after line of equations or inequalities, to precisely and completely describe it (right image in figure above). You fed this logic to a computer to find, using some clever algorithmic techniques, the best possible sequence among billions or trillions of possible candidate sequences. I found this approach quite difficult, even unnatural, but I eventually got the hang of it. Writing the problem mathematically required precision and generality that my visualizations, which always dealt with specific toy examples, could not handle.
All along, without knowing it, I had been using Bessis’ System 3: reconciling my System 1 intuition with the mathematical rigor of System 2.
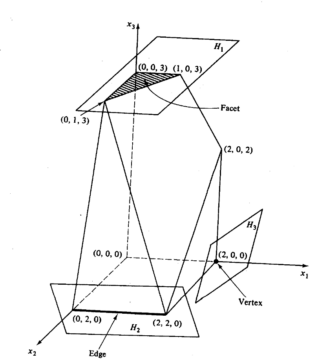When I started teaching a graduate optimization course at UMass, I had a similar bias toward System 1: I avoided writing equations as much as I could. I would show two- or three-dimensional geometric representations on the board (such as this 3-D image of a polyhedron) and try to generalize from these examples. There was a lot of waving of hands as I tried to express the intuition I felt within. I followed the body language of the students closely to gauge whether anything was getting through. However, a pedagogy that relied entirely on System 1 was not sustainable: textbooks and reference materials use a lot of symbols, and there was no way to convey concepts through gestures and geometry alone. I eventually trained myself to write equations on the board. This was much harder than I realized: it’s easy to make mistakes, and you feel vulnerable if the logic does not quite work out. Surprisingly, it was during these moments of uncertainty, when the silence in the classroom felt awkward, that my System 3 thinking kicked into high gear.
The most powerful pedagogical technique for engineering classes is linking math with practical applications. The mood in the classroom shifts, and students begin to emotionally engage with the content. I would classify this under System 3, since an abstract model or concept must be reconciled with nitty-gritty practical details. Students sense where the math works, but equally important, they see where it fails.
§
Bessis emphasizes the tension between intuition and formalism throughout — perhaps too many times. Like many non-fiction books, there’s a lot of repetition and content towards the end is diffuse.
Luckily, there are plenty of vignettes and quirky ideas that keep the pages turning. For instance, Bessis recommends certain sensory exercises to sharpen our mathematical abilities. One example is walking in a room with eyes closed, creating an internal map of one’s movements in relation to where the walls and furniture are. Another is trying to remember the precise details of a place – colors, textures, sounds – from memory. And it’s not always about visual intuition. There’s the remarkable example of Ben Underwood, whose eyes were removed at age two due to retinal cancer but who learned echolocation (the art of navigating by sound) on his own, without any training, by age five. This allowed him to ride a bicycle, skateboard, and play basketball.
There’s also a lot on how dreams can be a conduit for mathematical breakthroughs. The Indian mathematician Srinivasan Ramanujan who learned math without any formal training claimed that “his formulas were correct…because his family’s goddess Namagiri Thayar had revealed them to him in a dream.” Among the more bizarre examples is of Rob Thomasen. Thomason was working on a paper when another mathematician Thomas Trobaugh, who had passed away three months ago, appeared in his dream and told him how to solve a difficult final step of a proof. So insistent was “Tom’s simulacrum” that Thomason listed Trobaugh as a coauthor. (Here’s the full quote.)
Sensory perceptions, the importance of dreams, and other sub-conscious mechanisms: Bessis is trying to reshape our current view of analytical thinking. I found it all quite fascinating. Mathematica has also unexpectedly softened my resistance to formalism. If the goal is to develop intuitions and mental imagery that can creatively absorb you – things that unfold in your mind when talking a walk or clarify themselves unexpectedly in the shower – then perhaps formalism is worth embracing after all.
References
1. Mathematica was originally written in French. Stephen Frey was involved in the English translation. The figure with differently shaped blocks and depressions and the table on attributes of the three systems are photographs I took from the book.
2. The scheduling figure and the accompanying mathematical formulation are from this paper.
3. The 3-D polyhedron image is from the textbook Combinatorial Optimization by Christos Papadimitriou and Kenneth Steiglitz.
Enjoying the content on 3QD? Help keep us going by donating now.