by John Allen Paulos
When studying a technical field there is a strong temptation, especially among those without a scientific background, to apply its findings in areas where they may not make sense or are merely metaphors. (“Merely” is perhaps unnecessarily dismissive since much of our understanding of these fields is metaphorical.) Quantum mechanics and Godel’s theorems are often used (or abused) in this way. Precipitous changes are deemed “quantum jumps” or unusual statements are proclaimed “undecidable.” Not even set theory is immune. I once heard a commentator refer to some curtailment of the first amendment as being inconsistent with the mathematical axiom of choice. Having mocked these pseudoscientific references, I nevertheless, and with a bit of trepidation, would like to briefly explore a metaphorical aspect of chaos theory.
Chaos theory, roughly speaking, studies complex systems of one sort or another whose state or condition changes or evolves over time and are hence termed dynamical systems. The underlying equations or laws describing them are deterministic, but they often give rise to systems very sensitive to initial conditions. (Tiny variations cascading into huge differences.) The systems are also nonlinear, which means that the effects of changes are not directly proportional to their causes. And, trumpets sound here, an astonishing property of nonlinear dynamical systems is that they can exhibit quite unpredictable behaviors that might appear might random, even though subject to deterministic laws.
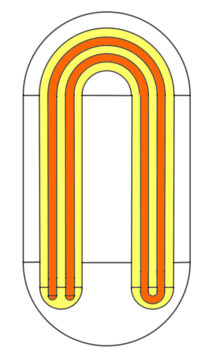
What might such systems tell us not only about weather systems or economic systems, but also about our own inability to predict or make sense of things? An obstacle to predictability is the utter complexity of the associations and linkages in the world and ultimately in our brain. They can be chaotic in both the everyday sense and in the mathematical sense, the description of which I’ll spare you. Regarding the latter sense, the so-called Horseshoe procedure devised by topologist Steve Smale to illustrate the evolution of systems from regularity to mathematical chaos, is most suggestive. Such procedures or mappings are, in fact, a distinguishing feature of chaos.
To understand the procedure, imagine a cubical piece of white clay with a very thin layer of bright red dye running through the middle of it and forming a sort of red dye sandwich. Now stretch and squeeze this cube to twice its length, then fold it smoothly back upon itself to reform the cube. The dye layer is now shaped like a horseshoe. Repeat this stretching, squeezing, and folding a large number of times and you’ll notice that the red dye is soon spread throughout the clay in a most convoluted pattern similar to that in fancy lace or a filigreed pastry. Points in the dye that were close are now distant; other points that were distant are now close. The same is true for points in the clay. It has been argued that all chaos (and the consequent skittish unpredictability, disproportionate responses, and so-called Butterfly effects it gives rise to) results from such stretching, squeezing, and folding in a suitable logical space.
Reading magazines, newspapers, tik-tok, the internet in general, traveling, or simply day-dreaming and free-associating are efficient means for doing to our minds what the stretching, squeezing, and folding does to the original layer of red dye, which might be considered our original view of things. The stretching and squeezing are not physical, of course (despite the occasional similarity of some minds to cubical slabs of clay), but seem related to the way our vision of distant events, disparate cultures, different standards, and the declining salience of personal issues changes over time. The folding corresponds to what we do if we now try to connect the changes in our view of such events, people, and situations to our original previous understandings, which seem to have moved considerably.
Every day, our mental landscape is stretched, squeezed, and, if we allow it, folded back upon itself, and, to reiterate, the effect on us is similar to that on the red dye. Ideas, associations, and beliefs that were close become distant and vice versa, and to touch on a topical issue, it wouldn’t be unreasonable to assume that a faster contemporary rate of stretching, squeezing and folding would lead to a faster onset of chaotic developments, again in both the technical and everyday senses. People keenly attuned to the world and what they read and see are more diffident in their predictions and are themselves are much harder to predict, I suspect, than those whose range and purview are more limited.
This horseshoe metaphor obviously needs development if it is to make any scientific (as opposed to a mathematical) claim and, as stated, is almost unfalsifiable. Still, it is suggestive and seems to be consistent with the idea that certainly (parts of) the world as well as (parts of) ourselves are non-linear dynamical systems vulnerable at times to the same sensitive dependence on initial conditions and chaotic, albeit deterministic, unpredictability as the weather. It does seem, for example, that dark moods or even nervous breakdowns sometimes come over people in the way bad storms bring a sudden end to relaxing walks in the park. Consider also the disproportionate effect of unpredictable, seemingly inconsequential events – the missed planes, serendipitous meetings and odd mistakes that shape and reshape our lives.
A takeaway: Dynamical systems are ubiquitous and complicated, but even a vague, intuitive understanding of their unpredictable behavior and of the effect of so many nonlinearly interacting quantities, sensitively dependent systems, feedbacks and foldings, and so on, should be sufficient to arouse a certain wariness of simplistic pronouncements delivered with overweening confidence.
End of sermon, metaphors, speculation, and horsing around.
***
John Allen Paulos is an emeritus Professor of Mathematics at Temple University and the author of Innumeracy and A Mathematician Reads the Newspaper. These and his other books are available here.
Enjoying the content on 3QD? Help keep us going by donating now.
