by Jochen Szangolies
In the previous column, I wrote about how forces originate from quantum mechanics, using the electric force as an example. Rather than being caused by ‘virtual’ particles being tossed back and forth, which is a picture that seems alluringly intuitive, but ultimately misleads more than it clarifies, a better way is to think in terms of the most characteristic feature of quantum mechanics: interference. Quantum objects, you recall, may appear as particle-like dots upon measurement (say, causing a tiny dark spot on a photographic plate), but are best described in a wave-like manner otherwise. And, while particles can only pile up, waves can both reinforce each other and cancel out, which leads to the familiar pattern of interference.
Interference is most often discussed in terms of the double slit experiment, where, say, electrons are aimed at two narrow, nearby apertures, and, rather than just piling up behind each slit, produce a picture of bands of greater and lesser intensity. But in fact, interference isn’t just important in the quantum realm in the course of clever experiments in which scientists try to get the quanta to identify, once and for all, as wave or particle, only to be frustrated by their refusal. In an often quoted heuristic, suppose what happens if one particle is sent to an aperture with three slits, or four, or five, or more than one aperture: each time, you have to sum the contributions along each possible path to obtain the final intensity at any possible end point of its journey. But once you take that process to the limit, where you have ‘slits everywhere’, at every point in space, you find you can still use that same prescription: sum up the contribution of every possible path, to obtain the intensity (or the probability of finding the particle) at each final point. Thus, we were led to Feynman’s ‘sum over paths’-picture of quantum mechanics.
Now, all that you need to do to find out what happens if you have two electrons is to consider all of the paths both can take, and figure out where they are most likely to go—and there, it turns out that paths that bring them closer together—where each feels a higher potential—preferentially cancel out, while paths that bring them further apart reinforce: the interference pattern shifts each away from the other. Exchange one electron for a (positively charged) positron, and the sign flips, with the likelihood of paths bringing both closer together increasing correspondingly—like charges repel, different charges attract.
But, wait a second—while this gives an (admittedly heuristic) motivation for the existence of electrostatic (Coulomb) forces, we started our investigations, last time, with another phenomenon that has puzzled the greatest minds since antiquity: magnetism! Is the picture developed so far adequate to deal with this mesmerizing phenomenon, too?
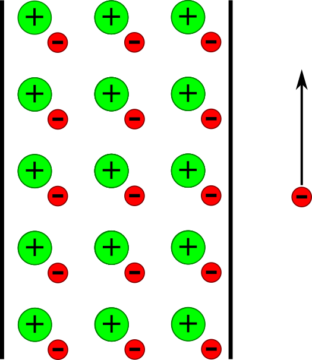Well, in a word, no. Consider the following setting: an electron is put next to a long metal wire. As the wire has neutral charge, the most likely path for the electron to follow is that of a Newtonian body in the absence of a force: it stays where it is, or keeps going at the same speed.
Now suppose we run a current through the wire—that is, we make the electrons in it move. Overall, the wire still remains neutral: hence, the electron should not be affected. But it is! Depending on the direction of the current, it will either be attracted, or repelled. How do we account for that?
The answer, it turns out, depends on that other great revolution of 20th century physics: Albert Einstein’s special theory of relativity. So let’s get a whiff of that before we continue.
What’s So Special About Magnets?
If you know something about special relativity, you probably know it as the theory of weird stuff that happens when you go very fast: astronauts zipping around at near light-speed aging slower than their twins, ladders that seem to both fit and not fit into barns, and the like. What should this have to do with such mundane (if perplexing) objects as magnets, when typical everyday speeds are a billion times slower than light?
But on the other hand: quantum mechanics is often decried as the theory of the very small, and we now know that’s a bit of a fib. While quantum phenomena are typically only observed at very small length scales, due to the necessary precision only being achievable their, they can still be relevant to the explanation of decidedly everyday phenomena. So let’s plod on and see where we end up.
Special relativity arrived on the stage when people were looking for Newton’s absolute space and time, the stage upon which this whole performance plays out, but found that it wouldn’t show up. The Michelson-Morley experiment is to special relativity sort of what the double-slit experiment is to quantum mechanics (and again, it relies on interference!). It tried to nail down the motion of the Earth with respect to the Newtonian background, and found that there wasn’t any—even when the experiment was carried out as the Earth was on opposite sides of the Sun, and thus, moving in opposite directions. So if the Earth might have been, by sheer chance, stationary with respect to the background in Spring, it couldn’t also stand still in Fall!
Just as the double slit experiment seemed to deliver the contradictory verdict that light must be both a particle and a wave, Michelson and Morley’s result seemed to indicate that light must both move with respect to the background (as it moves with the Earth), and not. The result was obtained by sending two beams of light out at a right angle. Suppose the Earth (and with it, the device) moved in the direction of one of the arms of the device: light propagating along this arm should take longer than light traveling along the other arm, and thus, the two beams arrive at the detector in a relatively shifted way—leading to a particular interference pattern.
But no such pattern was observed. This is profoundly puzzling: a car driving on a moving path (say, an enormous treadmill) goes faster when it goes along with, and slower when it moves against the direction of its movement. That seems about as obvious as that things can only ever either be particles or waves!
Well, when you observe an apparent contradiction in your experiment, a good first step is to reexamine your assumptions. But with assumptions as seemingly unassailable as these, this can sometimes be challenging—and indeed, it literally took an Einstein to find the right solution (although, as always, the real history is somewhat more complicated than pithy lines in online articles): no matter how fast you’re going, light always travels at the same speed, at around 300,000 kilometers a second. This, it turns out, has some decidedly strange consequences.
Sailing Against The (Ether-)Wind
Suppose you have a clock of a peculiar kind: it consists of two mirrors between which a flash of light bounces back and forth, and counts one time unit for every round trip. To keep matters simple, let’s say a time unit is just a second—although then it would have to be quite a big clock. However, in a thought experiment, we’re not constrained by the small minds of bureaucratic funding agencies refusing our proposal to build a 150,000 km tall clock, so we can just go right ahead.
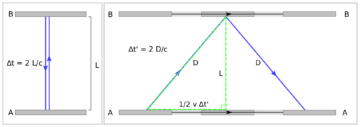
Now take the clock and install it on a movable platform, like, say, a sailboat. A really big sailboat, but, again, funding isn’t a concern. If you’re on the boat, stationary with respect to the clock, the situation is the same as it was on land: that’s the principle of relativity—the same physics obtains independently of the (non-accelerated) motion of your frame of reference. That’s why, on a train, you only notice something when it brakes or picks up speed; its uniform motion at a fixed speed feels no different than when it was standing still at the station. Hence, you observe the clock ticking along, with the light making the trip up and down in one second, just as it did on land.
But now suppose you’re watching the same setup from land, the boat moving relatively to you. The pulse of light, for a sufficiently fast moving boat (the wind is really, really strong that day), will have to cover a larger total distance. But, given the constancy of the speed of light, that entails, from the point of view of an observer on the shore, that the time interval seen as a second for a passenger on the boat must be longer than a second as measured by the stationary clock tower: time must be dilated. Clocks in relative motion to you always run just a tiny bit slower. Given that the velocities involved are, for typical everyday objects, incredibly tiny as compared to the speed of light, you might think that this could hardly have any measurable effects. But actually, it was observed in 1971 using atomic clocks on jet airplanes.
So, moving clocks run slower. That’s perhaps weird, but there’s more: suppose the sailboat, along with its clock, moves a certain distance. You will assign the boat a particular velocity, which is just the length it moves divided by the time it takes it to do so in your frame—i.e. with a clock stationary relative to you. But the clock on the boat will run slower, being in motion, which would lead to a higher velocity—yet any passenger on the boat, for consistency, must see the ocean pass them by with the same speed you assign to the boat as it moves! What gives?
It turns out that the variability of time in moving frames entails a corresponding variability in length: the moving passenger sees length in their direction of movement contracted just so as to account for the otherwise paradoxical discrepancy in velocity.
Now, having gained some first glimpse of the weirdnesses incurred by, well, just having things move relative to one another (who’d have thought!), we can return to our main quarry, magnetism.
What’s In A Wire?
Recall our situation from before: a current flows through a wire. Overall, the wire still contains as many (negatively charged) electrons as there are (positively charged) protons in the atomic nuclei. Yet, the mere fact that these electrons are now moving suddenly leads to an electron moving parallel to the wire being deflected on its path. Wait—things moving relative to one another suddenly behaving weirdly? What was that again about time and length?
Let’s look at a very simplified model of the wire. Basically, there are positive charges—the protons in the atomic nuclei—arranged along a grid, and negative charges flowing around those. For a stationary observer, and so for a stationary electron in particular, there’s nothing that’s changed by the current. But now suppose that the electron is moving relatively to the wire—in particular, relatively to the grid of positively charged nuclei. There are now three parts in relative motion—the electrons in the wire, the electron outside, and the nuclei—so let’s simplify by having the external electron move along with the ones in the wire. Those being thus relatively unmoved, there is no difference to the case of no movement at all.
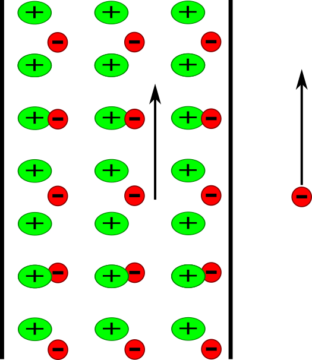
But on the contrary, there is a difference with respect to the nuclei: as those are now moving relatively to the outside electron, the distance between them, as viewed from the moving charge, appears to contract! But that means, now, that per unit volume of the wire, there suddenly are more positive charges than negative ones, the co-moving electrons keeping their distance, so to speak. The wire appears now, for the outside electron, to have a net positive charge! As a result, the charge will now be attracted towards the wire.
Now let’s go back to the original system, in which the wire is at rest, and the charge moves along its length. Clearly, then, we will see the same motion of the charge: and, with no electric field in sight, we must introduce a new quantity to account for this motion—the magnetic field.
Thus, the electric force we got from quantum mechanical interference, if combined with special relativity, yields a magnetic force: fucking magnets, that’s how they work.
Alas, strictly speaking, that’s a little bit of a lie. The story is often told this way: electric field + special relativity = magnetic field. But actually, as we’ve seen in the rest frame of the moving electron, we could just as well have gone the other way around: magnetic field + special relativity = electric field. The only difference is that while we have handy electric monopoles—entities that have only one type of charge—lying around, such things seem to be absent for magnetism, so it was a bit more convenient to proceed in this way. (Incidentally, why there seem to be no magnetic monopoles in the universe is a bit of an open question in physics: one explanation is that the early universe just expanded so quickly that most or all of them got swept beyond the observable universe!)
What’s really going on is that, just as with space and time, special relativity intermediates between electric and magnetic fields—depending on your relative state of motion, you will see one or the other (or a mixture thereof). And, just as space and time, as a result, are unified into spacetime, electric and magnetic phenomena are subsumed in the electromagnetic force.
There is a further wrinkle here that’s less often remarked upon, and that I’ll only briefly touch. Suppose that instead of electricity or magnetism, we start out with the full theory of electromagnetism. As we’ve seen, since special relativity provides the ‘glue’ between both forces, in some sense, that theory must know about its strange effects. And so it does: light, being, as every schoolchild knows today, just an electromagnetic wave, corresponds to a particular solution of the theory—a particular electromagnetic field configuration. From the equations (first written down by the Scottish mathematician and physicist James Clerk Maxwell, and hence generally called ‘Maxwell’s equations’), it is straightforward to calculate the speed at which such a configuration propagates—and it turns out to be the same in every frame of reference! Maxwell’s theory knew about the constancy of the speed of light all along, but it was Einstein who took this hint seriously.
Finally, this also suggests a different way to think about the weirdnesses of special relativity: for ultimately, rods to measure lengths and clocks to measure durations are both described by electromagnetic interactions—the dominant forces that are responsible for the cohesion of everyday objects. But, as the Irish physicist John Steward Bell (him of the theorem) observed in his 1976 article “How to teach Special Relativity”, this gives us a handle of completing the triad, observing that electric field + magnetic field = special relativity: the electric field of a stationary charge is spherically symmetric. But, if that charge is moving, it obtains a magnetic field transversally to its direction of motion, and the electric field is flattened as a result!
But now observe that a rod, of a certain length, is at rest composed of spherically symmetric atoms. Once these are in motion, then, their fields are flattened in the direction of travel—and consequently, the distance between these shrinks. Length contraction is a prediction of electromagnetism! Moreover, electrons orbiting these flattened atoms (flatoms?) now can be shown to do so at a slower pace on elliptical orbits—thus also yielding a consequent dilation of time.
Ultimately, what I hope the above shows is that even everyday objects, such as magnets, contain within themselves a wealth of phenomena usually thought to be far removed from our daily considerations; and that, unraveling these threads, one may arrive at last at a satisfying unity where each strand supports the others as in a self-supporting reciprocal frame structure.