by Jonathan Kujawa
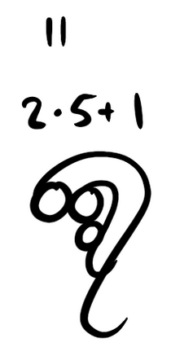
Mathematicians can be extraordinarily fussy about how they write. From having a near fetish on their choice of chalk to Donald Knuth taking 10 years in the middle of writing a multi-volume book series to develop an entirely new typesetting system [1], they spend an inordinate time thinking about how to write something. Indeed, a good choice of notation can be amazingly revealing.
Lately, I’ve become a bit obsessed with something a little more mundane: how we write numbers. The Arabic numeral system of 1, 2, 3, 4, … is so widespread and so ingrained that it is as invisible as the air we breathe. In elementary school, I remember learning the Roman numeral system of I, II, III, IV, …, but only use them occasionally when I need to read a clock or decode the year of a movie or Super Bowl. Certainly, if you asked me to compute
LXIV (CCCXXVIII – XXXVI) + DCCCXXVII
I would have a hard time figuring out that it equals XIXDXV.
Most of us ordinarily work using base ten. This means we use position to record powers of 10 (the tens place, hundreds place, and so on). This also means it is natural to have exactly 10 different symbols. You can have 0 tens, 1 ten, 2 tens, 3 tens, and so on, but 10 tens doesn’t need a symbol since it rolls over and is recorded as 1 hundred. Thus the Arabic system has 0, 1, 2, 3,4, 5, 6, 7, 8, and 9. Their shapes are designed to be easy to draw and read, and are maybe even suggestive of their value. When I was in elementary school, I did calculations by counting the three points of 3, the four corners of 4, and so on.
Altogether, the Arabic number system is efficient, practical, and pretty straightforward. It’s no surprise it became the standard. Roman numerals are terrible to use because they are written in a haphazard way that is disconnected from how we record, use, and calculate numbers. The Arabic system also has the advantage that how we use it to write numbers matches how we read numbers in English. No doubt, the rise of English and the Arabic number system are tied together. I recently saw a funny meme about this:

But it turns out there are lots of other interesting ways to write numbers.
Any computer scientist will tell you you can use bases like binary (0 and 1) or hexadecimal (0 through F) [2]. We talked here at 3QD about the work of Dr. Goins on the numbers are palindromes in various bases. We’ve also talked about how one can use the Exploding Dots notation invented by James Tanton to write numbers in base 2/3 and other such craziness.
But there are ways of writing numbers that go beyond a change of base. Instead of writing numbers in groups of 10 (or groups of 2, 16, or…), we could think about prime factorizations. You might recall that a prime number is one that cannot be factored into smaller whole numbers, like 2, 3, 5, or 12345678910987654321 [3]. Every number can be written in one and only one way as a product of primes (just keep factoring and factoring until you can’t anymore because every number is prime).
The mathematician Richard Schwartz [4] invented a way of drawing numbers as monsters based on their factorization into prime numbers. Each prime number gets its own little monster. Non-prime numbers are turned into a monster by combining the monsters of its prime factors. So the monster for 15 is made out of the baby monsters for 3 and 5.
Dr. Schwartz wrote a children’s book based on his prime factor monsters. It’s a great gift for the budding mathematicians in your family. He even made a downloadable poster of the first 100 number monsters if you’d like a surreal decoration for your home.
What really got me on the typographic kick, though, was the work of Nat Alison. When she isn’t wasting her talents at some fancy startup in Silicon Valley, Nat makes wonderful mathematical creations. One of them is a beautiful calligraphic way of writing numbers. You can draw any number by building up from a swirl for 1, a circle for 2, and rules for expressing powers and multiples. For example, here’s the largest known prime:

The largest known prime is the Mersenne prime 282,589,933-1. To write it in Arabic numbers would require nearly twenty-five million digits and run to 8,000 pages. It is a single elegant image in Nat Notation.
I encourage everyone to check out Nat’s delightful website. She’s made interactive apps for Tetris-like polyominoes, polyhedra, slime mold, and, of course, Nat Notation. If nothing else, bookmark her page for a rainy day. You’ll find all sorts of fun and thought-provoking things therein.
I also recently learned about the Kaktovik Iñupiaq numerals. Like many Inuits, the Alaskan Iñupiat use a base twenty system. This means you use place to count powers of twenty, not ten. When you get to 10 things, you are only halfway to rolling over your counter. Like how binary needs only two symbols and hexadecimal needs sixteen, the Iñupiat system of counting doesn’t fit within the ten symbols of the Arabic system. And just like how we find the Roman numerals unbearably awkward, Arabic numerals are a bad fit for how Iñupiat students think about counting.
So they invented their own! The middle school students in Kaktovik, Alaska in the mid-1990s invented their own system for writing numbers in base twenty. With a mathematician’s eye for both beauty and practicality, the students saw it was important for the numbers to be easy to read and write, easily distinguished from Arabic numbers, and pleasing to look at. Here’s what they came up with:

Like how Arabic numerals match well with English pronunciation, the Kaktovik digits and how they’re put together reflect the lexical structure of the Iñupiaq way of numbering things. Strikingly, student scores on proficiency exams went up dramatically as the new numbering system spread. I’m not surprised. I’ve always found that to master a mathematical concept, I need to find ways to make it my own and fit it within what I already understand.
Once you start looking, you find all sorts of interesting ways to write and think about numbers. The Cistercian monks developed a system for writing any number between 1 and 9,999 as a single glyph. The Mayans also used a base twenty system. We still use base 60, thanks to the Babylonians. English shepherds used base twenty to count their flocks.
An entire book is waiting to be written on the typography, history, and meaning of how we choose to write numbers.
[1] Knuth developed TeX, which soon evolved into LaTeX. Thirty years later, nearly every professional mathematician uses some flavor of TeX on a daily basis.
[2] When poking around looking for stuff on various bases, I found this interesting video by jan Misali. They blew my mind a little bit when they said that every base is base 10 (meaning, if you write 6 in base six, it’s written as 10; if you write 3 in base three, you write 10; etc.). A youtube commentator wrote: “I love how this constantly pings between ‘wow that’s super intuitive and well-thought-out, I can see papers written with these terms’ and ‘I’m pretty sure jan Misali is shitposting right now’.” That about sums it up. Among other things, they are a fierce advocate for base six.
[3] I only learned this year that 12345678910987654321 is a prime, and it immediately became my favorite.
[4] Folks who’ve read 3QD for the past decade might recall that we talked about Dr. Schwartz’s research on the mathematics of billiards here.
