by David J. Lobina
A central property of human thought is the ability to combine two propositions (or thoughts) into complex mental representations, an exemplified by the so-called compound sentences from language, such as the triangle is yellow AND/OR the square is blue, where each clause constitutes a proposition, or thought (the triangle is yellow; the square is blue), and the coordinators “and/or” function as the sentential operators, or connectives, from formal logic (and would be the conjunction connective and or the disjunction connective).
The role of formal logic to examine the ability to represent complex thoughts has been especially fruitful in experimental work on how we represent, and reason with, compound propositions. Indeed, formal logic has informed our understanding of human reasoning since antiquity and remains relevant to modern cognitive science.
Nevertheless, compound sentences often appear to behave in ways that diverge from what is the case in logic. Conjunction and, for instance, can signal much more than a simple union of propositions, which is what logic mandates – e.g., it can mark a temporal, and even causal, relationship between two clauses, as in the bomb exploded and the house was destroyed, which certainly suggests these two events are connected.
The consensus in the literature, however, is that the meaning – the semantics – of compound sentences and coordinators such as and and or is analogous to the meanings logicians assign to compound propositions and connectives in terms of truth tables, with the corollary that the non-logical uses compound sentences exhibit in language use are the result of diverse pragmatic processes (presuppositions, implicatures, etc.).
Thus, the meaning of language’s and corresponds to the truth table of logic’s conjunction, as shown in column 3 of the table below (note the symbols for each connective I shall mention here) – viz., a conjunctive compound sentence is only true when both clauses are true. A similar situation applies to language’s or, though in this case there is usually some ambiguity as to whether the meaning of language’s disjunction is exclusive (an “either/or” reading, as in column 6), or inclusive (it receives “P or Q, or both” interpretation, thus matching the truth table of logic’s inclusive disjunction in column 5).

Curiously, even though that there are a possible 16 binary connectives in formal logic (try to work out why this is the case by paying close attention to the truth table!) and language makes use of a great number of coordinators to link up different clauses (and, because, if…then, etc.), only two coordinators behave like logic’s connectives. That is, of the sixteen possible logical connectives, only two have been unambiguously lexicalised in the world’s languages: the aforementioned conjunction and and disjunction or.
This is not to say that natural languages lack the resources to express or describe the possible state of affairs that the sixteen logical connectives can account for; indeed, the truth tables of the non-verbalised connectives can be derived through the combination of and, or, and negation (e.g., it is not the case that X, etc.), a fact of language as much as of logic.
What’s more, all sixteen truth tables can in fact be derived by the repeated application of one single operator from logic, either the so-called alternative denial connective, also known as NAND or “Sheffer’s stroke” (column 4 in the table), or the so-called joint denial connective, often referred to as “logical NOR” (column 7; not to be confused with the English word nor, though there might be some relation). These connectives have certainly not turned up in any of the world’s languages, and given what they mean, this is perhaps not surprising.
So what do they mean? NAND and NOR are examples of “negative” connectives, as the former is the contrary, or opposite, of conjunction and and the latter of (inclusive) disjunction or, as can be seen on the Table above by contrasting columns 3 and 4, on the one hand, and columns 5 and 7, on the other (the truth tables are reversed, as it were).
But are these unlexicalised connectives (that is, not part of language’s lexicon) “impossible words”? Some concepts do appear to be genuinely impossible to lexicalise – i.e., to become established words of a language, something that is especially true of some verbs – though the concepts themselves seem perfectly entertainable in the beloved language of thought (Lobinas passim ad nauseam).
Take a look at these examples, with the impossible verbs in italics and the putative meanings of such non-existent verbs in parentheses:
He has climbend the tree (‘he has worryingly (for the speaker) climbed the tree’)
He fightaf/runaf (‘he is afraid of fighting/running’)
He didish it (‘he did it shamelessly’)
I sayam you are wrong (‘I am sympathetic in saying you are wrong’)
This doesn’t appear to be the state of affairs for the connectives NAND and NOR, though. These connectives could have been lexicalised in some language had the facts of the matter been conducive to it; thus, if there are no reasons to believe that unlexicalised connectives constitute impossible words, then it ought to be possible to devise an experimental task in which participants would be expected to learn and appropriately comprehend made-up words standing for unverbalised connectives. In other words, if a concept is entertainable, then an invented word meant to embody the meaning of such a concept could be learned in an experiment. And this is what I did with some colleagues!
We used the so-called visual-world paradigm in combination with a behavioural sentence-picture matching task, as described in the Figure below, Panel A (we ran two experiments, for contrast; an experiment with disjunctive sentences, and one with NAND sentences, the latter involving clauses connected by a pseudoword, to which participants were exposed to prior to experimentation).
In this set-up, four quadrants are presented on a screen to participants, with graphic on each quadrant standing as a representation of a possible combination of the two values from each line of a truth table – namely, the combinations TT, TF, FT and FF (columns 1–2 from the Table above) – and thus which combinations would properly apply to the sentences presented to participants – i.e., which graphic would constitute a true statement – would depend on which connective is used to put together the two clauses. In the case of and sentences, only the quadrant representing the TT combination would be the proper target for the sentence, while for NAND, three quadrants would be true: TF, FT, and FF.
So the only thing to do here, first, is to use an eye tracker to follow participants’ eye movements as they listen to the sentences describing the quadrants, which would provide an implicit record of how participants are interpreting the sentences, and then at the end of the experiments, ask the participants to choose which quadrants match the sentences, this time yielding an explicit measure of how the sentences are interpreted.
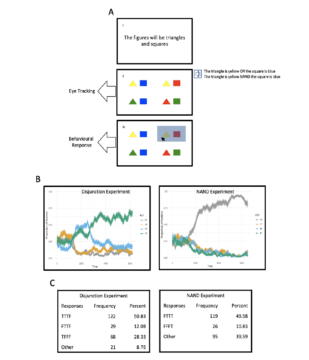
Figure notes: (A) (i) Panel specifies the figures participants see in a trial. (ii) Each quadrant in the experimental panel presents two figures in diverse combinations of colours. An audio of a sentence describing one or more quadrants is played soon after the figures appear, as shown to the right of the panel. Each quadrant represents a combination of the truth values of two propositions (namely, the combinations TT, TF, FT, and FF), while the sentence played to participants is a linguistic representation of two propositions mediated by a logical connective. (iii) At the end of the eye-tracking, the mouse pointer is activated and participants are asked to select all the quadrants that match the sentence. (B) Proportion of fixations to each quadrant (TT, TF, FT, and FF) for a duration of circa 6500 milliseconds. (C) Behavioural responses, where the TTTF pattern, for instance, specifies that participants had selected quadrants TT, TF, and FT.
As described in Panel A, the idea was to track participants’ eye movements as the compound sentences are aurally presented, from the start of the audio file until a few seconds after the audio has finished, at which point participants were asked to select as many quadrants as they thought properly matched the sentence they had just heard.
We predicted that participants would eventually zero in on what might well be regarded as the default meanings of NAND sentences, notwithstanding the fluctuations that were likely to occur during each time-series. Thus, the preferred reading would be the FF interpretation, possibly the core meaning of a connective that is the negation of and, though the mixed forms TF and FT would need to be considered too if NAND sentences are fully understood and indeed interpreted logically. As for the explicit questions at the end, we expected that the most common responses would be TF-FT-FF, in accordance to the truth table of NAND.
The overall data are shown in Panels B-C above. According to the eye-movement record, participants eventually converged on the FF reading from very early on and did not divert from this interpretation. As for the answers, the preferred pattern of response was FTTT for NAND (that is, participants selected TF, FT, and FF), in line with the truth table.
So we won at the predictions game, like every good academic (this stuff will be published in a professional journal one day!). But what does it all mean? The results are noteworthy for a number of reasons, but let’s keep to one here.
The framework offered a compelling way to demonstrate whether participants would be able to conceptualise unverbalised connectives, and in so doing, substantiate the split between the lexicalisation of the logical connectives and the learnability of non-existent words meant to embody the meaning of unlexicalised connectives. Participants showed that they could indeed learn the NAND connective, and moreover, that they interpret non-existent NAND sentences in the same way that they interpret other compound sentences, such as disjunctive sentences. That is, there was a clear preference for what may be regarded as the core meaning of NAND sentences in the eye-movement record, much as is usually the case for other sentences.
This result is of course directly related to the old issue of how language and thought relate, a question as unsettled as any other in the study of cognition. Putting to one side some of the issues the field has been concerned with in relation to this topic – for instance, whether certain thoughts necessitate a specific natural language – our evidence illustrates the long-held claim that linguistic representations do not exhaust what may be in general thought. This point can be traced back to medieval philosophy, but the idea has only received a more rigorous characterisation in modern times.
Apart from Fodor’s language of thought hypothesis, two “principles” are particularly relevant in this case. One is due to John Searle, who once argued in favour of a principle of expressibility, according to which whatever can be meant, or thought, can be said, drawing a connection between what can be entertained in conceptual representations and what can be said in language. This principle is similar in kind to what the American philosopher Jerry Katz called the effability principle: the typical intertranslatibility of whatever content one might be able to entertain, which is based on the apparent fact that whatever thought can be expressed in one language, it can also be expressed in another language in one way or another. Putting these two principles together, it would appear that we must allow for greater flexibility at the side of what can be said than at the side of what can be meant/thought. Or conversely, that the universe of the things we can entertain and think about appears to be greater than the universe of the things we can verbalise and talk about. After all, there are many different ways in which one may wish to linguistically communicate the very same thought, and these different ways will not always reflect conceptual differences.
But enough of this. Next month I will turn to how Kiev has turned into Kyiv, at least in the English-speaking world (and there is a reason for that!).
