by Jonathan Kujawa

At the end of April heartbreaking news spread through my area of mathematics. Georgia Benkart had unexpectedly passed away. I first met Georgia when I was a graduate student, we’d seen each other at numerous conferences and other events, shared a few dinners, and I considered her a friend. Still, I was a little surprised at how much her passing affected me. I wasn’t the only one moved by the sad news. People expressed their sorrow in phone calls, emails, and in social media. The University of Wisconsin — Madison math department collected a sampling of folks’ remembrances on their webpage.
Be what you would seem to be – or, if you’d like it put more simply – never imagine yourself not to be otherwise than what it might appear to others that what you were or might have been was not otherwise than what you had been would have appeared to them to be otherwise. — Lewis Carroll, Alice in Wonderland
Georgia earned her PhD in 1974 and spent her entire career at UW — Madison. She wrote 130+ research papers and still had multiple ongoing projects and collaborations. Her work was remarkable for its breadth, depth, and elegance. Based on her results alone Georgia had a sizeable impact on mathematics. Indeed a recent article in the American Mathematical Society’s main publication was devoted to some of the gems from Georgia’s work. It gets rather technical at times, but I recommend at least skimming through to get the feeling for her research.
I always learn something insightful and new when I read one of her papers. In particular, Georgia always put a high value on clear exposition. It is one thing to figure out how to prove a new result, write down the first ugly proof which can be managed, and call it good. Many (most?) mathematicians would be satisfied. But Georgia always put in the extra work to find the argument which was genuinely illuminating. She has quite a few papers which were of the genre “Oh, that thing you thought you understood and thought was pretty much mined out? Well, actually here is a more insightful way to think about it and look at all the cool things nobody noticed before”.
Likewise, her talks were always well-polished works of art. Georgia had a weakness for wordplay. She’d always deliver the line with a straight face and a twinkle in her eye. She knew what she was saying and she knew you knew it, too. There was no need to make a show of it. Georgia once gave a talk entitled “A Tale of Two Groups” which was a straight math talk interwoven with a series of references to Charles Dickens and his famous tale [1]. A great example of Georgia’s style is the talk she gave as the winner of the Emmy Noether Prize at the 2014 International Congress of Mathematicians in Seoul, South Korea. It is given to someone who has “made fundamental and sustained contributions to the mathematical sciences.” It’s about math research so gets rather technical, but trust me when I say it’s wonderfully accessible to the audience at hand and has its share of math puns.
I no longer remember the real topic of the talk, but it was Georgia who taught me about Charles Dodgson’s condensation method for computing the determinant of a matrix. A matrix is an array of numbers. They are absolutely ubiquitous in mathematics, computer science, physics, data science, and more. The determinant is a single important number computed by an extremely complicated process which is hard to remember and even harder to do correctly. The easiest case is a 2 x 2 matrix:
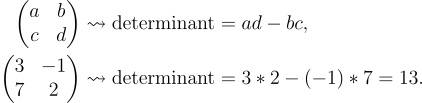
If you take linear algebra, you probably remember the 2 x 2 case. But bigger matrices quickly become a nightmare! The point of the Dodgson condensation method is that you can compute the determinant of huge matrices just by repeatedly using the easy 2 x 2 case! Using the 2 x 2 formula, you keep crunching the matrix down until you finally have a single number, and that’s the determinant you’re looking for. It’s not the fastest method, but it’s a heck of a lot more fun than what’s taught in class [2]!
I can’t recall how, but the Dodgson condensation method played a key role in the results Georgia presented. Sure, you might be able to get to the same place using the messy “standard” formula for determinants, but the elegant approach was to use Dodgson’s method.

Of course, Georgia also had an ulterior motive in telling us about his method. Charles Dodgson is the real name of Lewis Carroll, author of Alice’s Adventures in Wonderland. Like Georgia, Lewis Carroll was a mathematician with a love for wordplay. I can only imagine her delight when she realized his method was just what she needed for her result.
It seems that every month we learn of someone who puts on a kind public face, but is a huge jerk (or worse) in private. Certainly, mathematics has its fair share of Big Shot Mathematicians who don’t hesitate to punch down when it’s convenient. And even the best of us can forget what it was like to be a grad student just starting out.
By all accounts, Georgia was good-humored, kind, and thoughtful to everyone. She frequently worked with young mathematicians — collaborating, giving advice, and generously sharing her time even when she had little to spare. One of my former PhD students, Jieru Zhu, wrote several papers with Georgia after she graduated. I will forever be grateful that she helped Jieru make the transition from student to independent mathematician.

That said, you could tell that Georgia had a steel spine. She was principled and wouldn’t hesitate to speak up when needed. It could hardly be otherwise. In 1992, when Georgia was already a full professor at UW — Madison, there were exactly 5 tenured faculty in the top 10 US math departments. It can’t have always been easy. Regardless of her own experiences, Georgia worked tirelessly behind the scenes to help the mathematical community and, especially, to look out for those who might otherwise not get their fair shot.
As I contemplated writing this essay, I wasn’t quite sure how to explain why losing her affected people so strongly. I’m still not sure I can explain why it affected me so strongly. One thing I realized is that we lost a friend too soon, but we also lost a real guiding light. Georgia was an excellent mathematician, a wonderful teacher and mentor, and was able to do it all with real humanity. I don’t know if it is covid, getting older, or the current state of things, but I find myself with a greater appreciation of the importance of living a full life in all its dimensions.
Georgia Benkart lived such a life and we should strive to do the same.
***
[1] A group is a gadget studied in mathematics which encodes the symmetries of some object.
[2] If it’s so great, why isn’t the Dodgson method taught in linear algebra classes? If while you use it you find that zeros appear, then you have to be rather careful in how you proceed. The “standard” formula will work no matter what, so is less likely to cause confusion. However, it’s so cool that I can’t help but take a day in my classes to tell the students about Dodgson condensation.
