by Jochen Szangolies
At the close of the 20th century, the logical end-point of physics seemed clear: unify all physical phenomena under the umbrella of a single, unique ‘Theory of Everything’ (ToE). Indeed, many were convinced that this goal was well within reach: in his 1980 inaugural lecture Is the end in sight for theoretical physics?, Stephen Hawking, the physicist perhaps most closely associated with the quest for the ToE in the public eye, speculated that this journey might be completed before the turn of the millennium.
More than twenty years after, a ToE has not manifested—and moreover, seems in some ways more distant than ever. Confidence in the erstwhile ‘only game in town’, string/M-theory, has been waning in the face of floundering attempts to make contact with the real world. Without much hope of guidance from experiment, some have even been questioning whether the theory is ‘proper science’ at all—or, conversely, whether it requires a reworking of scientific methodology towards a ‘post-empirical’ framework from the ground up. But in the wake of string theory’s troubles, no other contender has risen up to take center stage.
Suppose, for the moment, things had been different. Some bright young mind, whether working at a university or a patent clerk’s office, comes up with X-theory in 1999, just before the clock runs out on the second millennium. Gradually, through a concerted effort of many researchers across the world, the theory, describing some particular ‘X-entity’, is fleshed out, developed, and clarified—and ultimately, a consensus emerges: from the equations governing the X-entity’s behavior, in the appropriate limits, there emerges both the standard model of particle physics, and the theory of general relativity, Einstein’s celebrated theory of gravity. The ToE is found; physics is solved. We can all go home now and tend our gardens.
But Whence X?
The X-theory is a theory of a particular kind: it takes initially disparate phenomena—general relativity and the standard model of particle physics—and unifies them in a more fundamental setting, namely, the behavior of the X-entities. This style of theorizing has a long pedigree in Western science and philosophy. The pre-Socratic philosopher Thales of Miletus, who lived around 600 BCE, proposed that ultimately, everything is water. Water’s mutability is, after all, readily observable: it transforms to ice and steam, back and forth. Why not into other forms?
Later, in the 5th century BCE, Leucippus and his pupil Democritus developed the theory of atomism—that every phenomenon ultimately can be reduced to the motion of certain most fundamental entities—atoms—in the void. In honor of the centrality of this idea to much of what followed, in science and philosophy alike, I will thus call this style of theorizing ‘atomistic’: a theory is atomistic when it seeks to unify phenomena by reducing them to the behavior of entities at a more fundamental level. Note, however, that I take ‘atomistic’ in a broad sense, here: the unification of electric and magnetic phenomena in the behavior of the electromagnetic field, for instance, is atomistic in this sense.
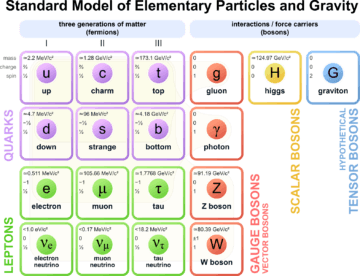
Thus, complex, disparate phenomena are unified by reduction to the (often simpler or ‘more elegant’) behavior of more fundamental entities. The periodic table finds its explanation in the structure of atoms. The ‘particle zoo’ containing more than one hundred hadrons is reduced to different bound states of six quarks. Thus goes the standard ‘success story’ of physics. With the X-entities, we are at the final rung: the dynamics of space and time, leptons and quarks, gluons, photons, W- and Z-bosons, and the Higgs field—all find a natural explanation in X-theory.
But of course, a glaring question remains open: just as we could’ve asked Thales ‘whence water?’, as we could’ve asked the string theorists ‘whence strings?’, for any atomistic X-theory, we will always finally ask: but whence X? Or, as the question was formulated by Hawking in A Brief History of Time: “What is it that breathes fire into the equations and makes a universe for them to describe?”
There seem to be two options. Either, there is some further justification, some theory that accounts for X, for the fire bringing it to life. Then, X-theory wasn’t the ultimate theory after all—but whatever replaces it, if it does so in atomistic style, will be subject to the same question. Or, there is no such justification—Xs and their behavior are just a brute fact about the universe.
But in the latter case, what have we really learned? What does X-theory provide us with beyond a single, perhaps more convenient, framework to describe the phenomena of physics? Certainly: the precursor-theories might have left questions open that can now be answered. Perhaps, by some stroke of luck, there might even be novel predictions amenable to experimental testing.
But has anything really been explained? Previously, we had general relativity, and particle physics, and didn’t really know why; while that question might have been answered, now, we have X, and don’t really know why. One ‘why’ traded for two might seem like progress, but if so, it has now hit a brick wall.
Physics From Elementary Questions
The atomistic method has unquestionably been successful beyond what anyone could reasonably have hoped for. But as we saw, it has its limits—we either find turtles all the way down, or a final turtle standing on nothing, anxious not to look down, lest it should meet the fate of the coyote in so many Road Runner-cartoons.

Perhaps we must think the business of physics differently. The atomistic method takes as an axiom that there is a world out there, whose behavior we can learn by means of experimentation. The experimenter themselves, then, can be abstracted away—the world would be the same, and follow the same laws even if nobody ever discovered them. There would still be X-entities doing X-entity-things, even if they had never, through layers and layers of accident and emergence, given rise to humans thinking about X-entities.
Suppose that instead, we focus on how we obtain knowledge about the world out there—and what kind of knowledge is obtainable. It is not a given that the world comes to us unadulterated—or even, that we can think about the unadulterated world. For example, whenever you try to think about a world without observers, whatever you imagine—a cold, harsh wasteland empty of civilization, or planets careening mindlessly through the void—is already wrong: you can’t help but imagine it from a certain perspective. But if there are no observers, there are no perspectives; a world without observers would be a world unperceived, unimagined.
If thus the concept of ‘world’ presupposes that of ‘observer’, we might start instead by investigating the process by which the observer comes to know the world. Suppose you sit in a windowless room that has as its only means of probing the ‘outside’ a series of buttons. Whenever you push any button, you receive a binary answer—yes/no, true/false, 1/0. Call this an elementary alternative. You’re at leisure to push one, any, or all of the buttons.
This is not such a far-fetched construction. All data from the outside world reach us via neural pathways—and, by von Foerster’s ‘Principle of Undifferentiated Encoding’, signals along these pathways carry no imprint of their origin—they are just ‘trains’ of neuron spikings, which can be translated into featureless binary strings. What can you discover about the ‘world outside’ from this alone?
At first, the answer might seem: not a whole lot. But there’s more than meets the eye. Suppose, for instance, that sometimes, all of the buttons elicit just the answer ‘0’—then, you might conclude that right now, there’s just nothing there, as opposed to the case where at least one produces a ‘1’. So, you can distinguish between ‘nothing’ and ‘something’, ‘object’ and ‘no object’.
But there are also certain regularities that might become apparent. For instance, whenever button 12 yields ‘1’, so does button 73—in fact, there are certain patterns that always go together. This allows you to make predictions, and test them; furthermore, it allows you to distinguish between different ‘somethings’, by means of certain stable patterns. Say one object is identified by the sequence ‘101…’ on the first three buttons, and another by the sequence ‘010…’. Having observed the sequence ‘10’, you can predict that the next button pushed yields ‘1’.
You can discover even more. Suppose that, while there are certain stable patterns, some button-readings vary on occasion. You might not want to create a new category of object for each such variation; rather, you might conclude that objects have certain properties that are immutable or essential, while others are accidental or variable—like an electron that always has the same mass and charge, but whose spin-orientation along a given axis may vary. This introduces probabilities into the picture: observing a pattern characteristic for a given object, you are able to predict that a certain button press yields 1 with probability p, and 0 with probability (1 – p).
Still, the world thus reconstructed is a paltry thing. Everything in it can be represented by a point on the interval between 0 and 1—at the end-points for any essential properties, and somewhere between for those properties that vary. Moreover, new objects just yield new points on that line, and no further essential novelty.
That is, provided the world is classical. A quantum world, investigated in the above way, holds some surprises.
Quantized Elementary Alternatives
The quantum theory of the elementary alternative was formulated by German physicist and philosopher Carl Friedrich von Weizsäcker in a series of papers entitled Komplementarität und Logik (Complementarity and Logic) I-III between 1955 and 1958. Weizsäcker calls the elementary alternative ‘das Ur’ (pronounced more like ‘poor’ than ‘pure’), after the German prefix ur-, denoting something like primitive or primordial (compare: Ursuppe, the primordial soup, or Urknall, the primordial bang, or big bang). Hence, the theory of the elementary alternative is known as ur theory, which doesn’t do its googleability any favors.
Weizsäcker’s starting point thus is basic logic—how we should reason about the things in the world. Complementarity, then, is the central phenomenon of quantum theory that entails the necessity of formulating the description of a system in terms that are both mutually exclusive and jointly necessary (as in wave/particle duality; see the previous discussion here). As Weizsäcker argues, this should be a fundamental building block of the logic used to reason about and construct scientific theories. But this itself constrains the theories that can be built, in surprising and illuminating ways.
Weizsäcker’s outlook is, thus, at first brush broadly Kantian: there are certain concepts that we may consider ‘innate’, that dictate the form of our experience of the world. Kant considered, e. g., space and time to be among these; hence, no non-spatial experience is possible, or even imaginable.
This is a break with the atomist tradition. Rather than simply being at the receiving end of unbiased data emanating from the world, the observer in this picture mediates the data through the process of observation—thus, the sorts of theories that can be built do not describe unvarnished reality, but the experience of an observer in the world. The idea of an observer-less world is immediately nonsensical, as the notion of ‘world’ carries that of the ‘observer’ with it.
From there, Weizsäcker proposes to built a theory of physics, taking as its point of origin nothing but the ur theory, that is, the quantum theory of the elementary alternative—the qubit, in modern parlance. In this way, he proposed an information-theoretic grounding for physics three decades before Wheeler ever coined the famous slogan ‘It from Bit’.
But what does ‘going quantum’ add to the above picture? Quite a lot, it turns out. First of all, in a classical world, repeating questions (pushing buttons already pushed) always yields the same answer, no matter what other buttons have been pushed in the meantime. But in a quantum world, asking certain questions ‘unasks’ others—a consequence of the uncertainy relation, and thus, ultimately, of complementarity: for instance, measuring a particle’s momentum entails a loss of knowledge about its position, and vice versa.
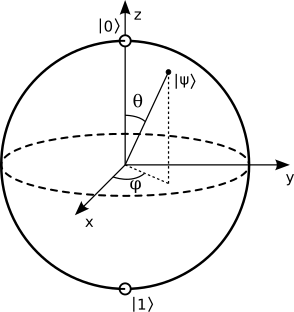
This has the consequence that in quantum mechanics, an elementary alternative can no longer be represented on the one-dimensional line between 0 and 1. Rather, the state of the most simple quantum system—the ur, or qubit—is given by a point on a sphere in three dimensions—the so-called Bloch sphere.
But then, Weizsäcker asked, what does this mean for physics? If every physical object is to be built up from urs, and each ur is transformed by means of a rotation in three dimensions, then in total, no difference should be observable—that is, rotations in three dimensions ought to be a physical symmetry. This is then taken to predict the three-dimensional nature of physical space. Compare string theory: its most direct prediction is that of a nine spatial dimensions—which is quite obviously contradicted by empirical data (just look!), and thus, the excess dimensions have to be swept under the rug by means of just making them really, really small.
Weizsäcker and collaborators have argued that many features of the observable world follow in a similar manner from the theory of urs. An elaboration of the above argumentation yields not only 3D space, but the 4D spacetime of the special theory of relativity—a surprising connection that has reemerged in modern times, and indeed, has been elaborated on in the ‘It from Qubit’-program, which seeks to ultimately derive even the general theory of relativity from elementary quantum information.
Thus, rather than just a collection of points on the interval between 0 and 1, the data our experimenter obtains from a quantum world is more naturally represented in a three-dimensional arena. But things do not stop there. Using a process of ‘multiple quantization’, Weizsäcker and colleagues, such as Michael Drieschner, Holger Lyre, and Thomas Görnitz (the latter of which is probably the most active present day proponent of a version of the theory), have proposed to construct particle- and field-states, thus filling the arena of spacetime with matter. Multiple quantization can essentially be conceived off as applying the logic of complementarity to its own propositions (what is sometimes called the ‘meta-theory’), yielding a stepwise process of emergence of more complex structures.
Nevertheless, ur theory, as it stands, is a very incomplete construction. Indeed, Weizsäcker himself often lamented that he was unable to recruit more of his colleagues to his cause, and felt that this had hurt the theory’s development (one can speculate in how far Weizsäcker’s controversial role in the ‘Uranverein’, the Nazi program to built an atomic bomb, might be connected to the lack of international recognition). But in my eyes, its central attraction is not (at this stage, at least) the completeness of the reconstruction of physics it achieves, but rather, its break with the traditional atomistic mode of theorizing. Ur theory avoids the troubles of atomism because the urs are not just the latest X-entities: they are not entities at all, being elements of knowledge, of our theorizing about the world, much more than ‘stuff’ out there. The ur is a question asked, and the world is (a representation of) the answer received.
Quantum theory—and nothing else, no spurious X-entities—lies at the foundation of the physical world, for Weizsäcker. There remains the justification of quantum theory, which he attempted to give by means of an axiomatic reconstruction. The question of whether these axioms can do the work needed as ‘synthetic a priori’ in Kant’s sense is then a lacuna at the foundation of the theory. Could the world have been classical, instead of quantum?
I have argued in favor of a negative answer to this question—quantum theory is not optional. Rather, the logical structure of theory-building mandates that there is a maximum to the information obtainable about any physical system—an epistemic horizon that delimits our knowledge. From this, key concepts of quantum mechanics can be reconstructed.
This then yields the tantalizing possibility that the final theory of physics is not to be found in the arcane properties of some X-entity, but has been with us all along—in the form of the quantum mechanics of elementary alternatives.
