by Jonathan Kujawa
On Friday before sunrise, I walked across campus with our dog, Lola. Summers in Oklahoma are unpleasantly hot. If you can manage, it is best to be out early. Besides, Lola is an early riser. It is hard to stay in bed when you can hear the pacing of impatient paws.
While crossing campus I stopped to enjoy the view of Venus, Jupiter, Mars, and Saturn sprinkled in a line across the eastern sky. A conjunction of thoughts joined together in my mind. I had a 3QD essay due this weekend, it was Friday the 13th, and it is surprising but true that the 13th of the month is more likely to be on a Friday than any other day.
My former colleague Ralf Schmidt was the one who first told me this startling fact and why it’s true. I thought it would be a pleasant diversion in these turbulent times to talk about something which matters not at all. Why is it that the 13th more often lands on a Friday?
As far as I know, this curiosity was first observed by B. H. Brown at Dartmouth College in the 1930s. In any case, he was the one to pose this as a problem in the American Mathematical Monthly in 1933.
As a first try, we might argue as follows. Each day happens as often as any other, and so they are equally like to occur. That is, if you tell me it is the 13th of the month, since each of the seven days of the week is as likely as another, then there is a 1/7 chance (approximately 14.286%) that it is a Friday.
Coming from a different angle, we could notice that there are twelve 13ths in a year. With this in mind, you might instead argue that 12/7 of the 13ths in a given year will be on a Friday. That is, on average a year will have 1.714 Friday the 13ths.
Coming from a third tack, an ordinary year has 365 days. This comes out to exactly 52 weeks plus 1 day. This means that since the first day of 2021 was a Friday, then there will be exactly 52 Mondays, Tuesdays, Wednesdays, etc., but 53 Fridays. You might think that this means that a 13th is slightly more likely to land on a Friday in 2021. Surely 2021 must have had at least two 13ths, right? Nope. In 2021, August 13th was the only Friday the 13th [1].
All this talk of averages and likelihoods is misleading [2]. These averages and probabilities are fine as far as they go, but they don’t give us the actual, precise answer we’re looking for. After all, the days aren’t randomly sprinkled through the year. As soon as you told me that January 1, 2021 was a Friday, the rest of the calendar was set.
To avoid any mistakes, we should just sit down with a comprehensive set of calendars and tally up all the Fridays the 13th. However, to do an accurate count and to solve Dr. Brown’s puzzle, we need to account for several wrinkles. We’ve already noticed that in an ordinary year one day happens one more time than any other. Worse, every fourth year is a leap year and that year has 366 days. This means we sometimes have to account for 52 weeks plus 2 days. Even worse, some leap years are skipped!
In the modern Western calendar here are the rules:
- If a year is not evenly divisible by 4 (like 2021), then it has 365 days.
- If a year is divisible by 4 (like 2020), then it is a leap year and has 366 days.
- There is an exception to the previous rule: if a year is divisible by 100 (like 2100), then even though it’s divisible by 4, you skip the leap year and only have 365 days.
- There is an exception to the previous exception: if a year is divisible by 400 (like 2000), then even though it’s divisible by 100, you actually do the leap year after all.
Don’t blame me! The problem is that the astronomical year given by the Earth going around the Sun doesn’t quite match the calendar year [3]. Each year the astronomical year is off by a little more than one-quarter of one day. This causes the two calendars to slowly go out of sync. Adding a day every fourth year corrects for this slippage, but it’s a slight overcorrection. So to counter the overcorrection we skip a leap day once every century. But that itself is an overcorrection in the other direction. So we add back a leap day once every 400 years. Yeah, it’s kinda complicated.
If we contemplate these rules, we see that the leap year calendar repeats itself every 400 years. Whatever rule applies to a given year, the same rule will apply 400 years from now [4]. And, moreover, there is a total of 146,097 days in those 400 years. Since 7 divides 146,097 evenly, those 400 years have exactly 20,871 weeks plus 0 extra days. This means that not only does the calendar repeat itself, but so do the days of the week. For example, since January 1, 2021 was a Saturday, it must be that January 1, 2421 will also be a Saturday.
To determine the Fridays the 13th, we should take the calendars for 400 consecutive years and count them up. This is exactly what Raphael Robinson at UC Berkeley did in 1933 to answer Brown’s puzzle. Robinson counted and found that in 400 years there will be 4,800 13ths and the tally of how they land on each day of the week comes out as:
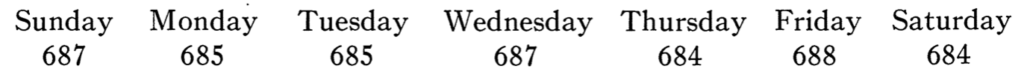As you can see, Friday has more 13ths than any other day of the week!
This doesn’t quite explain things, though [5]. There is a funny pair of coincidences that makes the above imbalance possible. The first is that 7 divides 146,097 evenly. If it didn’t, then since 7 is a prime number, we would need to take 7 x 400 = 2,800 years in order for the days of the week to perfectly sync with the system of leap years. But in that case the tallies would all average out and you’d have the same number of Fridays the 13th for each day [6]. Since 7 does divide 146,097 evenly, Robinson’s tally of 400 years is correct and there is no averaging out.
This is where the next coincide happens. Notice that 4,800 is not evenly divisible by 7. That means it is not possible to evenly divide the Fridays the 13th among the seven days of the week. Somebody has to have more, somebody has to have less.
It’s safe to say that the Gregorian calendar, the system of leap years, and the spooky significance of Friday the 13th isn’t one big conspiracy. In the end it’s all one big cosmic coincidence.
[1] It turns out that every year has at least one Friday the 13th. They can also have two or three Fridays the 13th. Three can happen in a non-leap year if it starts on a Thursday (then February, March, and November will have a Friday the 13th). Three can also happen in a leap year which starts on Sunday (with a Friday the 13th landing in January, April, and July).
[2] If all these arguments sound reasonable to you, then you’re in good company. Probability was one of my worst classes. I always ended up over- or under-counting things. It’s very easy (at least for me!) to calculate a value that sounds good, but doesn’t actually answer the question asked.
[3] Another headache is that days aren’t exactly 24 hours long. There are slight variations in the speed of the Earth’s rotation. To keep clocks in sync we have occasional leap seconds. Worse, the rotation of the Earth is slowing down. Pretty soon a rotation of the Earth will take 25 hours! By soon I mean in a few hundred million years, so maybe don’t bank on that extra hour.
[4] We are optimistically assuming that 400 years from now we’ll still have calendars, leap years, and Fridays the 13th. That might be overly optimistic, but let’s hope for the best!
[5] I once heard a talk by Wilberd Van Der Kallen. After telling us the big result he said “I don’t understand it, I can only prove it.” Knowing something is true is not the same as understanding it. We want to understand it.
[6] Specifically, the first 400-year block would be as Robinson calculated. The next 400-year block would be the same numbers shifted some amount to the right, the third 400-year block would be the same numbers shifted even further to the right, and so on. After 2,800 years each day would have exactly 4,800 Fridays the 13th.