Patrick Honner in Quanta:
If you’ve ever had to buy hot dogs for a cookout, you might have found yourself solving a math problem involving least common multiples. Setting aside the age-old question of why hot dogs usually come in packs of 10 while buns come in packs of eight (you can read what the National Hot Dog and Sausage Council has to say about it here), let’s stick to the math that gets our hot dogs to match our buns. A simple solution is to buy eight packs of hot dogs and 10 packs of buns, but who needs 80 hot dogs? Can you buy fewer packs and still make the numbers match?
Let’s list how many of each item you get by purchasing multiple packs.
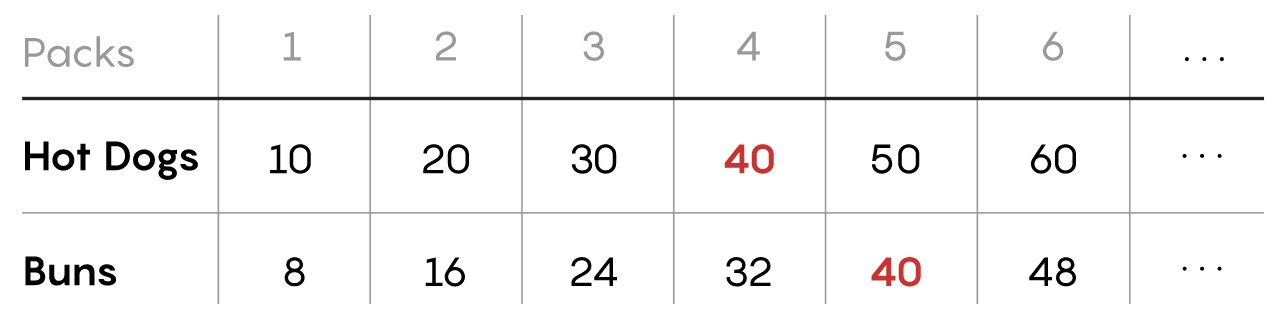
There’s a 40 on each list because 40 is the least common multiple (LCM) of 10 and 8 — it’s the smallest number that is evenly divisible by both numbers. If you buy four packs of hot dogs and five packs of buns, the 40 hot dogs will match up perfectly with the 40 buns.
But what if the hot dogs instead came in packs of five (maybe your friends and family like an artisanal brand that comes in prime-numbered packs), and even 40 is more than you need? Can you do better than the simple solution of buying eight packs of hot dogs and five packs of buns?
More here.