by David Kordahl

If you follow science news, there’s a good chance that you’ve recently heard about Muon g-2 (pronounced “mew-awhn gee minus two”), an experiment whose preliminary results were announced to media fanfare and general excitement. The experiment’s most recent iteration is going on at Fermilab, the physics facility outside Batavia, Illinois, but it continues an experiment that wrapped at Brookhaven National Lab, over in New York, back in the mid-2000s. The experimental appratus, a magnetic ring some 50 feet across, traveled from one lab to the other in a single piece—the pictures of this are impressive—all so the anomalous magnetic dipole moment of the muon could be measured with an unprecedented precision.
The vocabulary itself here was a challenge for headline writers. The main focus was about how this measurement of … whatever it was … would be revolutionary. “A Tiny Particle’s Wobble Could Upend the Known Laws of Physics,” went a headline at the New York Times. “Muon g-2 Experiment at Fermilab Finds Hint of New Particles,” wrote Quanta. An explainer comic from the American Physical Society stressed how “new discoveries are on the horizon,” and Résonaances, a blog widely read by physicists, noted the deluge of new g-2 papers, and found hints that might “open a new experimental era that is almost too beautiful to imagine.”
I have no argument with any of these articles, but they are mainly concerned with narrative building, with explaining how the new measurements fit into an ongoing quest to go beyond the standard model, the “standard model” being a bland summary term for all fundamental physics except for gravity. (Gravity gets its own fundamental theory—viz., general relativity.) But while these articles ably summarized why physicists care about these measurements, they contained hardly any physics, hardly any material of the sort that, after reading, lets you understand what’s going on out there, beyond mere social descriptions.
Then again, you can’t blame journalists for this. Physicists sternly tell journalists that they shouldn’t imagine anything like a little spinning basketball when they talk about a particle’s spin. Spin, physicists will tell you, is a quantum phenomena, quite unlike its classical versions.
Which is fine. But before these physicists were taught about the quantum phenomenology of spin, they first learned how to manipulate simple classical models. And while these classical models ultimately fall short, they give us the language we need to transcend them. To get on the rooftop of the house of physics, it’s helpful to have a ladder, which is what classical physics provides. In a few paragraphs, I hope to sketch a few sturdy ideas that can be kicked away as soon as they’re no longer useful.
As is the custom of physicists, the Fermilab seminar on the ongoing Muon g-2 experiment alternated between basic and advanced material.
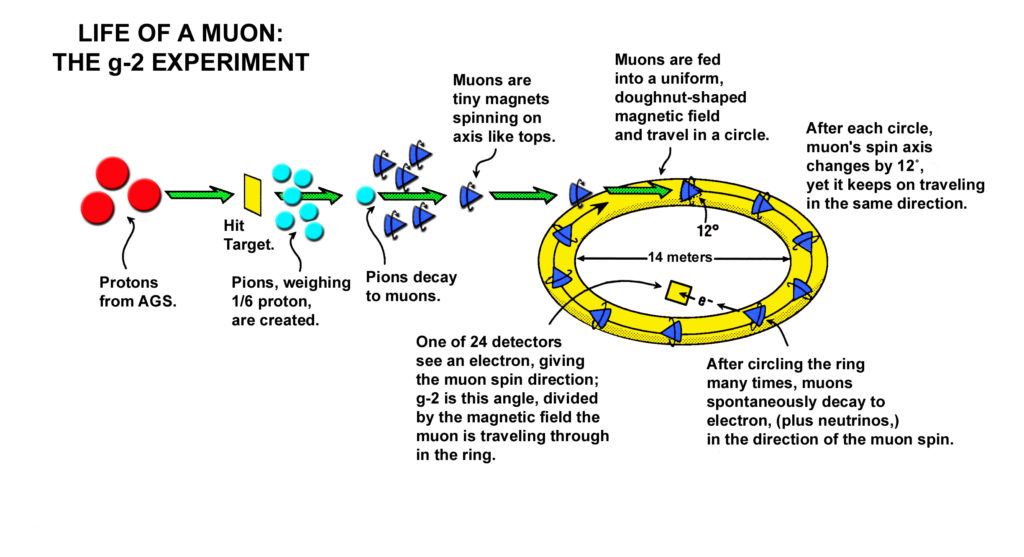
So all right. What about that “anomalous magnetic dipole moment of the muon,” huh? If we can understand those words, that’d be a lot already.
We can start off with the muon. Like the electron, the muon is thought to be an elementary particle. In fact, the standard model’s description of the muon copies everything about the electron exactly, with one major difference: the muon is about 207 times more massive than the electron. This difference in mass allows the muon to decay into lighter particles, including the electron itself. An average muon at rest only hangs around for about a millionth of a second, yet muons are still pretty common in nature. Enough muons are produced when cosmic rays bombard our atmosphere that (to repeat a standard factoid) around one muon will penetrate an outstretched hand each second that it’s outstretched.
But for the moment, let’s forget the differences between an electron and a muon. For the purposes of our slightly wrong picture, they’ll be the same. To help us understand what’s going on with the spin, we can temporarily imagine the muon as a little loop of wire with a current going through it.
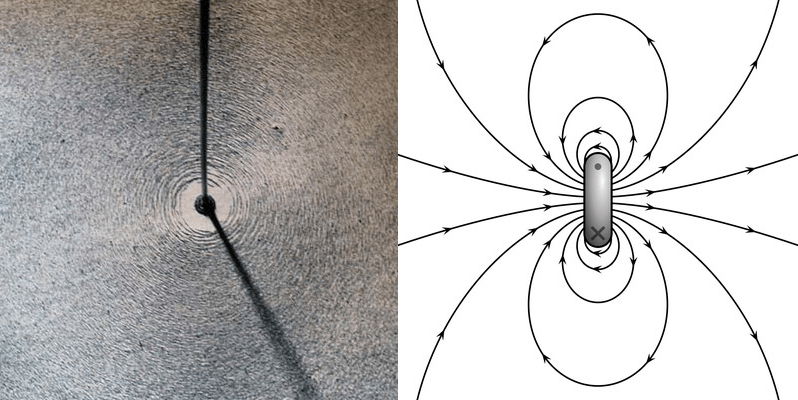
Why this shape in particular? Because magnetic fields are easiest to picture around wires. Take a look at the photo on the left in Fig. 1 below. For a wire with a steady electric current running through it (think literally, here: you could take a long wire and connect its ends to a big battery), sprinkling iron filings around the wire will let you visualize the shape of the magnetic field that has been produced. The magnetic field lines make closed loops around the wire, loops that connect back on themselves.
And how does this relate to the magnetic field of an object like an electron or a muon? That’s where the wire loop comes in. To imagine a magnetic dipole, think about what happens with the magnetic field if we go from the long wire to a short loop. Imagine how the circular magnetic field lines might deform. As in the diagram on the right in Fig. 1, the magnetic field would point out of the loop on one side, and into the loop on the other, just as we would expect from the north and south sides of a bar magnet.
So let’s imagine that a muon looks a little bit like a loop of current, which, in turn, looks a little bit like a bar magnet.
What’s the next step in developing this classical picture? Well, we’ve already claimed that currents cause magnetic fields. Our next step will be to argue that magnetic fields pull on currents, albeit in a funny sort of way.
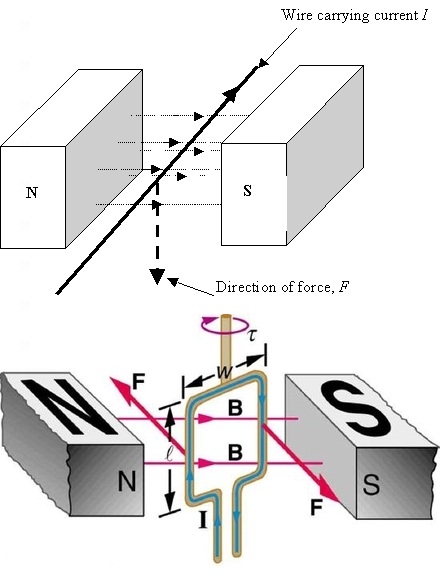
Magnetic forces are a little tough to understand because they push or pull in a direction that’s perpendicular both to the direction of the magnetic field and the direction of the current. This is shown in the top panel of Fig. 2. The magnetic field points from the north pole of one magnet to the south pole of another. The current is running away from us, through the wire, into the page. But the magnetic force is pulling the wire down. Were the current coming toward us, the magnetic force would be pushing it up.
This sort of perpendicular push-pull game from magnetic fields has an interesting effect when you put a loop of current in a constant magnetic field. For a current going around in a circle, the current travels in different directions on different sides of the loop. The magnetic force on opposite sides of the loop will point in different directions, and there will be zero total force on the loop. But this doesn’t mean that there is no effect. While the loop won’t accelerate up or down, these forces cause the loop to rotate.
The rotation of a current loop is pictured in the bottom panel of Fig. 2. This, incidentally, is also the principle behind a direct current motor.
How fast will our little loop of current wobble? That depends on a few different factors—some that we control, and others that we measure.
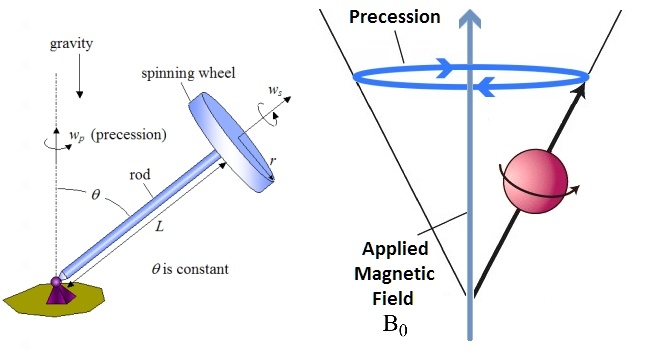
The analogy that physicists (including Chris Polly in the Fermilab seminar embedded above) like to use here is that of a gyroscope, or a toy top. The top spins about its axis at some rate, but it also precesses around its pivot at a different rate. The rate of precession depends on the ratio of the force of gravity pulling on the object to the rotational inertia of the object. The ratio of these two quantities determines the dynamics of its preccession.
A similar thing happens with spin. If we put our muon (which, remember, we’re imagining is like a little loop of current) in a big magnetic field, it will wobble around the direction of the applied field like a hula hoop. And the bigger the magnetic field is, the faster the muon will wobble.
Two more things, and we’ll be in a place where we can understand what the Muon g-2 experiment measures. One of these things I already mentioned, but then told you to ignore. This was about how the muon decays into other particles. There are some wrinkles to this process; for instance, moving particles appear to decay more slowly than particles at rest, due to relativistic time dilation. But for the purposes of this story, the important thing to recognize is that energy is conserved, so when muons decay into electrons, the energies of the electrons that emerge reflect the energies of the muons that produced them, at the moment of their decay.
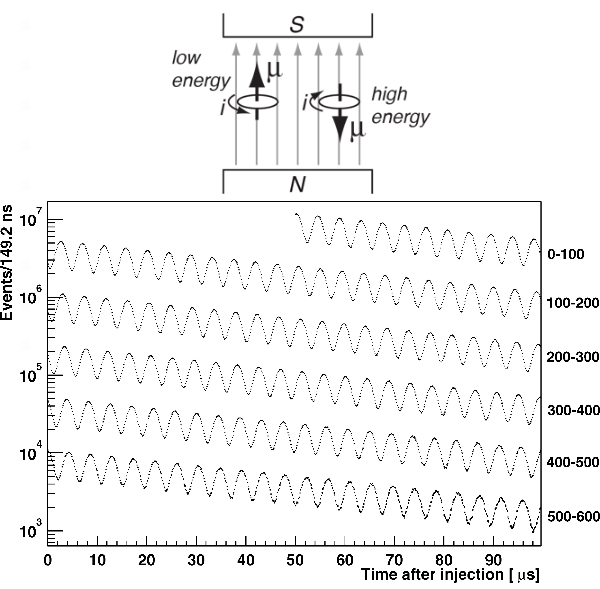
What does this have to do with our imaginary current loop? This is the other thing. The loop has different energies depending on its orientation relative to the magnetic field, as shown in the top cartoon in Fig. 4. So if our loop is wobbling, precessing like a top about the direction of the applied magnetic field, the muon’s energy will regularly increase and decrease, depending on how it is oriented relative to the magnetic field.
This is exactly what the experimenters see. The bottom plot in Fig. 4 shows the energies of electrons that were produced by decays from muons. (This is a figure from the Brookhaven version of the Muon g-2 experiment, but the Fermilab version is very similar.) Essentially, this oscillation shows how the muon spin precesses relative to the magnetic field, which is quantified via the muon’s magnetic dipole moment.
I’ve left some things out in this description, but it’s enough to tell you about the anomalous magnetic dipole moment of the muon. In terms of the current loop model, the magnitude of the magnetic dipole moment μ is the product of the current going around the loop and the loop’s area. This magnitude depends on things like the elementary charge (e, which is the same for the electron and the muon), the muon mass (m), Planck’s constant (ħ), and a convention, the g-factor:
μ = g (e/2m) (ħ/2).
Now, this factor out front, g, is approximately equal to 2. In fact, the Muon g-2 experiment has been exquisitely designed so that if g were precisely equal to two, the wobbles in Fig. 4 would disappear. Hence the idea of an anomalous magnetic moment. Physicists want to know just how much greater than zero the quantity g-2 is, as a way to test the standard model.
And this, dear reader, is where the professional journalists all started. Maybe they were wise to do so. As every young physics student learns, certain absurdities lurk in quantum analogies that are reified too ambitiously. The muon is not a loop of wire, even if it is sometimes helpful to imagine it as one. Many revolutions in physics (including, famously, Newton’s law of universal gravitation and Maxwell’s equations of electrodynamics) required their creators to leave old analogies behind.
Yet there are times when a simple story is more useful than a true story. Whether this sentence is a reasonable summary of the history of science, I leave for the philosophers to decide. Last week, I taught students to spin a cue ball with a magnet in its center, and when we applied a magnetic field to it, I was delighted to see the cue ball wobble, just as I had hoped.
