Siobhan Roberts in The New York Times:
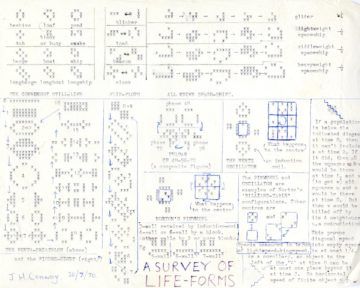In March of 1970, Martin Gardner opened a letter jammed with ideas for his Mathematical Games column in Scientific American. Sent by John Horton Conway, then a mathematician at the University of Cambridge, the letter ran 12 pages, typed hunt-and-peck style. Page 9 began with the heading “The game of life.” It described an elegant mathematical model of computation — a cellular automaton, a little machine, of sorts, with groups of cells that evolve from iteration to iteration, as a clock advances from one second to the next. Dr. Conway, who died in April, having spent the latter part of his career at Princeton, sometimes called Life a “no-player, never-ending game.” Mr. Gardner called it a “fantastic solitaire pastime.” The game was simple: Place any configuration of cells on a grid, then watch what transpires according to three rules that dictate how the system plays out.
Birth rule: An empty, or “dead,” cell with precisely three “live” neighbors (full cells) becomes live.
Death rule: A live cell with zero or one neighbors dies of isolation; a live cell with four or more neighbors dies of overcrowding.
Survival rule: A live cell with two or three neighbors remains alive.
With each iteration, some cells live, some die and “Life-forms” evolve, one generation to the next. Among the first creatures to emerge was the glider — a five-celled organism that moved across the grid with a diagonal wiggle and proved handy for transmitting information. It was discovered by a member of Dr. Conway’s research team, Richard Guy, in Cambridge, England. The glider gun, producing a steady stream of gliders, was discovered soon after by Bill Gosper, then at the Massachusetts Institute of Technology.
More here.