by Jonathan Kujawa

On December 22nd I started thinking about topics for this month’s 3QD essay. In a happy coincidence, someone posted to Twitter that Srinivasa Ramanujan was born on December 22, 1887. We’ve touched on Ramanujan’s work here at 3QD, but it seemed like a sign that we should dive a little deeper [0].
The story of Ramanujan is now famous, especially after the award-winning film “The Man Who Knew Infinity” [1]. He was born in southern India into a poor family. His talent in mathematics was noticed at an early age, but it wasn’t until he got hold of a copy of G. S. Carr’s “Synopsis of Pure and Applied Mathematics” at the age of fifteen that his talent was really revealed. Carr’s book was meant to be a Cliff Notes to undergraduate mathematics for students cramming for Cambridge University exams. It gave little to no explanations — just a thousand pages of raw, uncut mathematical formulae stated as gospel. Using Carr’s book, Ramanujan taught himself mathematics.
Ramanujan became consumed with his own mathematical explorations. So much so that he neglected his college studies and failed out after the first year. He continued to do math and live in poverty until his mother arranged for him to marry S. Janaki in 1909. Feeling the responsibility of marriage, Ramanujan eventually found employment as a clerk in the Madras Port Trust Office and in 1913, thanks to the encouragement of other mathematicians in India, finally sent a letter containing some of his results to several famous mathematicians in the UK.
Faithful 3QD readers might recognize the first of the following formulas from Ramanujan’s letter:
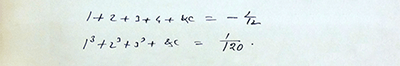
In one of my first essays for 3QD I talked about how you can make sense of infinite sums and how, properly interpreted, it is reasonable to think of the sum of all the counting numbers as equal to -1/12.
Now if you know about the Riemann zeta function and modern number theory, you’ll recognize all the correct mathematics buried beneath what seems to be raving nonsense. Fortunately for Ramanujan he sent his letter to G. H. Hardy. At the time Hardy was a world leader in number theory and was probably one of the few who knew enough to recognize Ramanujan’s genius.
I’m not famous, but I do get “crank letters” from time-to-time. Every mathematician with an email address gets unsolicited packets of someone’s hard-earned results. Exactly a year ago someone contacted me with the claim that they had figured out a method of using cycloids to predict the paths of tornados. I’m not an expert in cycloids or tornados, but that seemed like a stretch to me. I tried to be kind as I sent the person on their way to hopefully find someone who could better appreciate their work.
I try to give these sorts of emails a fair shake because of Ramanujan. As I said, he sent Hardy a lengthy letter containing page after page of mathematical results. Worse, they were presented in the Carr style of one fact after another without explanation or justification. Imagine getting this in the mail:
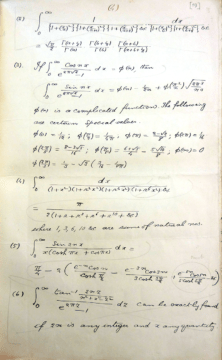
Despite his brief and difficult life, Ramanujan created entire worlds of new mathematics. After his death, he left three notebooks containing over 3000 different entries. These notebooks were written in the short span of ten years (1904 to 1914)!
In the 1920s two English mathematicians, Watson and Wilson, started the huge project of turning Ramanujan’s notebooks into publishable work with proofs and explanations added where needed. After more than a decade of work, their efforts petered out. It wasn’t until the 1980s and 1990s that Bruce Berndt at the University of Illinois enlisted the help of George Andrews at Penn State University along with various other mathematicians to finally complete the project. Altogether Berndt published a five-volume set containing the fleshed-out results of the three notebooks of Ramanujan.
Among mathematicians, however, there is an even more famous Ramanujan “notebook”. In 1976, George Andrews visited Cambridge University. He had heard there were papers from the estate of Watson about their early efforts to publish Ramanujan’s notebooks. Amazingly, in one of the boxes he found a hundred or so pages of mathematics in Ramanujan’s handwriting!
In the year before he died Ramanujan spent his days pushing his research further and recording the results he discovered. They were, of course, in the Carr style: statement after statement with few explanations provided. But to an expert like Andrews, they were an obvious goldmine of new mathematics! This bundle of notes became known as Ramanujan’s Lost Notebook.
As Berndt described it:
The discovery of this ‘Lost Notebook’ caused roughly as much stir in the mathematical world as the discovery of Beethoven’s tenth symphony would cause in the musical world.
Berndt and Andrews have devoted their entire careers to the mathematics of Ramanujan recorded in the notebooks. In addition to the aforementioned five-volume set, Berndt and Andrews have spent the last twenty years publishing an additional five volumes on just the mathematics of the Lost Notebook.
Indeed, just last year Berndt, Junxian Li, and Alexandru Zaharescu published a proof of the last remaining claim from the Lost Notebook. Namely, they proved the following identity:
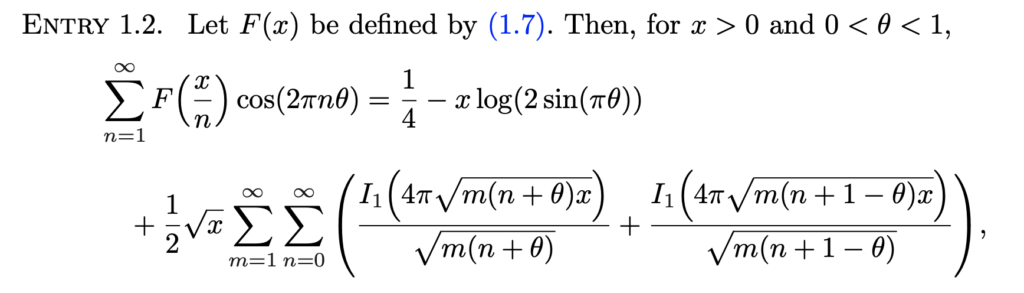
Here F(x) is either x-1/2 or the floor function of x, depending on if x is an integer or not, and I1 is a certain combination of Bessel functions. Suffice it to say, even understanding Ramanujan’s formula is not so easy!
Even now it is a mystery how he came up with his results. Sometimes Ramanujan credited the goddess Namagiri as the source of his ideas.
Recently John Baez asked Berndt if all of Ramanujan’s original claims have been proven or disproven [3]. Berndt replied:
To the best of my knowledge, there are no claims or conjectures remaining. There are some statements to which we have not been able to attach meaning.
Altogether it took a full century to verify the discoveries Ramanujan made in just over a decade. One can only imagine what he would have done with another thirty years!
It is a bit melancholic to know that Ramanujan’s claims have all been settled. As an undergraduate at Gustavus Adolphus College I remember reading about Ramanujan and marveling at his formulas [4]. Not only could I not prove them, I couldn’t even understand them. Nevermind discovering them in the first place!
On the other hand, mathematics is an immortal Hydra: every answer begets even more questions. Entire new fields of research were launched based on Ramanujan’s work and mathematicians in these areas are as active as ever. The Mock Theta functions introduced in the Lost Notebook by Ramanujan were only really understood after the 2001 Ph.D. thesis of Sander Zwegers. They’ve since become a vibrant area of research within Number Theory.
And we can always dream of a mathematical Indiana Jones discovering another Lost Notebook of Ramanujan!
[0] In a funny coincidence, while waiting for dinner to finish in the oven this evening, we watched the Futurama episode entitled “The Farnsworth Parabox”. The story involves multiple universes, and one of them is labeled “Universe 1729”. See here for why that made me laugh out loud.
[1] If you’d like to watch the film, it seems to be available here on Youtube.
[2] Image borrowed from here.
[3] See John Baez’s blog post here. This is where I first learned that Ramanujan’s last formula had finally been proven.
[4] It didn’t help that the math lounge had a prominently displayed bust of Ramanujan. Gustavus’s sculpter-in-residence, Paul Granlund, had been commissioned to make the bust and he gave his initial version to the math department. Talk about intimidating company!
