by Jonathan Kujawa
If you’d like a punch to the throat, use classroom hours as a measure of the work of the next teacher or professor you meet at a social event. It’s like only counting hours on the playing field for a professional athlete or hours in the air for a pilot.
There is hidden work in every job. For university faculty, a big part of their job is conducting research, publishing that work, and getting the grant funding needed to do that work. For both teachers and professors, there is also the mentoring of students outside the classroom. For university faculty, this frequently comes in the form of student research projects.
Many of my essays at 3QD have focused on the work of professional mathematicians, but there is a vibrant community of student
researchers, as well. Indeed, Involve is an entire journal devoted to publishing new research in mathematics suitable for publication in mainstream research journals, but with the extra requirement that at least 1/3 of the authors be undergraduate students. Full disclosure: my colleague, Mike Jablonski, is an editor at the journal.
Four years ago we talked about the work of my former student, Rhyker Benavidez. Rhyker worked on questions involving the symmetric group which were inspired by biology. I have worked with several students since then, but none have done projects which seemed suitable for a 3QD essay. On the other hand, my collaborator, Rob Muth, was just telling me about some great work done by students of his at Washington & Jefferson College. Rob was justifiably proud of their results and I thought they were perfect for the readership of 3QD.
The first group consisted of Daniel Florentino and Ethan Moy. They worked on the problem of sleepy museum watchmen. Imagine you have a polygonal-shaped museum (maybe designed by Frank Gehry). You need to locate the guard stations so that every point inside the museum is within eyesight of one of the guards. The question then is, how few guards do you need? Specifically, can you find upper and lower bounds on how many guards you might need?
This is a classic problem that has been around for nearly 50 years. In 1975 Chvátal proved that n/3 guards are always sufficient for a museum with n walls and, moreover, for some museums you can’t get by with fewer guards. The mark of an interesting math problem is if people pick it up and generalize to new scenarios.
In Chvátal’s setup, it is assumed the guards can watch in every possible direction, up to a full 360 degrees if needed. It is also assumed that the guards are ever vigilant and you don’t need any redundancy. But, if you go to the Louvre to see the Mona Lisa the guards aren’t twirling like a Mevlevi and your heist better not hinge on distracting only one guard. Subsequent mathematicians considered the problem under the extra restrictions of having guards limited to a 180 degree view, or requiring that each guard is in the line of sight of another guard (in case one should become sleepy, the other will notice and can sound the alert).
Daniel, Ethan, and Rob considered the problem under the requirement that both restrictions are in place. Guards can only look 180 degrees, and each one must be in the line of sight of at least one other guard. Here’s an example from their paper:
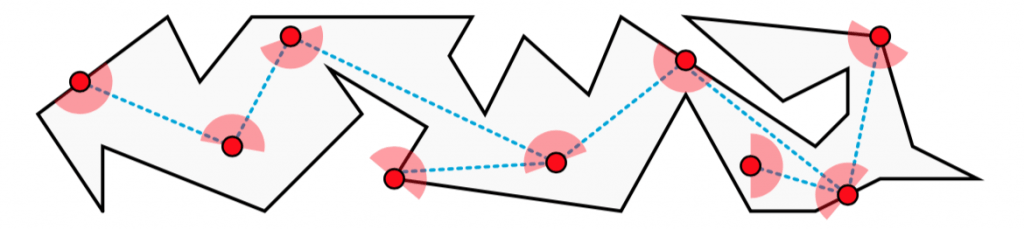
As you see, each guard (the red dots) has at most a 180 degree field of view, each is in view of another guard (the dashed blue lines), and all together they can monitor the entire museum.
They proved that in this situation n/2 – 1 guards is always sufficient and sometimes necessary. Notice that their result requires more guards than Chvátal (for example, if the museum has n=24 walls, Chvátal only needs 8 guards, while Daniel, Ethan, and Rob need 11 guards). That jives with our common sense: Daniel, Ethan, and Rob’s setup has more restrictions, so will need more guards to cover the museum. Or, to say the same thing differently, a solution given by Daniel, Ethan, and Rob is also a solution for Chvátal, and is probably overkill.
Not only do they figure out how many guards you need, their argument gives a procedure for how to position the guards. If the Met should like consulting on their guard placement, I’m sure Daniel, Ethan, and Rob would be happy to oblige! You can find their preprint here.
Of course, being math, their results involve only the salient aspects of the problem and, hence, can be applied in all sorts of situations. You could easily imagine NASA wanting to place sensors in a lunar crater or the National Park Service wanting to place sensors in the Grand Canyon. Moreover, those sensors may have a limited field of view and you might want the sensors to be able to communicate with a neighbor. That way they will form a mesh which allows data to be shared between sensors and to home base.
Heck, Daniel, Ethan, and Rob’s results could help in the design of minigolf courses!
The second group was Alexas Iams and Hannah Johnston. The problem they considered is a variant of the classic computer game Minesweeper. Millions of work hours have been frittered away playing it on Windows-based computers around the world. If you’d like to try it yourself, Minesweeper is built right into Google.
In the case of Alexas, Hannah, and Rob, they call their version the Quicksand Game. Imagine you would like to traverse the Fire Swamp and avoid the quicksand. They assume you have a certain number of stones. When you toss a stone it could land on solid ground. In this case, you know all the ground between you and the stone is solid and, moreover, you can walk over and pick up your stone to use it again. Otherwise, the stone lands on quicksand. In which case you know that all the ground beyond where the stone landed is quicksand and, moreover, your stone sinks and disappears and cannot be used again. Here is a picture from their paper illustrating the rules of the game, where the red wavy lines indicate the hidden quicksand, green is ground you now know is solid, and orange is ground you now know is quicksand:
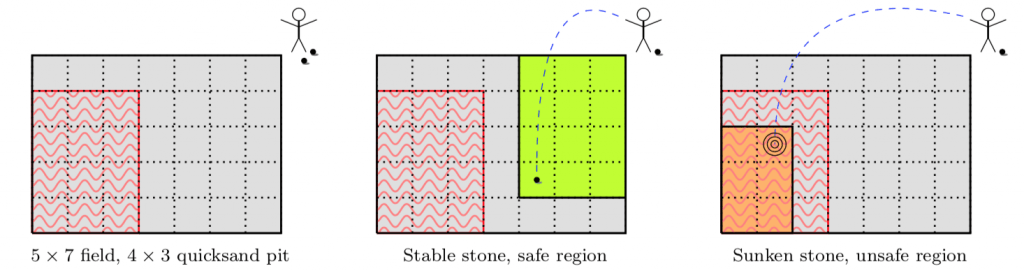
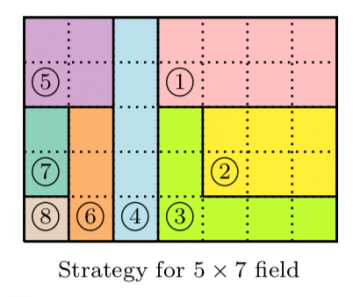
The question is, for a given rectangular field with a region of quicksand in the opposite corner, what upper and lower bounds can you give on the number of stones needed to determine the location of the quicksand? Alexas, Hannah, and Rob tell you exactly how many stones you need for any field which has a side no longer than 6 square units. Even better, they have a procedure that tells you exactly where to throw the stones. For example, in the 5 x 7 field from above a clever adventurer needs only two stones. Even better, they tell our adventurer that she should throw the stones in locations 1, 2, 3, 4, 5, 6, 7, 8 (in that order) in the map below:
In fact, Alexas, Hannah, and Rob do much more than this. They consider arbitrary partially ordered sets (that is, sets where you have notions of relative position), not just grids, and they obtain upper and lower bounds on the number of stones needed to detect the analogue of quicksand (what they call quicksand ideals).
They also show their upper and lower bounds cannot be improved in the sense that there are partially ordered sets that exactly need the minimums and maximums they computed. They give explicit formulas for these upper and lower bounds, but since they’re not super informative at first glance, I won’t post them here. Rob tells me their paper should be on the ArXiv preprint server soon if you’d like to see their formulas for yourself.
Once again, what starts as a trifle turns into a potentially useful tool. It’s not likely you’ll find yourself in the Fire Swamp, but you may well be interested in detecting pollution in a network of rivers. Imagine the Mississippi River system:
Now imagine you have a sampling device you can drop into the river. If the device signals it has detected pollution, then you want to retrieve the device with a full sample of river water to take back to the lab (and, hence, have used up that sampling device). On the other hand, if it signals no pollution, you can rinse it out and use it again later. How many sampling devices do you need to locate the source of the pollution? Alexas, Hannah, and Rob’s results tell you the answer!
Once you start looking, you can find all sorts of scenarios where their sampling algorithms could be useful.
The third group is Dina Abbasian, Lena Difulvio, Gabrielle Pasternak, Isabella Sholtes, and Frances Sinclair. They do some really cool work on things called cuspidal ribbon tableaux. These are Tetris-like pieces which can be fit together according to certain rules. They are interesting to research mathematicians thanks to their connection to the Specht modules for the Khovanov- Lauda-Rouquier algebra of affine type A. These are a hot area of research these days and their results will no doubt be of interest to experts. Unfortunately, it’s a bit technical to explain here. And, I must admit, even though I do research in related areas, it will take me a while to absorb what all they’ve done. Instead, I’ll show you some pretty pictures of puzzles which can be made with cuspidal ribbon tableaux:
If you’d like to see the details, Rob tells me their paper should be on the ArXiv preprint server soon.
[1] Image from Wikipedia: By Shannon – Background and river course data from here, CC BY-SA 4.0, see here.