by Jeroen Bouterse
 I have some very simple New Year’s resolutions, and some that require an entire column to spell out. One example of the latter is that I want to make a subtle but meaningful change in how I talk to my (middle and high school) math students about proofs.
I have some very simple New Year’s resolutions, and some that require an entire column to spell out. One example of the latter is that I want to make a subtle but meaningful change in how I talk to my (middle and high school) math students about proofs.
First, I need to be open about the fact that talking about proof in mathematics comes with an especially strong impostor syndrome: as a secondary school teacher, who am I to talk about the nature and limits of deductive reasoning in a discipline of which I have barely scratched the surface? I know high school proofs of high school mathematical concepts; I am vaguely aware that people much cleverer than I have tried to reduce all mathematical claims to analytical (logical) truths, or at least to a limited set of axioms; and I believe that after having mentioned this, I have to name-drop Gödel as the person who has supposedly put a stop to these projects, even though I have never studied his incompleteness theorem and doubt I would be able accurately to judge its relevance and meaning. That’s about it.
Usually, doubts like these are something to keep hidden in a light-hearted column like this, because they waste space and look self-absorbed. In this case, however, I think they are relevant, because I suspect I will not be the only one who (1) is by no means an expert on mathematical logic, and (2) still has some intuitive convictions about the special relation between mathematics and provability. Most of us, when we think about mathematics and proof, think of high school or undergraduate mathematics. I think it is fair to say that this is the most culturally prominent face of mathematics: the concepts almost all of us have been taught, or at least heard about, and the discourses surrounding the teaching of those concepts.
These discourses will depend in part on the teachers you have encountered, but I’ll go out on a limb here and speculate that most mathematics teachers will have told most of their classes, at some point, that “in mathematics we believe things because we can prove them”. I know I have made comments in that spirit. I have also come to feel a bit uncomfortable about them. Let me tell you why.
Proving and trusting
Classroom contexts in which these chirpy remarks naturally come to me are usually those occasions in which I have given two or three examples of a concept or theorem in practice, and then moved on to show with some algebraic or geometric magic that it actually works for all cases of a certain kind.
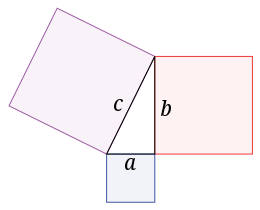
In a classroom proof, say of the Pythagorean theorem, a lot of things come together. One is simply the experience of demonstrating something. Another is the apparent jump to the infinite: we can show that given any right triangle, Pythagoras’ theorem holds. In one sentence, we can say something about an infinite number of triangles. A third is the practical implication that whenever the conditions of our demonstration are met (which, for instance, involves a diagram with triangles with sides of lengths a, b, c in a square with sides of lengths a + b), we are allowed to use the theorem.
It’s good that a lot of interesting stuff happens at the same time. It’s also potentially confusing. My first worry is that maybe I am guilty of mystification, by exaggerating the miraculousness of this particular miracle we have just witnessed. Though it feels to me as if we have genuinely demonstrated something amazing, it may be fairer to say that what we have done is rewrite some algebraic expressions encoding some of our assumptions about spatial relations – assumptions most of which remain, in this classroom context and in the minds of those involved, implicit and non-rigorous. Why should I dance around yelling excitedly to my students that we have performed magic today, when I might equally well say, in a suitably monotone voice, that we have done some good bookkeeping today that will serve us well in our later bookkeeping efforts?
My second worry concerns the message that the proof is why we are allowed to believe and apply the theorem. I’m afraid this message is misleading, for we haven’t actually arranged the curriculum so that students are allowed to work only with what they have proven. After fussing about how important this proof of the Pythagorean theorem is, I will cheerfully go on to say that from now on, we will assume that the Pythagorean theorem works in right triangles, and only in right triangles. That last clause is affirming the consequent; we haven’t demonstrated this. I will, true to the temporary spirit of rigor and truthfulness, solemnly admit to my students that we haven’t. I will also move on to what the textbook and I have harmoniously decided to be more interesting stuff: to the Pythagorean theorem in 3D shapes – no proofs involved.
Critical-minded though some of my students are (I am fondly and proudly thinking of some in particular who will reliably raise their hand whenever I make a quick general statement about prime factorization, and remind the class that what the teacher just said does not apply to the number 1), none of them has ever stopped me here and confronted me with the promises implied by my brief but moving “believing things because of proofs”-speech. This is a relief and a cause for hope that I have not yet done irreversible damage. For of course I don’t expect my students to believe only what we have proven. Honestly, I expect them to believe what I say because I say it.
I mean that behind my authority as a teacher is an implicit promise that if we roughly do things ‘my way’, they will, all in all, keep making sense. Students’ trust in their mathematics curriculum is social. I mean this not in the sense that they mindlessly absorb falsehoods just because they are in the textbook – they will in fact notice typing errors in the algebra sections. I mean that even though maybe they secretly aren’t able to fully grasp this proof yet and it doesn’t in their heart of hearts actually make sense to them that you can say something about the sides of triangles by looking at squares and juggling around with letters, they know people have apparently done this and worse before and survived. That they didn’t find a gap in the proof is of little consequence; what matters is that they approach the exercises in this chapter with the expectation that what they have just been taught will help them get the required results.
In time, of course, and through conscious efforts both on their part and on mine, we hope these things will make sense, in the sense that new techniques involving Pythagoras’ theorem come to be tied not just to my local expectations, but to their background knowledge and their existing skills. The point is that the role of proofs here is decidedly modest, and that this is not a defect in high school mathematics; rather, the defect is in the idea that a successful proof should be typical of the entire range of activities that make up mathematical practice.
It is all too easy to take the experience of establishing a compelling proof, and generalize this experience to the whole subject. In doing so, we are overselling ourselves. Not because of fundamental logical subtleties like Incompleteness, as these subtleties usually do not directly touch the phenomenology of high-school mathematics. Rather, we are overselling ourselves because we are claiming that the combination of rigor and certitude we were able to achieve in this case is typical of all mathematical practice. As philosopher of science Ian Hacking said, “only dogma or theory has made people say that mathematics as a whole has a peculiar certainty.”[1]
Norms and ideology
At this point you may object: maybe rigor isn’t typical of everything students experience in mathematical education; however, isn’t it typical of the norms professional mathematicians face; of what is required for extending the boundaries of mathematics? And doesn’t it make sense for us to inject some academic ethics into the classroom context, not all the time but sometimes? In history classes, we don’t cite primary sources to every claim we make; but doesn’t it make sense to say, every now and then, that ‘as historians’ we ought ‘of course’ to believe historical claims only on the basis of primary sources?
I’d reply that no, I don’t believe that these foundationalist maxims have a place either in mathematics or in history classes. If we are so keen on connecting the academy to the classroom, on giving students a ‘taste’ of what would be involved in contributing to a field, then I’m much more in favor of giving them a taste of the complexities, ambiguities and uncertainties involved than in feeding them philosophical myths.
The misleading part of these myths is not that sources are central to history, or that proofs are central to mathematics. The misleading part lies in the suggestion of absoluteness. Primary sources are not in any absolute sense an end-point to historical inquiry; they are the thing that historians keep circling back to, relating them as best they can to the knowledge, theories and debates of the day and their own informed judgments. It is no doubt possible to construct a normatively positivist philosophy of history that seeks to absolutize the status of primary sources, but it is unlikely that the language and practices required by such a philosophy would be reflected in the best available historiography. Likewise, proofs are important in mathematics, but they are neither where mathematicians start thinking nor where they stop.
The grain of truth in our clichés does not justify those clichés. When we simplify “proof plays an important role in mathematics” to “mathematicians believe things only if they are proven” and do so invoking a naïve concept of proof as something that provides absolute certainty, the concept of proof comes to bear a burden too heavy for a secondary school subject.
Too heavy, and too risky. For the cultural notion of mathematics’ special relation to absolute certainty tends to be connected to a rather straightforward historical narrative, in which the culture that established this special relation was the ancient Hellenic world, usually in its role as precursor of the modern West. Long story short: when I sing the praises of deductive proofs, I need to be aware of the role popular and scholarly conceptions of proofs have played in perpetuating mythologies of essential Western intellectual superiority.[2]
I will sing those praises still. None of what I have said here is meant to detract from how amazing mathematics is, and how deep and interesting the mathematics that students encounter in middle and high school. This bears emphasizing, because I know from experience that humanistic inclinations to search for and point out the complexities, particularities, the local judgments and negotiations involved in culturally important sciences are often seen as attempts at undermining those sciences. Or that taking an interest in the problematic aspects of the history of a culturally important idea is intended to smear this idea.
I am not a skeptic about mathematics, and not a pessimist or a cynic about its cultural relevance. I just think the question of what practices characterize or distinguish different subjects and fields in the sciences and humanities is one to which the honest answers are very complex, and the easy answers are ideologically charged. For that reason, I will think twice before I start preaching about the essence of mathematics, or making absolute claims about the norms of the subject that don’t connect to my actual classroom expectations.
The day this column gets published on 3quarksdaily, I will start working towards an understanding of Pythagoras’ theorem with a new cohort of students. As I do every year at this point, I will tell them what a privilege it is to introduce them to it. When we get to the theorem itself, we will have a go at proving it. We will do so because the activity of proving something, or even of attempting to prove something, has a part to play in increasing our understanding of what we are claiming or doing with this theorem.
Proofs as an activity
This notion, that the activity of trying to demonstrate something will itself lead to interesting new perspectives, has a respectable philosophical pedigree. In the famous dialogue between Socrates and the slave boy in Plato’s Meno, where the two set out to double the area of a square, the boy’s first conjecture is that doubling the lengths of the sides will double the area of the square. Only when the attempt to make this work fails and the boy is properly confused does Socrates start to nudge him towards a construction that actually doubles the area of the original square.[3]
Both the failed and the successful demonstration serve the goal of increasing understanding: in the first case, by showing that our implicit intuitions were inconsistent; in the second case, by providing us with more coherent insight. The demonstrations, by the way, are based in both cases not on manipulating variables but on manipulating specific numbers (“2 feet”, “4 feet”) in a way that can be extended to other numbers.
A similar, albeit more sophisticated example of an idealized classroom discussion about proofs can be found in Imre Lakatos’ Proofs and Refutations. In this dialogue, the teacher sets out, with a group of students, to prove a theorem (Euler’s formula describing the relations between the number of edges, vertices and faces of polyhedra, though the precise formulation of the theorem will evolve in the course of the dialogue). Their attempts lead to an exciting dialectic of attempted demonstrations, counterexamples, and adaptations or reformulations of the claim to be proved. While some students are focused mainly upon the question whether the proof has accomplished what it set out to do, and how we can ever be certain that no new kind of “monsters” or counterexamples will turn up from unexpected corners, the teacher is much more relaxed about these questions, musing: “You are interested only in proofs which ‘prove’ what they have set out to prove. I am interested in proofs even if they do not accomplish their intended task.”[4]
Lakatos’ dialogue proves the teacher’s point: at the end, you may feel confident that the final and best formulations of Euler’s formula are true, proven and certain; but your confidence may also be shaken by the bumpy road that got you there. However, what you can be confident about is that the whole journey has improved your understanding of the theorem. The teacher will still bring this aspect of proofs into focus – and the students in Lakatos’ dialogue are also clearly prepared to philosophize about the scope and meaning of proofs. In this case, however, their narration draws attention to what is going on in the classroom – in the dialogue – rather than pontificating about what is or ought to be going on in all of mathematics.
I like that better.
[1] Ian Hacking, ‘What mathematics has done to some and only some philosophers’, Proceedings of the British Academy 103 (2002) 83-138: 98.
[2] For examples, see Chemla(2012), Karine, ‘Historiography and history of mathematical proof: a research programme’ in: Karine Chemla ed., The history of mathematical proof in ancient traditions (Cambridge University Press).
[3] Plato, Meno, from 82f.
[4] Imre Lakatos, Imre, Proof and refutations. The logic of mathematical discovery. John Worrall, Elie Zahar ed. (1976; this edition Cambridge University Press, 2015) 15.
