Alessandra Vespignani in Nature:
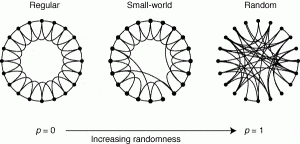In 1998, Watts and Strogatz1 introduced the ‘small-world’ model of networks, which describes the clustering and short separations of nodes found in many real-life networks. I still vividly remember the discussion I had with fellow statistical physicists at the time: the model was seen as sort of interesting, but seemed to be merely an exotic departure from the regular, lattice-like network structures we were used to. But the more the paper was assimilated by scientists from different fields, the more it became clear that it had deep implications for our understanding of dynamic behaviour and phase transitions in real-world phenomena ranging from contagion processes to information diffusion. It soon became apparent that the paper had ushered in a new era of research that would lead to the establishment of network science as a multidisciplinary field.
Before Watts and Strogatz published their paper, the archetypical network-generation algorithms were based on construction processes such as those described by the Erdös–Rényi model2. These processes are characterized by a lack of knowledge of the principles that guide the creation of connections (edges) between nodes in networks, and make the simple assumption that pairs of nodes can be connected at random with a given connection probability. Such a process generates random networks, in which the average path length between any two nodes in the network — measured as the smallest number of edges needed to connect the nodes — scales as the logarithm of the total number of nodes. In other words, randomness is sufficient to explain the small-world phenomenon popularized as ‘six degrees of separation’3,4: the idea that everyone in the world is connected to everyone else through a chain of, at most, six mutual acquaintances.
However, random construction fell short of capturing the local cliquishness of nodes observed in real-world networks.
More here.