 Late on a rainy night some years ago, a few blocks away from home on Broadway, I happened to give a homeless man a dollar or two. In gratitude, he handed me a book. It was very dark, so I had to wait until I got home to see that it was a wet, worn and torn, pale blue copy of Studies in Mathematics, Volume XI: Mathematical Methods in Science by George Polya, edited by Leon Bowden. Leaving it to dry on the radiator overnight, I looked at it the next day. It turned out to be a course of lectures that Polya had given in the summer of 1962 at Stanford to high school teachers of mathematics, under the auspices of the National Science Foundation. (Confession: the book has a Hunter College stamp in it, which may mean that I am in posession of a purloined library book.)
Late on a rainy night some years ago, a few blocks away from home on Broadway, I happened to give a homeless man a dollar or two. In gratitude, he handed me a book. It was very dark, so I had to wait until I got home to see that it was a wet, worn and torn, pale blue copy of Studies in Mathematics, Volume XI: Mathematical Methods in Science by George Polya, edited by Leon Bowden. Leaving it to dry on the radiator overnight, I looked at it the next day. It turned out to be a course of lectures that Polya had given in the summer of 1962 at Stanford to high school teachers of mathematics, under the auspices of the National Science Foundation. (Confession: the book has a Hunter College stamp in it, which may mean that I am in posession of a purloined library book.)
 As I skimmed through the book, I found much fascinating material, but most of all, I was struck by a short introduction to the work of Simon Stevinus. I had never heard of Stevinus before this, and I would guess that many of you might not have either. It turns out that Stevinus was a brilliant 16th century Dutch mathematician, engineer, and scientist; a contemporary of Decartes, who even anticipated some of Galileo’s work. Stevinus was the first to use decimal fractions and showed their usefullness. As an engineer, he constructed dykes which are in use to this day.
As I skimmed through the book, I found much fascinating material, but most of all, I was struck by a short introduction to the work of Simon Stevinus. I had never heard of Stevinus before this, and I would guess that many of you might not have either. It turns out that Stevinus was a brilliant 16th century Dutch mathematician, engineer, and scientist; a contemporary of Decartes, who even anticipated some of Galileo’s work. Stevinus was the first to use decimal fractions and showed their usefullness. As an engineer, he constructed dykes which are in use to this day.
What I want to talk about today is this: contrary to popular caricature, science does not always advance by observation and measurement. Often, it is a simple thought experiment which results in new insight. Einstein’s musings about what would happen if he sped along with a wave of light at a speed close to its own resulted in a rather famous conclusion, for example. (Of course, even Einstein’s thinking was connected to reality by the experimental and observational work of others.) And this serendipitously-discovered book exposed to me a truly marvelous thought experiment I hadn’t ever known about. I would like to explain this physically-intuitive proof in some detail to you, by which Stevinus derived the Law of Inclined Planes. In going through this step-by-step, I hope to illustrate the power of the thought experiment in general, and the elegance of Stevinus’s imaginative formulation in particular.
Now bear with me here: it is obvious that pushing an object up an inclined plane is easier than lifting it up vertically. (The weight of an object is simply the force required to lift it up vertically.) This is why a brewer will load his wagon by rolling casks of beer up a ramp, and it is pretty obvious that the steeper the ramp, the harder it is to roll the casks. The closer the ramp becomes to vertical, the closer the force required to roll (lift) the cask up becomes to its actual weight. But what exactly is the force required to roll a cask up a given inclined plane? This is the question that Stevinus set out to answer.
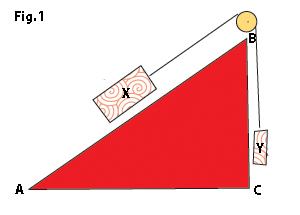 His first important move was to ask the question in a clear way. He realized that he must simplify the situation so that only the relevant physical quantities come into play, so he decided to ignore friction (something all of us are now used to doing from high school physics!). Deciding what is relevant and what isn’t is, in fact, half the job. This is how he put it: given the setup of inclined plane and pulley in Fig. 1, what weight would Y have to be, to balance X and keep it from sliding up or down the plane? Keep in mind that movement of X on the plane is frictionless (or you can imagine that the weight X has little wheels that allow it to roll on the plane), as is the pulley.
His first important move was to ask the question in a clear way. He realized that he must simplify the situation so that only the relevant physical quantities come into play, so he decided to ignore friction (something all of us are now used to doing from high school physics!). Deciding what is relevant and what isn’t is, in fact, half the job. This is how he put it: given the setup of inclined plane and pulley in Fig. 1, what weight would Y have to be, to balance X and keep it from sliding up or down the plane? Keep in mind that movement of X on the plane is frictionless (or you can imagine that the weight X has little wheels that allow it to roll on the plane), as is the pulley.
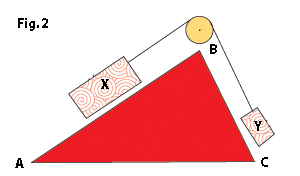 Stevinus’s next move was to realize that the vertical drop is just a special (extreme) case of another inclined plane, so he was able to generalize his question to this one: given the new setup in Fig. 2, once again, what weight does Y have to be, to balance X and keep it from sliding up or down the plane? (This time, imagine Y as also having little wheels, so it can slide up or down its own inclined plane without friction.)
Stevinus’s next move was to realize that the vertical drop is just a special (extreme) case of another inclined plane, so he was able to generalize his question to this one: given the new setup in Fig. 2, once again, what weight does Y have to be, to balance X and keep it from sliding up or down the plane? (This time, imagine Y as also having little wheels, so it can slide up or down its own inclined plane without friction.)
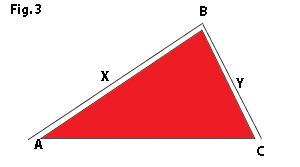 Stevinus realized that the shape of the weights X and Y is irrelevant, and in an extraordinary leap of imagination, he replaced them with just a uniform rope (or chain). This situation is shown in Fig. 3. Assuming that the rope can still slide without friction on the inclined planes, it is clear that if the downward force is greater on the segment AB, then the rope will slide down that plane. If the downward force is greater on the segment BC, then the rope will slide down that side, and if the forces are in equilibrium, then the rope will stay balanced as it is. So which is it?
Stevinus realized that the shape of the weights X and Y is irrelevant, and in an extraordinary leap of imagination, he replaced them with just a uniform rope (or chain). This situation is shown in Fig. 3. Assuming that the rope can still slide without friction on the inclined planes, it is clear that if the downward force is greater on the segment AB, then the rope will slide down that plane. If the downward force is greater on the segment BC, then the rope will slide down that side, and if the forces are in equilibrium, then the rope will stay balanced as it is. So which is it?
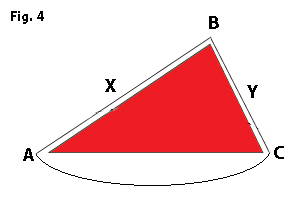 Again, in a brilliant move, Stevinus imagines the two ends of the rope connected by an additional loose length of rope. So now we have a closed loop of rope draped over the inclined planes. The situation now looks as shown in Fig. 4. We can see that although the situation is asymmetrical above the line segment AC, it is the same on both sides (the A side and the C side) below it, where the rope simply hangs in a symmetrical U-ish shape (called a catenary, and while we are on the subject see also this). Whatever forces the rope below AC exerts on the part of the rope above AC, must therefore be the same at A and at C. (The part of the rope below pulls equally on both sides.) So now the startling conclusion: if the part of the rope above AC, on the inclined planes, were to tend to slide down to one side, this would result in perpetual motion in that direction! (Because as it slides down a little bit, an equal part of the rope which had been hanging below would go up the inclined plane on the other side, and the situation would be identical to what we started with, therefore more of the rope would slide down, and it would just keep going like that forever.) We will have constructed a pertpetual motion machine. Since this cannot be right, Stevinus concluded that the parts of the rope above AC on the inclined planes must also be in equilibrium. Since X and Y are in equilibrium, and we also know that the weight of the rope is proportional to its length, this means that at equilibrium, the ratio of the weights X/Y justs equals the ratio of the lengths AB/BC. This finally answers our initial question from Fig. 2: What weight does Y have to be, to balance X and keep it from sliding up or down the plane? Simple algebraic manipulation shows that since X/Y = AB/BC,
Again, in a brilliant move, Stevinus imagines the two ends of the rope connected by an additional loose length of rope. So now we have a closed loop of rope draped over the inclined planes. The situation now looks as shown in Fig. 4. We can see that although the situation is asymmetrical above the line segment AC, it is the same on both sides (the A side and the C side) below it, where the rope simply hangs in a symmetrical U-ish shape (called a catenary, and while we are on the subject see also this). Whatever forces the rope below AC exerts on the part of the rope above AC, must therefore be the same at A and at C. (The part of the rope below pulls equally on both sides.) So now the startling conclusion: if the part of the rope above AC, on the inclined planes, were to tend to slide down to one side, this would result in perpetual motion in that direction! (Because as it slides down a little bit, an equal part of the rope which had been hanging below would go up the inclined plane on the other side, and the situation would be identical to what we started with, therefore more of the rope would slide down, and it would just keep going like that forever.) We will have constructed a pertpetual motion machine. Since this cannot be right, Stevinus concluded that the parts of the rope above AC on the inclined planes must also be in equilibrium. Since X and Y are in equilibrium, and we also know that the weight of the rope is proportional to its length, this means that at equilibrium, the ratio of the weights X/Y justs equals the ratio of the lengths AB/BC. This finally answers our initial question from Fig. 2: What weight does Y have to be, to balance X and keep it from sliding up or down the plane? Simple algebraic manipulation shows that since X/Y = AB/BC,
Y = X * BC / AB — and this is the Law of Inclined Planes
And there you have it! The weight needed at Y will always be as much less than X, as the length of the side it is resting on is less than the length of the other side. If BC is only half the length that AB is, then only half the weight of X will be needed at Y to balance it. And this conclusion holds no matter what the actual inclinations are, because we have (or Stevinus has) derived this result generally, without specifying any particular angles of inclination. In other words, the law will hold even for the vertical case of Fig. 1. (If you still don’t get it, you could try the explanation here.) I find this a very beautiful result, especially as it relies on extraordinary imagination guided by good intuition at each step. In addition, the proof exploits considerations of symmetry, which were to become of paramount importance in 20th century physics, through the connection of symmetries with conservation laws.
 For all his work with inclined planes, even Galileo’s reputation as an experimenter is probably exaggerated. For example, it is unlikely that Galileo bothered to drop objects of different weights from the Tower of Pisa to show that they fall at the same rate. He was too smart to have needed to do this, and had his own thought experiment to show that objects of different weights must fall at the same rate: imagine that you have two objects, say iron balls, one of which weighs 20 pounds and the other 5 pounds. Now, it was thought that the 20 pound ball falls faster (say at some rate F) than the 5 pound one (which falls at a slower rate S). Imagine connecting the two balls with a chain, then dropping them. What will happen? Well, presumably the 20 pound ball should pull the lighter object into a faster rate than S, while the lighter ball should slow down the 20 pound ball from its fast rate of F. In other words, joined together, the balls should drop at some intermediate rate between S and F. But now consider that the two balls joined by a chain can also be construed as one object with a weight of 25 pounds, which should fall even faster than the heavier ball alone, or faster than F! Here we have a contradiction, so they must fall at the same rate. Such is the beauty of the thought experiment!
For all his work with inclined planes, even Galileo’s reputation as an experimenter is probably exaggerated. For example, it is unlikely that Galileo bothered to drop objects of different weights from the Tower of Pisa to show that they fall at the same rate. He was too smart to have needed to do this, and had his own thought experiment to show that objects of different weights must fall at the same rate: imagine that you have two objects, say iron balls, one of which weighs 20 pounds and the other 5 pounds. Now, it was thought that the 20 pound ball falls faster (say at some rate F) than the 5 pound one (which falls at a slower rate S). Imagine connecting the two balls with a chain, then dropping them. What will happen? Well, presumably the 20 pound ball should pull the lighter object into a faster rate than S, while the lighter ball should slow down the 20 pound ball from its fast rate of F. In other words, joined together, the balls should drop at some intermediate rate between S and F. But now consider that the two balls joined by a chain can also be construed as one object with a weight of 25 pounds, which should fall even faster than the heavier ball alone, or faster than F! Here we have a contradiction, so they must fall at the same rate. Such is the beauty of the thought experiment!
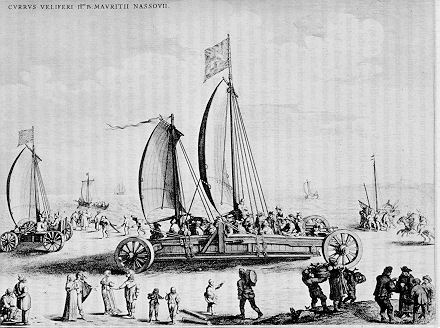 Stevinus is even supposed to have proven that objects of different weights fall at the same rate before Galileo did. He did work in hydrostatics, noting that the pressure exerted by a liquid depends only on its height and is independent of the shape of the vessel containing it. He also invented a sail-powered carriage which could outrun horse-drawn vehicles of the time, shown here in the picture. He was quite a guy.
Stevinus is even supposed to have proven that objects of different weights fall at the same rate before Galileo did. He did work in hydrostatics, noting that the pressure exerted by a liquid depends only on its height and is independent of the shape of the vessel containing it. He also invented a sail-powered carriage which could outrun horse-drawn vehicles of the time, shown here in the picture. He was quite a guy.
Thanks to Margit Oberrauch for doing all the inclined plane illustrations.
Have a good week!
