Ben Orlin in Science News:
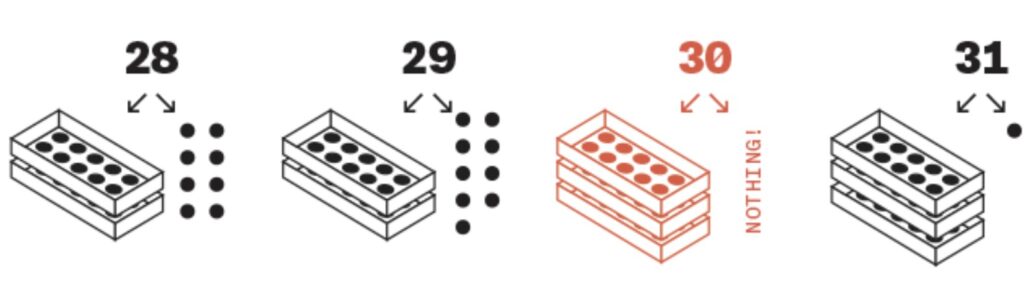
Here, count with me: 1, 2, 3, 4, 5, 6, 7, 8, 9, T, 11, 12 … Oh, what’s that? You write ten with “zero”? Fair enough. Zero, we have been told, is the foundation of our number system. Mathematician Tobias Dantzig once called it “a development without which the progress of modern science, industry or commerce is inconceivable.” But that changed in 1947, when mathematician James Foster laid out a system that works like ours in every way — except that it lacks nothing. He called it “a number system without a zero-symbol.”
Think of our familiar system as a series of boxes. You can leave up to nine loose objects unboxed. But if a tenth object arrives, you must pack the ten into a box. When this happens, we use zero to denote an absence of loose objects. The numeral 30 means three boxes of ten, and no additional objects.
This principle continues. For example, in 407, the zero signifies that there are no loose tens; they’ve all been boxed up as hundreds.
More here.
Enjoying the content on 3QD? Help keep us going by donating now.
