By cosmos I mean “the universe as seen as a well-ordered whole.” It thus stands in opposition to chaos. By metaphysical I mean…well, that’s what I’m trying to figure out. Wikipedia tells me that it is one of the four main branches of philosophy, along with epistemology, ethics, and logic and “the first principles of: being or existence, identity and change, space and time, cause and effect, necessity, and possibility.” Well, OK.
Perhaps I’m thinking something like: It is through metaphysics that chaos is ordered into cosmos. I rather like that. I doubt that they’ll buy it in Philosophy 101, but then this isn’t Philosophy 101. It is rather stranger and, perhaps, more interesting.
We’ll see.
Grasping the Cosmos: Powers of Ten, Fantasia
Let’s start with the physical universe. Back in 1977 Charles and Ray Eames toured the known universe in a nine-minute film called Powers of Ten. The film starts with an aerial view of a couple sitting on a blanket in a Chicago park at the shore of Lake Michigan. The field of view measures one meter. Then we zoom out by powers of ten, 10 meters, 100 meters, 1000 meters and so forth. As we zoom out voice-over narration explains what’s we’re seeing until the field of view measures 10^24 meter (100 million light years). We zoom back, very quickly, the voice-over pointing out that some regions are empty while others are populated. Once we reach the point where we started the field of view narrows to the man’s hand, and then every smaller until, at 10^-16 we’re viewing quarks. Note that almost all of the interesting visual action is between 10^9 and 10^-9 meters. Outside that range we see dots.
That’s just a sample of the physical world. You might want to take a couple of minutes to think of some things that are missing from the video. No mountains, nor fish, sewing machines, cattle, trees, lightning strikes, violins, hail, nor asteroids, cruise vessels, nebulae, coral reefs, plankton, squid, and on and on and on. Thing upon thing, all physical beings.
But Powers of Ten hasn’t been the only modern attempt to visualize the universe. In 1941 Walt Disney released Fantasia which, in the course of presenting classical music to middle America, also envisioned the world, though not with the austere and rigorous vision of the Eameses. In the episode, Rite of Spring, Disney presented the evolution of life on earth from its origins through the extinction of the dinosaurs. The spatial scale ranged from a point outside the solar system down to individual cells undergoing mitosis, not as wide as that in Powers of Ten, but arguably wider than anyone had previously presented within the compass of half an hour, not to mention the temporal compression involved in whizzing through 4 billion years of evolutionary history.
Another episode in Fantasia presented a more intense visualization of the physical world. The Nutcracker Suite envisioned a small plot of woodlands, measured in feet or yards, over the course of a year. Taken together these two episodes presented the natural world as it had never been seen.
Taken together these two films, Powers of Ten and Fantasia, present the physical world in a way that is at one and the same time is woefully incomplete and yet that aspires to indicate the whole. In doing so they necessarily impose some kind of order on the world. That imposition is what I am calling metaphysics.
What must a world be that its structure is learnable?
This metaphysics inheres in the relationship between us, homo sapiens sapiens, and the world around us. It is because of this metaphysical structure that the world intelligible to us. What is the world that it is perceptible, that we can move around in it in a coherent fashion? Whatever it is, since humans did not arise de novo, that metaphysical structure must necessarily extend through the animal kingdom and, who knows, plants as well.
Imagine, in a crude analogy, that the world consists entirely of elliptically shaped objects. Some are perfectly circular, others only nearly circular. Still others seem almost flattened into lines. And we have everything in between.
In this world things beneficial to us are a random selection from the full population of possible elliptical beings, and the same with things dangerous to us. Thus there are no simple and obvious perceptual cues that separate good things from bad things. A very good elliptical being may differ from a very bad being in a very minor way, difficult to detect. Living in such a world would be somewhere between difficult and impossible because it would be necessary to devote enormous time and energy to make the finest of distinctions. One mistake, and you’re dead. Mistakes would be inevitable.
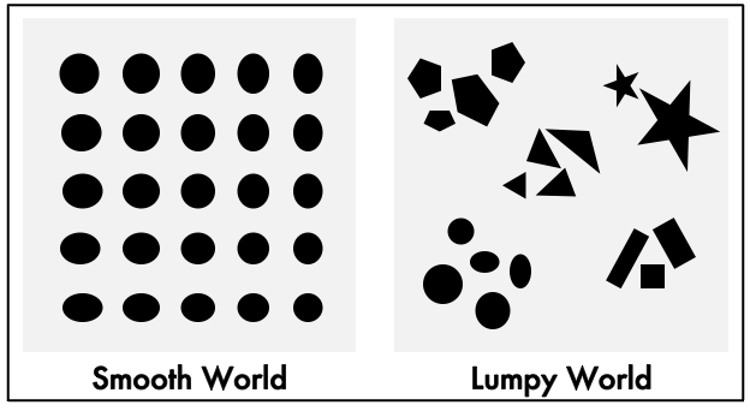
Call that a smooth world (to the left in the figure), where smoothness is understood to be metaphysical in character rather than physical. A smooth world would be all but impossible to live in because the things in it are poorly distinguishable. Ours is a lumpy world, but in a metaphysical sense rather than a physical sense. Things have a wide variety of distinctly different (metaphysical) shapes and come in many different sizes. In a lumpy world quick and dirty cognitive processes would allow us to make reliable distinctions.
Referring back to Powers of Ten, the universe above the scale of 10^10 meters and below the scale of 10^-10 meters is smooth in this sense. The region in which we live, roughly 10^7 to 10^-7 is dense with lumpiness.
Now, imagine an abstract space in which objects are arranged according to their metaphysical “shape” or “conformation”. In a smooth world all the objects are concentrated in a single compact region in the space because they are pretty much alike. In a lumpy world objects are distributed in clumps throughout the space. Each clump consists of objects having similar metaphysical conformations but the clumps are relatively far apart because objects belonging to different clumps resemble one another more than any of them resembles an object in another clump.
Referring back to the diagram, objects in the smooth world are differentiated along two (physical) dimensions, call them height and width. We can easily imagine a third dimension, orientation (rotation), giving us a cube of ellipsoids. The lumpy world has five clusters of objects. The objects within each cluster can be differentiated along two or three, perhaps, four dimensions for each cluster. But how do we differentiate among the clusters? What dimensions do we need for that?
We live in a lumpy world. Yes, there are cases where small differences are critical. But they don’t dominate. Our world is intelligible. Plants are distinctly different from animals, tigers from mice, oaks from petunias, rocks and water are not at all alike, and so on. It is this lumpiness that makes it possible to construct a conceptual system capable of navigating in the external world so as to preserve and even enhance the integrity of the internal milieu. Learnability depends on lumpiness. And what is learned is the structure of that lumpiness.
The world’s learnability is not something that can be characterized in a reductionist fashion. Whatever it is that makes, for example, a trail in the forest learnable, cannot be characterized simply in terms of the chemical structure of things in the forest, or their mechanical properties. Learnability can only be characterized in relation to something that is learning. In particular, for us, a central aspect of the world’s metaphysical structure lies in the correspondence between language and the world.
“This is most peculiar,” you might remark. “Tell me again, how does this metaphysical structure of the world differ from the world’s physical structure?” I will say, provisionally, that it is a matter of intension rather than extension. Extensionally the physical and the metaphysical are one and the same. But intensionally, they are different. We think about them in different terms. We ask different things of them. They have different conceptual affordances. The physical world is meaningless; it is simply there. It is in the metaphysical world that we seek meaning.
Text as the interplay of the world and the mind
Text reflects this learnable, this metaphysical, structure, albeit at some remove. AI learning engines are modeling structure inherent in text after text after text for millions if not billions of texts. That structure exists because it was written by people engaged with and making sense of the world as they wrote.
If those people had been spinning out language in a random fashion there would be no structure in the text for the engine to learn, no matter how much such text it traversed. The structure thus learned is not, however, explicit in the statistical model created by the engine, as it would be in the operations of a “classical” propositional/symbolic model of the kind investigated back in the 1970s and 1980s. You can’t ‘open up’ one of these models and read their internal structure. They are thus said to be opaque or unintelligible.
We might think of these models as hyperobjects in the sense defined by Timothy Morton. He has defined them as “things that are massively distributed in time and space relative to humans” (Hyperobjects, p. 1). The Anthropocene is his prototypical example of a hyperobject. The era of anthropogenic climate change is physically massive.
But a large language model is not physical at all, or is it? That’s a tricky question, very tricky. It takes a large computing system to create such models, large in the sense that computational systems can be large, lots of memory, lots of CPUs (central processing units) and GPUs (graphic processing units). But the physical system is not the model, no more (and no less) than brains are identical the ideas that reside within them. Rather than continuing on and attempting to adjudicate the issue, I’ll rest content with the assertion that these models are easily among the largest and most complex informatic objects humankind has created. That makes them hyperobjects.
Let us return to learnability. There are two things in play: 1) the fact that the text is learnable, and 2) that it is learnable by a statistical process. How are these two related?
If we already had a rich and robust explicit symbolic model in computable form, then we wouldn’t need statistical learning at all. Statistical learning is a substitute for the lack of a usable propositional model. The statistical model does work, but at the expense of explicitness.
But why does the statistical model work at all? That’s the question. It’s not enough to say, because the world itself is learnable. That’s true for the propositional model as well. Both work because the world is learnable.
Description, narration, computation, and time
The human mind involves both statistical and propositional processes. It is the propositional engine that allows us to produce language. A corpus is a product of the linguistic activity of a propositional engine which is, however, coupled to perceptual systems that have a statistical aspect. And those perceptual systems are essential to the process of navigating the lumpiness that is the physical world.
Description is one basic linguistic action; narration is another. Analysis and explanation are perhaps more sophisticated and depend on (logically) prior description and narration. Note that this process of rendering thought into language is inherently and necessarily temporal. The order in which signifiers (word forms) are placed into the speech stream depends in some way, not necessarily obvious, on the relations among the correlative signifieds (roughly, ‘meanings’) in an abstract semantic or cognitive space. Those relations are a first order approximation to the lumpiness of the world. Relative positions and distances between signifiers in the speech stream reflect distances between and relative orientations among correlative signifieds in that semantic space. We thus have systematic relationships between positions and distances of signifiers or word forms in the speech stream, on the one hand, and positions and distances of signifieds in semantic space. It is those systematic relationships that allow statistical analysis of the speech stream to reconstruct semantic space.
The statistical analysis of the speech stream is thus a second order approximation to the lumpiness of the world as it is apprehended by the statistical operations of perceptual systems. It is a shadow of, a simulacrum of, the metaphysical structure of the world.
Large Language Models as Digital Wilderness
I think those who see ourselves on the brink of AGI (artificial general intelligence) are fooling themselves. Whatever AGI is, we’re no where near it. To see GPT-4 as putting us on the brink of inventing artificial minds of great depth and power is to misoverestimate – to parody a coinage by George W. Bush – what we have in these strange and wonderful hyperobjects.
Yes, there is a sense in which the whole world is there, as, in a somewhat different sense, the whole world is implied by Powers of Ten and Fantasia. To get it all there in one ‘place,’ that is an achievement of considerable power. That is worth thinking about, worth contemplating. But that sense is convoluted and indirect.
I like to think of large language models as digital wilderness, to be explored and mapped. That is to say, we will investigate and come to understand them so that they no longer seem opaque. I see this as a process that will require decades. We’ve hardly even begun this process.
It’s time to begin exploring, to begin making sense of the metaphysical structure of the cosmos.
