by Jochen Szangolies

Picture the internet circa late 2000s, during the heyday of New Atheism: virtually everywhere, it seemed, people were embroiled in a grand crusade for truth, a final showdown of faith versus reason, religion versus science, revelation versus empiricism. On both sides, fallacy was the weapon of choice: demonstrate the logical error at the heart of your opponent’s argument—burn down their straw men, chase the true Scotsmen from their hiding spots, poison the cherries they pick—and add a notch to your belt.
These were simpler times, where truth was a monolithical concept, not the many-fingered, complex thing it has become, where universal principles reigned superior over context and individual perspective, where all of the crummy details of human life seemed just so much detritus to abstract away to find the common truth below—a truth that, you were sure, everybody would be compelled to accept, could they just manage to see past their various biases and prejudices. This vision has receded into the mist—and, one might say, good riddance: how much richer is the world in all its variety, where different perspectives cannot all be resolved into a grand, but bland homogeneity, but must find a means of peaceful coexistence, where the individual is no longer neglected in favor of the supposedly universal, where we each might have a chance to live our truth. But let’s not get ahead of ourselves.
An Error Of Consequence
It is not my purpose here to review the merits, or the lack thereof, of New Atheism-style discourse, nor do I wish to pass judgment on today’s. But, while fallacy man may have hung up his cape (and hat), there is one lesson that is worth taking to heart, even today—one of the simplest examples of fallacious reasoning that nevertheless seems nearly unparalleled in its deleterious effect. This is the fallacy of affirming the consequent—an inversion of logic that takes a valid inference and invalidly infers its converse.
Its fallacious nature is readily apparent: from ‘I was out in the rain, therefore I am wet’, it does not follow that the observation ‘I am wet’ licenses the conclusion ‘therefore, I was out in the rain’. I could be wet for all manner of different reasons. Yet, somewhat astonishingly, awareness of its fallacious nature seems to do little to curb its prevalence.
A part of the reason may be that, in a world of uncertainty, it can often present as a good heuristic—if you’re reasonably sure that there are no good alternative explanations, then having been out in the rain might be the best explanation for my wetness. In this form, as ‘inference to the best explanation’ or abductive reasoning, it may in fact be an invaluable element of a reasoner’s toolkit, allowing us to navigate everyday uncertainty as well as serving as the basis for scientific hypothesis formulation.
But this should not blunt our appreciation of the destructive potential of blithely affirming the consequent. Consider the following: a rich person may buy themselves a nice house, a flashy car, and other various external signifiers of their wealth.
Now take a person of more average means. Living within those means, none of the trappings of wealth will accumulate around them: they might rent a modest apartment, drive an aging car, and so on. Suppose that, one day, they find their money spent at the end of the month—but find that they can just continue spending: beyond the number shown on their account turning negative, nothing much seems to happen. They seem to have found a cheat code to wealth: now, each month, they end up spending more than they have, to buy some nicer things. Indeed, they find that they can replicate this trick along different modalities: they max out various credit cards, take out loans, and so on, thus racking up an ever more impressive burden of debt. Outwardly, their life may show all the signs of increased wealth—but of course, the inversion of the above proposition does not hold: great wealth may lead to a high standard of living, but a high standard of living does not necessarily imply great wealth. Just take the case of Anna Sorokin, inspiration for the Netflix series Inventing Anna, as an example.

This may all seem rather obvious. Yet, it is exactly the type of logic behind the argument that the course of human history is one of overall progress—as championed, for example, by rationalist and New Atheism holdout Steven Pinker. We’ve collectively never had it so good, the argument goes, so we must be doing something right. As Pinker puts it:
“Human flourishing has been enhanced in measure after measure, and I wanted to tell the broader story of progress, and also to explain the reasons. The answer, I suggest, is an embrace of the ideals of the Enlightenment: that through knowledge, reason, and science we can enhance human flourishing—if we set that as our goal.”
But this falls into the same trap as those that bought Anna Sorokin’s story of the wealthy heiress (who’s just right now somewhat strapped for cash) did—after all, how else could she support her lifestyle, if not by being wealthy?
So, what does explain our—undeniable—global increase in living standards, if not the essential rightness of the dominant (and by that, largely Western) paradigm of ‘knowledge, reason, and science’? Just as in the story above, it’s debt. We are able to afford our lifestyles simply by going deeper and deeper into debt each year. (Obviously, this neglects the gross disparities in lifestyle between different countries.) Globally, in 2022, we exhausted the resources available to us on July 28—and all ‘wealth’ generated beyond that is effectively borrowed against the future habitability of Earth. So, just a little more than half of what we spend is backed by what we have—the rest is a loan taken out against the future.
This has obviously grave consequences. Buying into Pinker’s line of reasoning, we might conclude that the system that got us this far can’t be so bad, after all—and continue living large on the expense of a future that looks more dire with every further year of inaction. What we should instead conclude is that in order to become truly wealthy, as opposed to accumulating the trappings of wealth by racking up an ever-growing mountain of debt, we desperately need to learn to live within our means. Thus, one of the simplest possible errors of reason goes a ways to explaining just why we fail to show the planet we live on the kindness we’re expected to show a public toilet—to leave it in the condition we would hope to find it.
Of Targets And Measures
But things don’t stop there. After all, wealth, or even a wealthy lifestyle, isn’t an end in itself. What we want is, instead, to flourish: to live happy, comfortable, and meaningful lives. The trouble with this is that it’s a difficult thing to measure. So, suppose you’re in the shoes of a hypothetical policy maker aiming to improve overall life satisfaction: how do you know whether the policies you implement actually fulfill their goal of increasing life satisfaction, if you have no tools to measure it directly?
A common statistical tool applied in such situations is to look for a proxy: a quantity that is correlated with the one you want to know about, but is more readily measurable. Thus, if you find a variable that increases or decreases with, say, mean life satisfaction per capita, or something like that, then you can instead observe the variations of its value as a gauge of the success of your decisions.
For life satisfaction, a good candidate proxy seems to be wealth: on average, wealthier people are more satisfied with their lives (up to a point). And wealth is a readily measurable quantity; consequently, one might resolve that policies that increase average wealth are policies that increase average well-being. Now, note that, again, this is a relationship of the basic form ‘if A, then B’: a higher life satisfaction is found to go along with greater wealth. But again, the inverse fails to hold: it’s perfectly well possible to be wealthy, but miserable.
Hence, the proxy and the quantity it supposedly tracks can come apart: without an independent means to ensure the correlation, policies may optimize the proxy at the expense of the tracked quantity. This example of fallacious reasoning differs slightly from the simple affirmation of the consequent, because the relation between a quantity and its supposed proxy may not be a logically necessary one, but it is recognizably of the same family, which we might call ‘fallacies of inversion’—believing a relationship that holds in one direction to hold also in the other.
Another pertinent example is that of citation numbers in academic publishing: generally, good research is cited more often. Consequently, measures are put into place that reward being highly cited—such as access to funding or highly prestigious positions.
But then, as soon as those measures are in place, the quality of research itself ceases to be a relevant goal—if you can publish crap, but have it cited often, you reap the same benefits as those publishing good research; and, on the assumption that crap is produced more easily, this may, in fact, yield a competitive advantage. Thus, it becomes the de facto optimal strategy to quickly produce lots of crap: the policies intended to reward good research end up having the opposite result.
Of course, this is somewhat exaggerated for effect. There are safeguards in place to try and curb this sort of behavior, to greater or lesser success. But the general principle remains: as encapsulated in the form of Goodhart’s law, named after the British economist Charles Goodhart, “when a measure becomes a target, it ceases to be a good measure”.
Many naive policy interventions are, upon closer inspection, of this sort: good, even admirable intentions, doomed by fallacious reasoning. It is related to the concept of perverse incentive: setting up rewards such that the optimal strategy reaping the most of them is one running counter to the original intention of the reward. The classic example is when the British colonial government of India, to curb the number of cobras in Delhi, offered up a bounty for every slain snake; as a result, people began breeding cobras, which, after the rewards program was scrapped in consequence, were released into the wild, increasing the total population. The British government may have—for once—had solely the well-being of the people in mind, but the implemented measures ended up making things worse.
Thus, inversion fallacies may not simply deceive us into thinking that a goal is reached, when in fact, it isn’t, as in the example of going into debt to appear rich—they may even cause us to follow the wrong goal in the first place.
Probabilities In Profile
The relationship between a quantity and its proxy is not generally one of strict implication: rather, changes in one quantity may be reflected in the other only with a certain probability. That is, the probability we ascribe to B may be increased, if we know that A obtains. Suppose you have two cookie jars, a red one and a blue one. In the red jar, 80% of the cookies are dipped in chocolate, while only 50% of those in the blue jar are chocolate-dipped. If you now know that you have the red jar, your chances of getting a chocolate cookie are markedly increased—but still, far from certain. Hence, having the red jar does not strictly imply that you’ll get a chocolate cookie, but it does increase the likelihood to do so. (I take it as axiomatic that chocolate-dipped cookies are objectively preferable.)
But now, suppose you are handed a chocolate cookie: what should you guess—that it came from the red, or from the blue jar? The likelihood of drawing a chocolate cookie is higher from the red jar, so it would be seductive to argue that it must probably have come from there. But suppose there are only 10 cookies in the red jar, while there are 100 in the blue one: then, 8 of the total 58 chocolate cookies came from the red jar, while the remaining 50 came from the blue one.
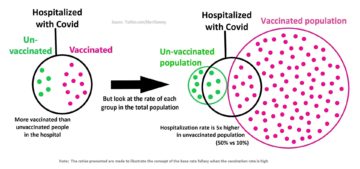
In this form, the illegitimate inversion of the relationship between two events is known as the base rate fallacy, because it neglects to take the overall background distribution of those events into account. This particular fallacy has done heavy duty in recent years in the narrative of vaccination skeptics and Covid-hoaxers: breathless posts on social media proclaimed that, because more people being hospitalized with Covid are vaccinated than unvaccinated, vaccinations are in fact harmful. But the reason is simply that the pool of the vaccinated is much greater, so a smaller proportion of the vaccinated being hospitalized ends up as a larger proportion of the hospitalized being vaccinated.
A flip side of this is the false-positive ‘paradox’. If 1% of a population is afflicted, you have a test that detects 72% of afflicted correctly, and identifies non-afflicted people with a probability of 99%, then if you have a positive test result, the probability that you actually are afflicted is only 50% (you can play around with the numbers here).
However, this sort of error has an even greater social implication. For one, this is the sort of logic behind racial profiling: if most terrorists are of a particular ethnicity, then the members of that ethnicity are more likely to be terrorists. Thus, such measures are not just morally abhorrent, but also, simply logically erroneous. Likewise with the identification of criminals using facial recognition: even a 99% effective system scanning thousands of people each day might condemn far more falsely categorized innocents than correctly identified criminals.
In this form, such inverted thinking has a yet more pernicious character. Suppose that, as a matter of statistical regularity, members of a certain population, perhaps characterized by a certain ethnicity, gender, class, or sexual orientation, show a particular trait. We are then just an inversion and a confusion of ‘is’ with ‘ought’ away from believing that those who show that particular trait ought to be members of that population—that is, from stereotyping and discrimination.
This particular inversion then leads to the codification of statistical regularities in the form of norms—of ways people ought to be or behave. Importantly, the salient question is not whether these regularities actually exist—whether there is such a thing as, say, ‘masculine’ behavior—but inverting such regularities as encompassing the only ‘right and proper’ way for things to be. It is then also this inversion—not primarily the question of the underlying regularity—where efforts to eradicate this form of hurtful stereotyping should most effectively attack. Difference and distinction is not itself bad, but only made bad by making them the basis of normative judgments.
Inversion fallacies are some of the simplest ways our reasoning can go wrong. When presented with explicit examples, few if any would fail to spot the simple logical error they represent. Yet, upon closer inspection, both our private and public lives are shot through with their consequences: from mistaken praise heaped upon ruinous economic systems to vaccine skepticism to bias and prejudice.
There’s no easy answer to this, and no straightforward conclusion to draw. But that’s perhaps how things ought to be: after all, it’s the reliance on the easy answer that simply takes the known and turns it around that’s gotten us to this point.
