by Jochen Szangolies
The world is a noisy place. No, I don’t mean the racket the neighbor’s kids are making in the back yard. Rather, I mean that, whatever you encounter in the world, probably isn’t exactly what’s actually there.
Let me explain. Suppose you’re fixing yourself a nice cocktail to enjoy on the porch in the sun (if those kids ever quiet down, that is). The recipe calls for 50 ml of vodka. You’re probably not going to measure out the exact amount drop by drop with a volumetric pipette; rather, maybe you use a measuring cup, or if you’ve got some experience (or this isn’t your first), you might just eyeball it.
But this will introduce unavoidable variations: you might pour a dash too much, or too little. Each such variation means that this particular Moscow Mule differs from the one before, and the one after—each is a slight variation on the ‘Moscow Mule’-theme. Recognizably the same, yet slightly different.
This difference is what is meant by ‘noise’: statistical variations in the measured value of a quantity due to inescapable limits to precision. For most everyday cases, noise matters comparatively little; but if you overshoot too much, your Mule might pack more kick than intended, and either just taste worse, or even make you yell at those pesky kids for harshing your mellow.
Thus, noise can have real-world consequences. Moreover, virtually everything is noisy: not just simple estimations of measurable quantities, like volumes, sizes, or time spans, but also less easily quantifiable items, like decisions or judgments. The latter is the topic of Noise: A Flaw in Human Judgment, the new book by economy Nobel laureate Daniel Kahnemann, together with legal scholar Cass Sunstein and strategy expert Olivier Sibony. The book contains many striking examples of how noisy judgment leads to wide variance in fields like criminal sentencing, college admissions, or job recruitment. Thus, whether you get the job or go to jail might come down to little more than random variation, in extreme cases.
But noise has another effect that, I want to argue, can shed some light on why so many people seem to hold weird beliefs: it can make the correct explanation seem ill-suited to the evidence, and thus, favor an incorrect one that appears to fit better. Let’s look at a simple example.
Truth And Fit
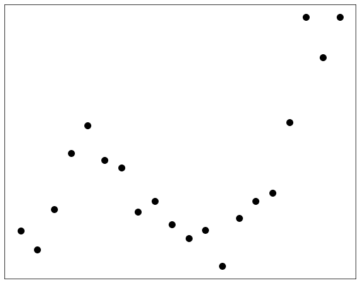
Consider the data in Fig. 2. For present purposes, it’s not important what those little specks are supposed to represent—only that they stand for certain observations (quantities, behaviors, verbal reports, results of actions…). What we’re looking for is an explanation for our observations. Given such an explanation, we can then make predictions—and if we’re right, reap the rewards.
It’s clear that there is some regularity to their distribution, but it might not be immediately obvious what the exact regularity is. Thus, we can produce different hypotheses and see how well they fit. If, for instance, a certain behavior coincided with the reception of food, an organism might hypothesize that this behavior was responsible for obtaining the reward, and engage in it more frequently. This is how we get superstitious pigeons.
This is the central problem any organism navigating a complex environment is faced with: observe, theorize, predict—if all goes well, the prediction comes to pass, and it gets the tasty morsel/evades the predator/impresses the potential mate.
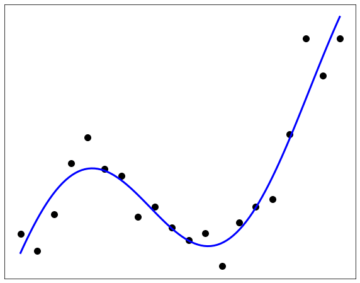
But sometimes, all goes not well. Suppose that the ground truth behind the data above is the curve in Fig. 3. Not all data points are on the line—some stray away quite far, in fact. This is the effect of noise: sometimes, the data we observe and the truth behind them don’t seem to agree.
In such a case, one might be tempted to seek for a ‘better’ model—find a hypothesis that better accounts for all the data. Such a model can, in principle, always be found—one merely has to increase the complexity.
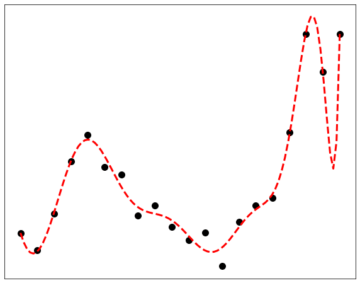
Consider the model in Fig. 4: on the whole, it is a much better fit for the data—almost every point lies very close to the curve. However, it is actually worse than the one in Fig. 3! It takes into account features of the data that are just due to natural statistical variation—i.e. noise—and accepts them as being part of the signal.
Yet still, it is not at all obvious in what way this model is worse. In fact, somebody proposing such a model might justifiably argue that it does a better job at reproducing the data, and hence, consider it superior!
When Occam Doesn’t Cut It
Now, one might be tempted to settle the dispute by appeal to Occam’s Razor, the time-honored principle that simpler explanations are typically better—more accurately, that one should not posit more explanatory entities than necessary. In a model like this, the ‘explanatory entities’ are the parameters—variable values—that go into its specification: more parameters makes for a more complex model; and with enough parameters, almost anything can be ‘explained’. As the Hungarian polymath John von Neumann put it: “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
But there’s a catch: while the Razor is straightforward enough in adjudicating between two hypotheses that account equally well for the data, in this case, one does an objectively better job—and since we can’t know a priori which one is actually right, excluding one just because it is complicated isn’t warranted. The world, after all, might just be that complicated!
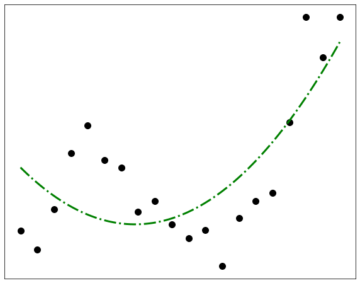
Furthermore, once we admit the possibility of accepting a worse fit to the data in the name of simplicity, it isn’t at all obvious anymore where we should stop. After all, we can always go simpler, if we accept the fit to the data just getting a little bit worse. Consider the model in Fig. 5: it is certainly the simplest one we have considered—and it still does fit the data to some extent.
Fine, then: if we can’t exclude either hypothesis on principle, we must see how well they do their job—that is, whether the predictions they make match future observations. After all, the proof is in the proverbial pudding: the reason we hypothesize in the first place is so that we can predict.
And here, we may be off to a promising start: the two models make wildly different predictions for some cases. Just consider the big dip to the right of Fig. 4, entirely absent in Fig. 3: if we could probe this behavior, then the score would be settled.
However, in addition to being noisy, real-world data is generally also incomplete. We seldom get the luxury of being able to do controlled, repeatable experiments in whatever way we are interested in. Suppose our model was intended to explain the behavior of the government, given its public actions—laws proposed and passed, regulations formulated, taxes imposed, and the like. If the two models then differ on what happens in secrecy, behind closed doors—say, boring committee meetings by fallible human beings versus dictates passed on down from a secret shadow world government of lizard people—we may simply not be free to collect the data necessary to adjudicate between the models.
What this demonstrates is that creating such ‘over-complicated’ models that strike others as ‘weird’ beliefs—i.e. conspiracy theories—does not stem from stupidity, nor ignorance. In fact, creating these models might be itself a task requiring prodigious intellectual resources!
If anything is at fault, it is a sort of lacking tolerance to noise—wanting the perfect explanation that reproduces all the data. This seems to be borne out by the typical reaction of those subscribing to such a model: when met with the suggestion that the weird light in the sky might just have been a plane, protestations follow that demonstrate a lack of fit of the hypothesis to the data: it was way too fast, its maneuvering too nimble, to be any Earthly craft.
The plane hypothesis is simple, but seems lacking, given the data; the UFO theory, on the other hand, fits the data perfectly—at the cost of introducing a spacefaring intelligence capable of crossing the vast distances between the stars, yet incautious enough to be spotted by the unaided eye. A greater tolerance to noise, an awareness that sometimes, things don’t quite make sense—that, in fact, we should expect things to not quite make sense, owing to the noisy nature of the world—might then be an adequate antidote for weird beliefs.
Nature Pulls A Magic Trick
We’re all aware of situations in which things don’t make sense. In fact, we sometimes seek them out, just to be amazed—and yet, we are unperturbed in our belief that there is a perfectly mundane explanation. This is the case with stage magic: typically, when met with the craft of a skillful performer, we, the audience, have absolutely no idea of how what we’ve just seen might work. And yet, few if any take that as a reason to believe in magic—the hypothesis fitting all the data by means of postulating all manner of mysterious entities—ghosts, demons, sprites—and powers—levitation, mind reading, precognition, and the like.
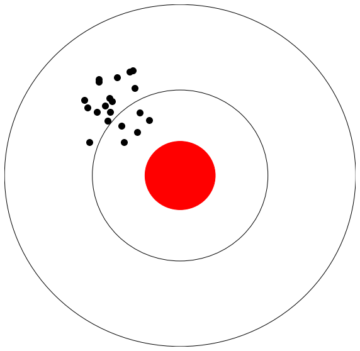
Why is that the case? Obviously, context matters: in the context of a magic show, we expect the data to lie—or better, to be manipulated, by sleight of hand and misdirection. In the context of stage magic, the data aren’t noisy—or not just—but rather, biased: tailored to produce a false impression.
Since we’re aware of the bias in this case, the way the data is manipulated to suggest the hypothesis that the magician has read our mind to discover the card we (believe we) have drawn at random from a stack, we are apparently less susceptible to believe complicated hypotheses in good accordance with the data.
Perhaps, then, we should think of nature (in a wide sense, as the world around us) as an accidental magician: every so often, by pure chance, noisy data aligns to give the appearance of bias, to suggest a more complex interpretation, replicating the magician’s most vaunted skill by sheer happenstance. We need to develop a greater tolerance to noise—to be OK with things not lining up, not quite making sense. In a noisy world, things should on occasion—and perhaps, quite often—not quite line up.
So in the end, a guiding maxim to hypothesis formation should be, don’t attribute to conspiracy what can equally well be explained by random chance—by noise, by things lining up just so. Neither simplicity nor explanatory power on its own suffices to guide our theorizing; the truth, we should expect, lies at a happy medium of complexity and fit.
We are often quick to assert a lack of intellectual capacities in those holding weird beliefs about secret societies, aliens, vaccines and the like. Believers thus often come to feel ostracized, ridiculed, or simply not taken seriously. This produces a ‘circle the wagons’-effect, with the ostracized seeking out like-minded communities more supportive of their ideas. As a result, the necessary social dialogue ceases, or is greatly impeded (for more on this sort of ‘social clustering’, see this previous essay).
If the above is correct, however, formation of such ‘weird beliefs’ is not due to any lack of intellectual capacity, but rather, due to an overemphasis of model fit, as opposed to model simplicity—or conversely, a lack of tolerance towards noise. Trying to get believers to revise their views by educational interventions then may not be the most promising approach. A better approach might be to instead improve noise tolerance.
Unfortunately, unlike in, say, training a machine learning model, we don’t have direct access to the parameters governing another’s theorizing. If your friend or family member starts posting about how Paul McCartney died in the late sixties and was replaced by an actor, there’s no handy knob you can turn to tweak their noise tolerance.
Perhaps, then, it is better to investigate what might be the cause of low noise tolerance. An obvious possibility here would be the need for certainty in an uncertain world: our hard-wired need to explain the world in order to predict it is continually thwarted by its sheer complexity. Thus, uncertainty—noise—is inherently threatening, and its elimination fosters a sense of security—at the expense of introducing a spuriously complex model. This suggests that finding a replacement source of security might foster a greater tolerance for noise—a thicker skin against the world’s inherent chaos, so to speak.
In order to prevent people falling prey to conspiratorial reasoning, then, it might be more effective to reassure their sense of security than to confront them with conflicting facts (thus ultimately just underscoring the complexity of the world, which might go some ways toward explaining the notorious backfire effect). Indeed, this seems somewhat supported by research linking belief in conspiracy theories with a search for certainty and that an increase in well-being can serve to inoculate against such belief.
A better strategy to reconnect with loved ones showing signs of conspiratorial belief than trying to ‘educate’ them out of it then might be to instead emphasize whatever fosters a sense of security in them—strengthen a relationship, reducing external stress, or just spending a bit of quality time with them (perhaps enjoy a magic show?).
This is unlikely to be a panacea, of course. Deeply entrenched conspiracy theory beliefs are difficult, and in some cases perhaps impossible, to redress. But it is important to keep in mind that the believer just follows a deeply human need for security and certainty in an uncertain, ‘noisy’ world. In that sense, there is no divide between ‘them’ and ‘us’—they are us, and we are them. Everyone has fallen for one of nature’s magic tricks at some point.
That doesn’t mean we should just hug it out with those propagating conspiratorial beliefs. Such beliefs can be harmful in a variety of ways, as for instance in the case where an Austrian doctor was driven to suicide after being targeted by the COVID-antivax crowd. Thus, such beliefs should be rationally opposed at every opportunity, if for no other reason than the benefit of the innocent bystander without settled views on the matter encountering it for the first time.
But the above does advocate for a change of state towards such thinking, and those that have succumbed to it. To see it as a maladaptive coping strategy in an increasingly complex world, rather than a lapse of reasoning. We must all sit together at the table, in the end.
